图形学笔记（四）变换——三维变换（三维旋转与欧拉角）、MVP变换、视图变换、投影变换（正交投影与透视投影）

图形学笔记（三）变换——缩放、镜像、切变
图形学笔记（五）光栅化——屏幕、像素、屏幕空间、视口变换、基础图元与三角形、采样、包围盒、锯齿或走样

1 三维空间中的变换

1.1 三维空间中的齐次坐标

与二维空间相似，有以下结论：

(x,y,z,w)在三维空间中表示的点：

1.2 三维空间中的变换

三维空间中齐次坐标的仿射变换矩阵(4*4)：

注意以上矩阵表示先线性变换，再平移。

三维空间中的缩放和平移：

1.2 三维旋转

1.2.1 绕固定轴旋转

在三维空间中，描述任意的旋转是不容易的。

所以我们以绕x轴旋转为例，观察上图，我们发现旋转过程中：

1. x是不变的，所以可以得到变换矩阵的第一个行向量(1,0,0,0)。
2. 然后对y和z进行$\alpha$的旋转得到第二个行向量$(0,\cos \alpha ,-\sin \alpha ,0)$和第三个行向量$(0,\sin \alpha ,\cos \alpha ,0)$。

最后的旋转矩阵$R_x(\alpha )$如下所示（同时也给出了$R_y(\alpha )$、$R_z(\alpha )$）：

上图中也可以看到，绕z轴旋转的推导过程和结果与x大致相同。

扫描二维码关注公众号，回复： 13464741 查看本文章

但是对于绕y轴旋转，由于$x\times z=-y$，所以要将$-\alpha$代入旋转矩阵的对应位置才会得到结果。所以绕y轴旋转的$R_y(\alpha )$的四个三角函数是反的。

1.2.2 表示任意的3D旋转与欧拉角

任意一个3D的旋转都可以表示成绕x轴、y轴、z轴旋转的组合，如下所示。

其中，$\alpha \beta \gamma$分别代表物体绕x、y、z旋转的角度，它们也被称为欧拉角。

把任意的旋转表示成矩阵：
Rodtigues旋转公式

2 MVP变换

2.1 定义

MVP变换是模型变换（M）、视图变换（V）、投影变换（P）的统称。MVP变换操作的是三维空间中的点，经过MVP变换后会被映射到标准二维平面上（实际上这个标准二维平面仍保留了z轴坐标）。

2.2 理解

想象一下拍照片的过程，拍照就是一个把三维转化为二维的操作：
（1） 找到一个风景优美的地方把人安排好。（这一步在图形学中叫做model transformmation 模型变换，相当于把模型和场景搭建好。
（2）确定相机的摆放，选好角度和位置来放相机（相当于view transformmation，视图变换）。
（3）拍照。（projection transformation 投影变换，把三维空间投影到二维图片。）

总结：
视图变换，是指变换照相机的位置，角度。
模型变换，是指变换被照物体的位置，角度。
投影变换，是指把三维空间投影到二维图片。

3 View / Camera Transformation 视图变换

视图变换，是指变换照相机的位置，角度。

3.1 确定相机摆放的三个因素

确定相机的摆放要确定以下三个因素：

• Position $\vec{e}$ —— 放在哪？
• Look-at / gace direction $\hat{g}$ —— 看谁？往哪看?
• Up direction $\hat{t}$ 相机的向上方向 —— 从哪个角度拍摄？
  

3.2 进行视图变换的方法

3.2.1 方便的表示相机

首先思考下面的问题：
首先如果一个相机和它拍摄的物品一起同样运动，那得到的投影会是相同的，如下所示。

所以有没有一个方便的方法来表示相机呢？

一个约定俗成的规矩就是我们把所有相机的：
（1）位置都固定在原点
（2）向上的方向都固定为Y轴正向
（3）看向的方向都是 -Z方向

（4）然后再让其他物体都与相机一起挪过来就好了。

3.2.2 移动相机的过程：

（1）把$\vec{e}$移向原点
（2）把$\hat{g}$的方向旋转到-Z
（3）把$\hat{t}$的方向旋转到Y
（4）把$(\hat{g}\times \hat{t})$旋转到X
我们把以上的过程写成矩阵形式：
$$M_{view}=R_{view}{T}_{view}$$
（1）首先求把$\vec{e}$移向原点的变换矩阵，如下所示，只是一个简单的平移变换矩阵：

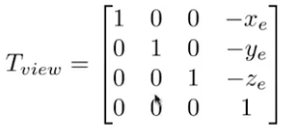
（2）然后求把$\hat{g}$的方向旋转到-Z，把$\hat{t}$的方向旋转到Y， 把$(\hat{g}\times \hat{t})$旋转到X的变换矩阵。

首先这个矩阵是个旋转矩阵，但是把以上三个方向旋转到坐标轴的旋转矩阵是非常难求的。

那么不妨动用一下逆向思维，求这个旋转矩阵的逆矩阵，即把X旋转到$g\times t$，Y旋转到t，Z旋转到-g，这个矩阵相对简单，如下所示。

$$R_{view}^{-1}=\left(\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right)$$

不理解的话可以用代表轴的列向量来验证一下，比如使用表示X轴列向量$(1,0,0,0{)}^T$来进行以下运算：
$$\left(\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right)\times \left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}{x}_{\hat{g}\times \hat{t}}\\ y_{\hat{g}\times \hat{t}}\\ z_{\hat{g}\times \hat{t}}\\ 0\end{array}\right)$$
Y轴和Z轴同理，都可以通过以上矩阵完成旋转。

然后，由于旋转矩阵是正交矩阵，矩阵的逆等于矩阵的转置，所以我们把它转置回来，就可以得到我们要的旋转矩阵：
$$R_{view}=\left(\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right)$$

4 Projection transformation 投影变换

投影是将3D转化为2D的变换。

4.1 正交投影和透视投影

投影变换包含两种：

• Orthographic projection 正交投影（没有近大远小）
• Perspective projection 透视投影（近大远小）
  

4.2 正交投影 Orthographic Projection

4.2.1 正交投影的简单的理解方式

• 相机处在原点，看向-Z，向上朝向Y
• 去掉空间中物体的Z坐标，得到一个矩形
• 把矩形的尺寸缩放到$[-1,1{]}^2$
  

4.2.2 普遍的理解方式

一、定义空间中的立方体，把立方体([l,r]$\times [b,t]\times [f,n]$)映射到正则(canonical)立方体$[-1,1{]}^3$ 上。

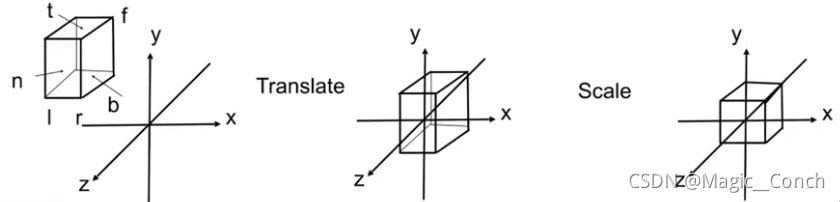
具体做法：

1. 把中心移到原点
2. 把x、y、z的值拉伸成[-1,1]

4.2.3 正交投影的变换矩阵

$$M_{ortho}=\left(\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right)$$
矩阵解读：（从右向左看）首先把中心点移到原点，然后缩放。

注意：n>f，近大于远。

4.3 透视投影

• 在图形学，艺术，虚拟系统中很常用。
• 近大远小。
• 投影后会使得平行的线不再平行。

在齐次坐标中，(1,0,0,1)和(2,0,0,2)表示的是同一个点。

4.3.1 如何做透视投影

• 首先把截头体(frustum)挤成立方体(cuboid)。(假设变换矩阵为：$M_{persp->ortho}$)
• 做正交投影(变换矩阵为：$M_{ortho}$)。
  

4.3.2 $M_{persp->ortho}$的推导

首先要寻找$(x^{{}^{\prime }},y^{{}^{\prime }},z^{{}^{\prime }})$和$(x,y,z)$的关系，先从侧面看，根据相似三角形得到以下关系。

同理，可得到x，y和x如下所示。

在齐次坐标系下，我们可以发现向量$(x,y,z{)}^T$发生了以下变化（z仍然未知），然后稍微转化一下形式，让列向量乘以n。

上面的式子说明，

所以，我们能够算出$M_{persp->ortho}$的一部分参数，如下所示。

然后，现在第三行还没有得出，我们观察一下与第三行相关的z，得到两个特点。

• 任何在近（n）面上的点没有变化。
  所以我们得到以下式子，(把z=n带进去，然后列向量乘以n)

可以看到结果列向量的第三行是$n^2$，所以第三行必须是(0,0,A,B)的形式。然后可以得到：

• 任何远（f）平面上点的z没有变化。
  这次我们选取原平面上的中心点(0,0,f,1)做为特殊点，得到：
  

最后解方程得到：

所以得到$M_{persp->ortho}$：
$$M_{persp->ortho}=\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right)$$

4.3.3 透视投影的变换矩阵$M_{persp}$

$$M_{persp}=M_{ortho}{M}_{persp->ortho}$$
$$M_{persp->ortho}=\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right)$$
$$M_{ortho}=\left(\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right)$$

5 视锥

5.1定义视锥的方法

从相机出发，看到一个近平面，并定义这个近平面的：

1. 长宽比(Aspect ratio)=宽度/高度（16:9）
2. 垂直可视角度(forV)（Field of View）：看到角度的范围。
   

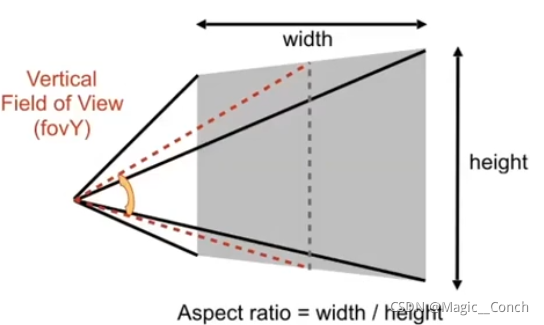
所谓广角就是可视角度比较大。

5.2 根据垂直可视角度和长宽比确定l,r,b,t（左，右，上，下）

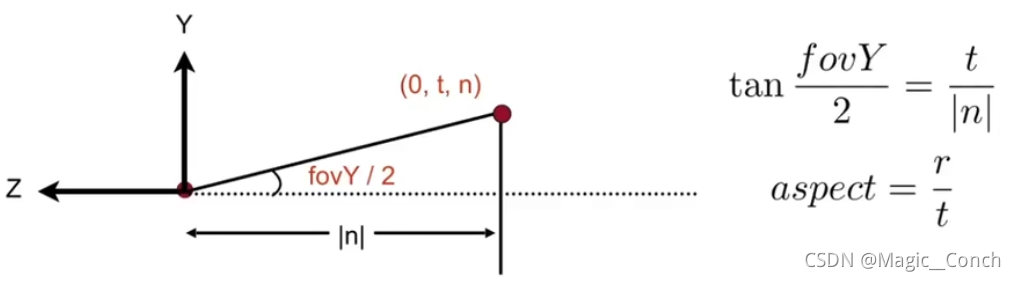
其中n是相机到近平面的距离。