整理得较为口语化,应该是比较好懂的啦~欢迎讨论问题,这篇配合“固定渲染管线”(我后续也会整理出来)的内容食用更佳哦!
目录
向量
【当我们需要用向量表示方向的时候,将其进行归一化(单位化)】
基础知识:
坐标系:

左手坐标系:左手半握手心朝上放在胸前:手臂指向为x轴,四指为y轴,拇指为z轴
右手坐标系:右手半握手心朝上在身侧平举,手臂指向为x,四指为y,拇指为z轴
向量有大小和方向,标量只有大小,没有方向。
*笛卡尔坐标系中,每一个向量都认为是以原点开始
特殊向量:
(1,0,0),(-1,0,0),(0,1,0),(0,-1,0),(0,0,1),(0,0,-1),(0,0,0)[零向量]
单位向量:模为1的向量
因点乘(dot)中cos只取正数,两个向量单位化后可以用来区分方向,零向量用来清零
向量相等:
数学意义上来说,是各分量相等,但是在游戏开发应用时一般是给定范围(如小数点后5位),小于某值则为相等
向量的计算:
向量求模与单位化:
向量求模:![]()
向量单位化:
零向量不能单位化,但可以进行求模
向量加法:
维数相同的两个向量才能进行向量加法,向量加法满足平行四边形或三角形法则。


向量的加法满足如下性质:
1)交换律:a+b=b+a; 2)结合律:(a+b)+c=a+(b+c);
3)a+0=0+a=a; 4)a+(-a)=(-a)+a=0。
向量减法:
向量减法可以看作是向量加法的逆运算。向量减法可按照三角形法则判断。

减法不满足交换律和结合律,交换后所得的结果模相等,方向相反
向量数乘:
标量与向量相乘称为向量的数乘。
向量数乘有以下性质:交换律和结合律
1)1• =
;
2)k•(l•)=(k•l) •
;
3)(k+l) • = k
+l
;
4)k(+
)= k
+k
;
向量点乘:
dot(·乘) :一般用于求夹角关系
[一般将向量单位化再进行,点乘用于求夹角,范围是0~180°]

通过点乘结果可判断两个向量的关系:cosθ
如果 = 0,那么向量相互垂直;
如果 > 0,那么向量 u 、v 之间的夹角小于90°;
如果 < 0,那么向量 u 、v 之间的夹角大于90°。
向量投影(只做了解):
给定两个向量v与n,可以把向量v分解为两个向量vx,vy,它们分别平行和垂直于向量n,把平行于向量n的向量vx称为向量v在向量n上的投影。

向量叉乘:
叉乘的结果是一个向量。u和v进行叉乘后得到另一个向量p,向量p同时垂直于 u 、v。[用于求法线],将x,y,z看作循环,xyzx……
向量的叉乘有如下性质:
1)反对称性:u×v=-v×u;
2)齐次性:(ku)×v=k(u×v);
3)可加性:u×(v+r)=u×v+u×r。
被乘数到乘数,是顺时针则物体是正面,逆时针则是背面,(背面裁剪的时候就可以将它裁剪掉,不用渲染)
光照模型
图形学中光的类型:点光源(没有方向),平行光(只有方向,没有位置),泛光灯(聚光灯)
(我的位置-点光源的位置=光线方向,平行光不需要求光线方向)
光照模型分类:光源(自发光),环境光,漫反射,镜面反射:反映物体表面光滑程度
(总光照 = 环境光 + 漫反射 + 镜面反射 + 自发光)
下面会介绍如何计算主要分量:
环境光(Ambient):
没有空间上的位置和方向的特征,只有一个颜色亮度值。
添加材质后:(反射能力和材质)
漫反射(Diffuse):
需要:光方向的逆方向和法线

光源的向量取反,将光线向量和法线单位化,然后进行点乘dot,再乘以物体的漫反射材质
添加材质后:
L应为光照射的反方向
镜面反射(Specular):
发生在光滑物体表面的高光反射中

需要:光线向量反方向、反射光向量,观察者方向(物体-我的位置)
[越和反射光向量重合,即α越小,看到的镜面反射光越强]
把观察者和光线向量的反方向单位化后相加得到夹角平分线,(即由向量求出的相应法线),单位化,再与单位化后的法线进行dot点乘,得到的角度越大,能看到的反射光越小。 最后进行pow加入极亮和泛光反应,pow的值越大表示极亮反应越强,越小表示泛光反应越强
添加材质后:
极亮反应,镜面反射集中在某一视角内,其他地方看不到
泛光反应:大部分范围都能看到
矩阵
(默认以(1,1)开头)m行n列的矩形表A称为一个m×n矩阵,记作
基础理论:
方阵:当m和n相等时,A称为一个n阶方阵。
单位矩阵:只有方阵(行列相等)才有单位矩阵,主对角线为1,其余都为0,乘任何矩阵都得到原矩阵,等价于数字1
零矩阵:可乘情况下,乘任何都为0,等价于数字0
单位矩阵和零矩阵没有逆矩阵
矩阵相等:如果两个矩阵具有相同的维数(同种矩阵)并且它们的元素都相等,则这两个矩阵相等。
矩阵计算:
矩阵加法:
只可以在两个同种矩阵之间进行。矩阵的和就是两个矩阵的对应元素相加的和组成的矩阵。
有如下性质:
1)交换律:A+B=B+A;
2)结合律:A+(B+C)=(A+B)+C;
3)存在与A同型的零矩阵0,使得0+A=A+0=A;
4)A+(-A)=0,-A称为A的负矩阵(每个成员取反)。
矩阵减法:
只能在两个相同维数的矩阵之间进行。即各分量相减
矩阵数乘:
矩阵与一个标量(或数量)相乘称为矩阵的数乘,即把数字乘到各分量里去
假设A,B是两个同型矩阵,k,l是两个标量,则有如下性质:
1)1•A=A,0•A=0;
2)(k+l)A = kA + lA;
3)k(lA)= l(kA)=(kl)A;
4)k(A+B)= kA+kB;
矩阵乘法:
矩阵A的列数需要和矩阵B的行数相等
A为m×n且B为n×p的矩阵,矩阵乘法结果为m×p的矩阵C,记作C=A×B。
在矩阵C中第ij个元素:A中第i个行向量和B中的第个j个列向量的点乘结果。
例:
假定有矩阵A、B、C满足矩阵乘法,则矩阵乘法有如下性质:
1)结合律:(AB)C=A(BC);
2)分配律:A(B+C)=AB+AC,(B+C)A=BA+CA;
3)存在单位阵与
,使得:
;
4)对于标量k,有k(AB)=A(kB)=(kA)B。
矩阵转置: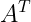
矩阵的转置指交换矩阵的行和列。
逆矩阵:
矩阵运算中没有除法运算,只有逆矩阵的运算。与原矩阵互为倒数,相乘得到单位矩阵(数字1),【单位矩阵和零矩阵没有逆矩阵】
1)只有方形的矩阵可以有逆矩阵。
2)一个n×n的矩阵M的逆矩阵表示为 。
3)将一个矩阵和它的逆矩阵相乘的结果是一个单位矩阵 。
4)并不是所有的方阵都有逆矩阵。
5)反序律:
6)还原性:
PS:向量中有一部分性质公式没有逐个修改成向量形式了(现在我只会笨方法,要一个一个修改比较慢),但都是看得懂的,欢迎指正!!!