一般套路
动态规划遵循一套固定的流程:递归的暴力解法->带备忘录的递归解法->非递归的动态规划解法
- 举个栗子: 斐波那契数列【力扣题目:509】
- 递归的暴力解法
function fib(n) {
if (n === 1 || n === 2) return 1;
return fib(n-1) + fib(n-2)
}

递归算法存在大量的重复计算,递归树体量巨大,耗费了大量的时间
–> 时间复杂度O(2^n)
==> 动态规划的第一个性质:重叠子问题
- 带备忘录的递归解法
递归的问题是存在大量的重复计算,故,解决问题~找一个备忘录给他记下来,备忘录可以选择数组也可以选择哈希表
var fib = function(n) {
var mem = [0, 1, 1];
if (n < 3) return mem[n];
var fn = function(n) {
var res = mem[n];
if (typeof res !== 'number') {
mem[n] = fn(n-1) + fn(n-2);
res = mem[n];
}
return res;
}
return fn(n);
};

–> 时间复杂度O(n)
- 非递归的动态规划解法
可以将“备忘录”独立作出一张表,完成自底向上的推算
var fib = function(N) {
let mem = [0, 1, 1];
if (n < 3) return mem[n];
for (let i=3; i<=n; i++) {
mem[n] = mem[n-1] + mem[n-2];
}
return mem[n]
}
引出 动态转移方程 这个名词
动态转移方程: 把f(n)想做一个状态n,这个状态n是由状态n-1和状态n-2相加转移而来,这就叫状态转移
做进一步优化将空间复杂度降为O(1)
var fib = function(N) {
if (N < 1) return 0;
if (N < 3) return 1;
let a = 0, b = 1, sum;
for (let i=0; i<N-1; i++) {
sum = a+b;
a = b;
b = sum;
}
return sum
};
当问题中要求求一个最优解或在代码中看到循环和max,min等函数时,十有八九需要动态规划
- 举个栗子:零钱兑换【力扣题目:322】
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
栗子:输入: coins = [1, 2, 5], amount = 11 输出: 3 解释: 11 = 5 + 5 + 1
- 递归的暴力解法
状态转移方程:
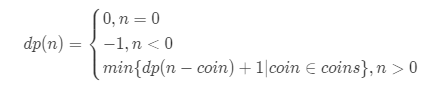
var coinChange = function(coins, amount) {
let db = function(n) {
if (n === 0) return 0;
if (n < 0) return -1;
let res = Infinity;
for (let i = 0; i < coins.length; i++) {
let subProblem = db(n - coins[i]) // 每次剩下的总额
if (subProblem === -1) {
continue;
}
res = Math.min(res, 1 + subProblem)
}
return res === Infinity ? -1 : res
}
return db(amount)
};
时间复杂度分析:子问题总数 x 每个子问题的时间。
结果: 超时
O(n^k) 总之是指数级别的。每个子问题中含有一个 for 循环,复杂度为 O(k)。所以总时间复杂度为 O(k * n^k),指数级别。
- 带备忘录的递归解法
var coinChange = function(coins, amount) {
let memo = {
};
let db = function(n) {
if (memo[n]) return memo[n]
if (n === 0) return 0;
if (n < 0) return -1;
let res = Infinity;
for (let i = 0; i < coins.length; i++) {
let subProblem = db(n - coins[i]) // 每次剩下的总额
if (subProblem === -1) {
continue;
}
res = Math.min(res, 1 + subProblem)
}
memo[n] = res === Infinity ? -1 : res
return memo[n]
}
return db(amount)
};
- 非递归的动态规划解法
var coinChange = function(coins, amount) {
let db = new Array(amount + 1).fill(Infinity);
db[0] = 0
for (let i = 1; i <= amount; i++) {
for (let coin of coins) {
if (i >= coin) {
db[i] = Math.min(db[i], db[i - coin] + 1)
}
}
}
return (db[amount] === Infinity) ? -1 : db[amount]
};
这个问题研究是看力扣题解中看懂的,具体内容不赘述,上链接:力扣题解
博弈问题
首先说说什么是博弈问题,这类问题的一般特点是:
- 模型为两人轮流决策的非合作博弈:两人轮流进行决策,并且两人都是用最优策略来获得胜利
- 博弈是有限的:无论两人怎样决策,都会在有限步后决出胜负
- 公平博弈:两人进行决策所遵循的规则相同
然后我们还是用一道题来看看吧:
- 石子游戏【力扣题目:1140】
亚历克斯和李继续他们的石子游戏。许多堆石子 排成一行,每堆都有正整数颗石子 piles[i]。游戏以谁手中的石子最多来决出胜负。
亚历克斯和李轮流进行,亚历克斯先开始。最初,M = 1。
在每个玩家的回合中,该玩家可以拿走剩下的 前 X 堆的所有石子,其中 1 <= X <= 2M。然后,令 M = max(M, X)。
游戏一直持续到所有石子都被拿走。
假设亚历克斯和李都发挥出最佳水平,返回亚历克斯可以得到的最大数量的石头。
示例:
输入:piles = [2,7,9,4,4] 输出:10 解释:
如果亚历克斯在开始时拿走一堆石子,李拿走两堆,接着亚历克斯也拿走两堆。在这种情况下,亚历克斯可以拿到 2 + 4 + 4 = 10 颗石子。
如果亚历克斯在开始时拿走两堆石子,那么李就可以拿走剩下全部三堆石子。在这种情况下,亚历克斯可以拿到 2 + 7 = 9 颗石子。
所以我们返回更大的 10。
- 定义dp数组的含义
- 状态转移方程
- 代码