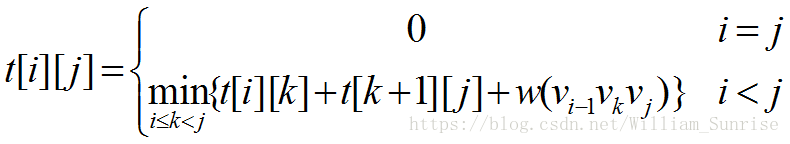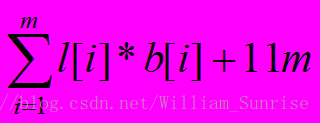动态规划
一、动态规划算法的思想
动态规划算法的基本思想是将待求解的问题问题分解成若干子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,分解得到的子问题往往不是相互独立的,计算时先保存已解决的子问题的答案,再自底向上计算出待求解的问题。
二、矩阵连乘问题
首先了解:①A是p x q矩阵,B是q x r矩阵,C=A x B是p x r矩阵,A x B需要pqr次乘法计算;②矩阵相乘满足结合律即 (AB)C=A(BC) ,多个矩阵相乘时不同的结合方式会有不同的乘法计算次数,通过不同的加括号方式找到最少的乘法计算次数即为要解决的问题。
#define MAX 100
int m[MAX][MAX] = {0}; //保存乘法计算次数的数组 ,可通过主函数输出
int s[MAX][MAX] = {0}; //保存断点(即加括号位置)的数组 ,可通过主函数输出
int p[MAX+1]; //保存矩阵行列值的数组 ,通过主函数数日
int n; //连续相乘的矩阵个数 ,通过主函数输入
void MatixChain(int m[][MAX],int s[][MAX],int p[],int n)
{
int i,j,r,k,t;
for(i=1;i<=n;i++) m[i][i] = 0;
for(r=2;r<=n;r++) //设置 j比i大 r-1
{
for(i=1;i<=n-r+1;i++)
{ //j-i=r-1 ,例如r=2时可计算m[1] [2],m[2][3]...,r=3时计算m[1][3],m[2][4],m[3][5],r=4时计算m[1][4],m[2][5]
j=i+r-1;
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j]; //首先计算断点为 i 时,矩阵连乘次数 ,用于下面的比较
s[i][j]=i; // 断点为 i
for(k=i+1;k<j;k++) //断点从 k=i+1 开始,直到断点为 k=j-1
{
t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]; //计算每一个断点下矩阵连乘次数
if(t<m[i][j]) //记录连乘次数少的次数及断点位置
{
m[i][j]=t;
s[i][j]=k;
}
}
}
}
}
三、最长公共子序列问题
例如序列X:A B C B D A B;序列Y:B D C A B A。则X和Y的最长公共子序列为:B D A B。
注意:最长公共子序列并不需要在原序列中是连续的。
#define MAX 100
char X[MAX]; //序列 X
char Y[MAX]; //序列 Y
int b[MAX][MAX]; //记录得到最长公共子序列的每一步的获得方式
int sx,sy; //X、Y 序列的长度
int C[MAX][MAX]={0}; //记录不同长度的 X和Y 序列,其最长公共子序列的长度
void LSCLength(char X[],char Y[],int b[][MAX],int sx,int sy,int C[][MAX])
{
int i,j,t;
for(i=1;i<=sx;i++) C[i][0]=0; //一个序列长度为0时,最长公共子序列长度为0
for(j=1;j<=sy;j++) C[0][j]=0; //同上
for(i=1;i<=sx;i++) //i,j 均从1 开始,体现了dp思想的先求解小问题并保存其解,自底向上原问题的解
{
for(j=1;j<=sy;j++)
{
if(X[i]==Y[j]) //序列的最后一个元素相同时 ,
{
C[i][j]=C[i-1][j-1]+1; //公共子序列长度至少为 1 ,且等于两序列去掉最后一个元素后的最长公共子序列长度 + 1
b[i][j]=1; //此方式下得到公共子序列为方式 1
}
else
{
if(C[i-1][j]>=C[i][j-1]) //两序列的最后一个元素不相等时,取 max(第一个序列去掉最后一个元素和第二个序列的LSCL,第二个序列去掉最后一个元素和第一个序列的LSCL)
{
C[i][j]=C[i-1][j];
b[i][j]=2; //第一个序列去掉最后一个元素和第二个序列的LSCL最大时为方式 2
}
else
{
C[i][j]=C[i][j-1]; //第二个序列去掉最后一个元素和第一个序列的LSCL最大时为方式 3
b[i][j]=3;
}
}
}
}
}
三、最大子段和
例如:序列:[-2,11,-4,13,-5,-2] 最大字段和为20,即[11,-4,13]相加。
注意:最大子段和所对应的序列是连续的。
#define MAX 1000
int b[MAX];
int s[MAX]; //输入的序列
int len; //输入序列的长度
int MaxSum(int b[],int s[],int len)
{
int i;
int sum=0;
b[0]=0; //每次计算都需初始化b[0]
for(i=1;i<=len;i++)
{
if(b[i-1]>0) //如果b[i-1]>0,则说明再往下加有可能得到更大的值,同样也有可能得到的值变小
//只需将执行每步 后所得的值与之前得到的sum相比较,变大则保存在sum中,变小则不保存
{
b[i]=b[i-1]+s[i]; //当前b[i-1]大于0,期望得到更大的值
}
else b[i]=s[i]; //不料b越加越小,已小于0,遇到一个值就保存一个,以期遇到大于0的值
if(b[i]>sum) sum=b[i]; //保存每步执行后的目前得到的最大值
}
return sum;
}
四、凸边形最优三角剖分
凸多边形:把一个多边形任意一边向两方无限延长成为一条直线,如果多边形的其他个遍均在此直线的同旁,那么这个多变形就是凸多边形。
凸多边形的三角剖分是一个将凸多边形分割成互不重叠的三角形的弦的集合T。
设t[i][j],1<=i<j<=n为凸子多边形{v[i-1],v[i],…,v[j]}的最优三角剖分所对应的权函数值,即最优值;s[i][j] 记录了v[i-1]和v[j]一起构成最优三角剖分的第三个顶点的位置。
w(v[i-1],v[k],v[j])为所构成的三角形的周长。
练习:给定七个顶点坐标分别为:(8,26)、(0,20)、(0,10)、(10,0)、(22,12)、(27,12)、(15,26),求此凸多边形的最优三角剖分权值,即最优分割点
部分解答如下:
五、图像压缩
计算机中常用像素点灰度值序列{P1,P2,…,Pn}表示图像。图像的变位压缩存储格式 是将灰度值序列分割成m个连续段S1,S2…,Sm,第i个像素段Si中,有l[i]个像素,(限制1<=l[i]<=255,所以每段需要用8位二进制数存储l[i]),l[i]个像素中,每个像素都用最大的像素所需要的二进数位数b[i]存储,(所以,1<=b[i]<=8,每段需要用3位二进制数存储b[i])。
按此格式存储像素序列,需要的存储空间(单位:比特)如下:
解题思路:
①考察最后一个元素P[i]的分段情况
②假设P[i]自成一段,则S[i]=S[i-1]+保存P[i]的代价
③假设最后两个像素点为一段,则S[i]=S[i-2]+保存P[i]的代价
④假设最后i个像素点为一段,则S[i]=S[0]+保存最后i个像素点的代价
⑤取S[i]为min时对应的元素个数,假设为k
⑥此时,则S[i]=S[i-k]+保存最后k个像素的代价
⑦保存最后k个像素的代价=k*max{k个灰度值二进制位数}+11
⑧求解S[i-k]