经典机器学习算法二：k近邻法

基于李航教授的《统计学习方法》，本博客为个人学习笔记。
只记录精华，不讲废话，让看过或没看过的你和我短时间重新领悟该方法。

k近邻法（knn）与k-means的比较：
两者共同点：
1、k的选择类似
2、思路：根据最近的样本来判断某个样本的属性
两者不同点：
1、应用场景：前者是分类或回归问题，后者是聚类问题
2、算法复杂度：前者是 $O(n^2)$，后者是 $O(kmn)$

一、模型

k近邻法是一种基本分类与回归方法。
它不属于判别模型，也不属于生成模型。

k近邻法实际上是对于输入的数据，在原训练集的空间上获得k个与其距离度量最相近的数据，由这k个数据的标签根据分类决策规则所决定该输入数据的输出标签。

因此模型由三个基本要素决定：距离度量、k值的选择、分类决策规则

1、距离度量

一般为Lp距离：
L1为曼哈顿距离
L2为欧式距离
L∞为切比雪夫距离

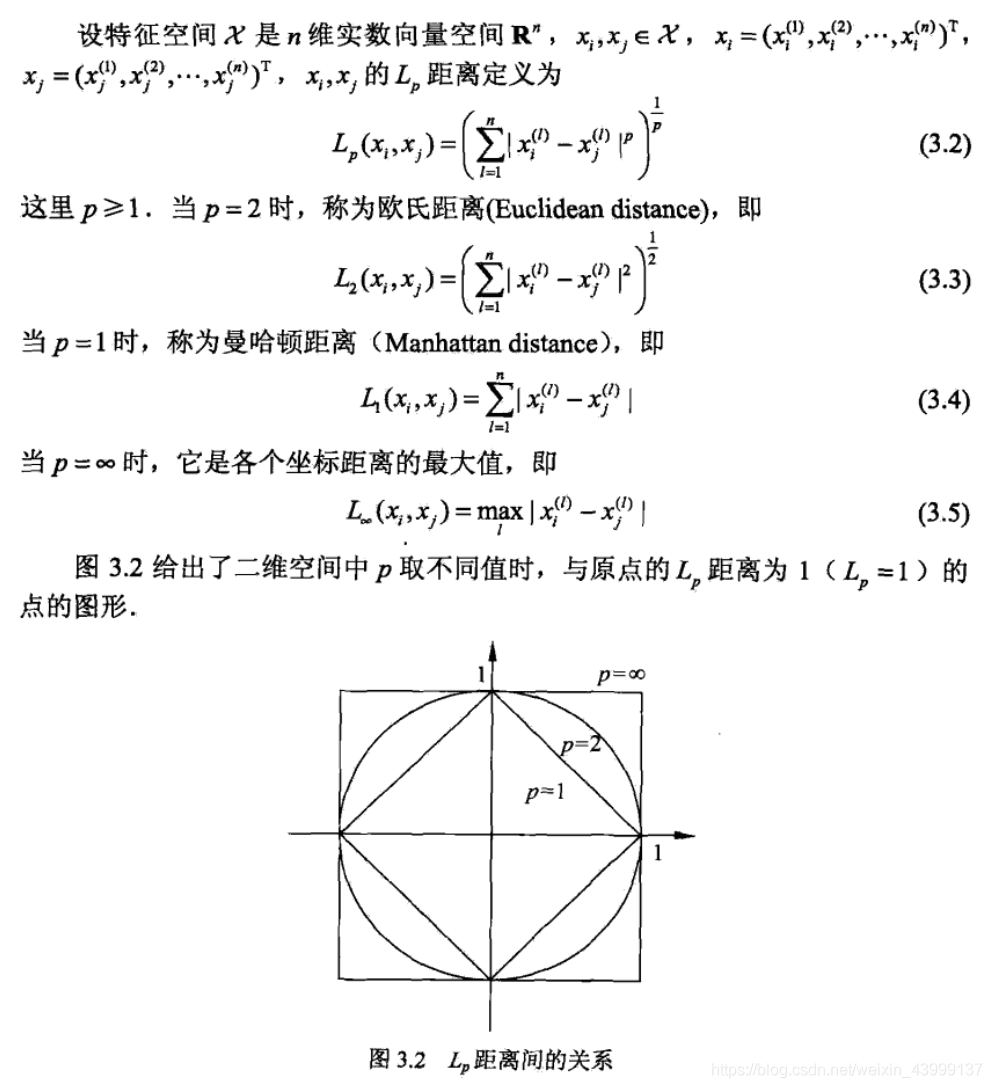
2、k值的选择

k值其实是一个超参数，得根据实际任务进行调整。
在应用中，k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。

3、分类决策规则

k近邻法中的分类决策规则往往是多数表决，即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类别。

二、策略

它不具备显式的学习过程，实际上是利用数据集对特征向量空间进行划分。
因此它的模型是固定的，不需要损失函数优化参数。

三、算法

1、线性扫描

线性扫描是实现knn最简单的方法。
简单来说，对于一个输入实例，我们首先要在训练集（假设n个数据）里找k个与其最接近的点，线性扫描，就要遍历一遍训练集，对于m个输入，算法复杂度即为 $O(m\times n)$。
所以训练集很大时，计算非常耗时，这种方法是不行的。

2、kd树

k-dimensional树的简称
为了提高k近邻搜索的效率，我们使用特殊的结构去存取训练数据，可以大大减少时间复杂度。
该特殊结构就是数据结构的最常见的二叉树，使用递归算法去构造该树。

构造kd树

我们对二叉树一个非常直观的感受就是：自上而下，不断分开。
其实kd树也就对应于一个K维空间，每一个维度的划分对应的是训练实例的其中一个特征的划分，维度空间K的大小取决于训练集的特征取值有多少。

（构造平衡kd树）算法实现：
输入：k维空间数据集 $T=\{x_1,x_2,…,x_N\}$，
其中 $x_i=(x_i^1,x_i^2,…,x_i^k)^T,i=1,2,...,N;$
输出：kd树。
（1）开始：构造根结点，根结点对应于包含T的k维空间的超矩形区域。 选择 $x^1$为坐标轴，以T中所有实例的 $x^1$坐标的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 $x^1$垂直的超平面实现。
由根结点生成深度为1的左、右子结点：左子结点对应坐标 $x^1$小于切分点的子区域，右子结点对应于坐标 $x^1$大于切分点的子区域。
将落在切分超平面上的实例点保存在根结点。

（2）重复：对深度为j的结点，选择 $x^l$为切分的坐标轴， $l=j(modk)+1$，以该结点的区域中所有实例的 $x^l$坐标的中位数为切分点，将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 $x^l$垂直的超平面实现。
由该结点生成深度为 $j+1$的左、右子结点：左子结点对应坐标 $x^l$小于切分点的子区域，右子结点对应坐标 $x^l$大于切分点的子区域。
将落在切分超平面上的实例点保存在该结点。

这里有两个细节：
1、我认为该重复步骤暗示了这里默认根结点的深度为0了。
2、选择的 $x^l$划分， $l$是取mod获得的，因此当 $j>=l$时，会重新使用前面已经使用过的特征对当前数据集进行划分，这样的划分不会形成新的维度，仍然是k维空间。

（3）直到两个子区域没有实例存在时停止。从而形成kd树的区域划分。

搜索kd树

（用kd树的最近邻搜索）算法实现：
输入：已构造的kd树；目标点x；
输出：x的最近邻。
（1）在kd树中找出包含目标点x的叶结点：从根结点出发，递归地向下访问kd树。若目 标点x当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点。直到子 结点为叶结点为止。
（2）以此叶结点为“当前最近点”。
（3）递归地向上回退，在每个结点进行以下操作：

• 如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最 近点”。
• 当前最近点一定存在于该结点一个子结点对应的区域。检查该子结点的父结点的 另一子结点对应的区域是否有更近的点。具体地，检查另一子结点对应的区域是否与以目标 点为球心、以目标点与“当前最近点”间的距离为半径的超球体相交。 如果相交，可能在另一个子结点对应的区域内存在距目标点更近的点，移动到另一个子 结点。接着，递归地进行最近邻搜索； 如果不相交，向上回退。

（4）当回退到根结点时，搜索结束。最后的“当前最近点”即为x的最近邻点。

总结该搜索算法：输入实例，自上而下直到叶结点，该叶结点所在的空间区域也是输入实例所分到的空间区域，但该区域内的结点不一定与输入实例最接近。因此又要自下而上的去判断是否有更接近的点。

如果实例点是随机分布的，kd树搜索的平均计算复杂度是 $O(logN)$，这里N是训练实例 数。kd树更适用于训练实例数远大于空间维数时的k近邻搜索。当空间维数接近训练实例数时，它的效率会迅速下降，几乎接近线性扫描。

在大量训练数据时，比较的次数大大减少，因为从空间上去看，它与最接近的点形成的一个球体，在超空间上是微不足道的，我们通过二叉树的存储，对空间的划分，能极大的优化我们找到最邻近点的时间。