机器学习最好的公开课——机器学习中的线性代数

本文为目前机器学习最好公开课——吴恩达机器学习的学习总结。

这篇文章我们来回顾机器学习中线性代数相关的知识。

矩阵和向量

矩阵和向量有关知识相信大家在线性代数中已经打好了基础，这里不再详细介绍，仅总结一些需要注意的地方防止出错。

• 矩阵的维数表示为行数×列数，例如 $R^{3×4}$ 表示一个 3 行 4 列的矩阵；
• 向量可以理解为只有 1 列的矩阵，向量的维数=向量中的元素个数；
• 关于下标索引从 1 开始还是从 0 开始，在今后的文章中，我们会默认从 1 开始，如有特例将会说明；

矩阵的加法和标量乘法

略，详细讲解见《线性代数》

矩阵向量乘法

矩阵与向量的乘法为矩阵与矩阵相乘的特例，直接略过，这里仅讲解一个小技巧。

假设我们有 4 个房屋的面积，房屋价格与房屋面积的公式如下图右边所示，我们可以通过构造矩阵与向量相乘的方式快速求解。

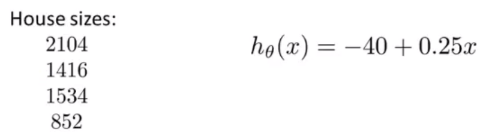
首先我们构造房屋大小的矩阵，其中第一列用来计算公式中的常数，第二列代表公式中的第二项 $x$。
$\left[ \begin{matrix} 1 & 2104\\ 1 & 1416 \\ 1 & 1534 \\ 1 & 852 \end{matrix} \right]$

再由公式构造向量：

$\left[ \begin{matrix} -40\\ 0.25 \\ \end{matrix} \right]$
矩阵和向量相乘得到的矩阵的每一行即为我们要求的解：
$\left[ \begin{matrix} 1 & 2104\\ 1 & 1416 \\ 1 & 1534 \\ 1 & 852 \end{matrix} \right]×\left[ \begin{matrix} -40\\ 0.25 \\ \end{matrix} \right]=\left[ \begin{matrix} -40+0.25×2104\\ -40+0.25×1416\\ -40+0.25×1534\\ -40+0.25×852\\ \end{matrix} \right]$
这样做有两个好处：

• 编程实现时代码更佳简洁。从原来的一个循环可以简化为只有一行代码（示例为 Octave）。并且如 Matlab 等软件是以矩阵为基础进行计算的。

  prediction = datamatrix * parameters
  

• 编程实现时，矩阵相乘的效率在数据量很大的时候远远高于循环求解。

矩阵与矩阵乘法

矩阵与矩阵的乘法可以在线性回归模型中计算参数 $\theta_0,\theta_1$，从而替代梯度下降算法。其实矩阵与矩阵的乘法也可以看作是矩阵与很多列向量相乘的结果，其过程可以参考《线性代数》。我们同样只讲解一个小技巧。

和前面矩阵与向量相乘的例子相同，但这次我们有 3 个假设函数，我们可以通过矩阵与矩阵相乘一次运算算出所有的解。

用左边的矩阵与右边矩阵的第一列向量相乘，得到等号右边矩阵的第一列，即第一个假设函数对应的 3 个预测值。我们用了一次运算，就计算出了 12 个结果，并且现在许多编程语言都提供了十分高效的线性代数库，它们都经过了高度优化，包括你计算机的 SIMD 并行，这些都可以很好地满足我们的一切需求。

矩阵乘法特征

这里我们只需要知道矩阵乘法满足结合律但不满足交换律，且单位矩阵的维度通常暗含的上下文中即可，不过多介绍。详细的讲解可参考《线性代数》。

逆和转置

矩阵的逆和转置的运算及定义不再详细介绍，具体可参考《线性代数》。但在机器学习中，对于矩阵的逆，我们需要做一些说明。

当今很多的编程语言都提供了矩阵的逆的求解，例如在 Octave 中可以用 pinv(A) 求解矩阵的逆，其中有圆整误差。

不是所有矩阵都有逆矩阵，例如元素都为 0 的方阵就没有逆矩阵，还有一些类似的矩阵也没有逆矩阵，可以将它们理解为接近 0 矩阵的矩阵。这种不存在逆矩阵的矩阵称为奇异矩阵或退化矩阵。

至此，我们简单的回顾了机器学习中矩阵相关的内容，如果你有线性代数的基础，那这些知识再简单不过了。接下来我们会运用这些工具构建更多的线性回归，并且推导一些强大的学习算法。