第二章 随机变量及其分布 2.2 离散型随机变量及其概率分布

2.2 离散型随机变量及其概率分布

一：离散型随机变量的分布律

特点：

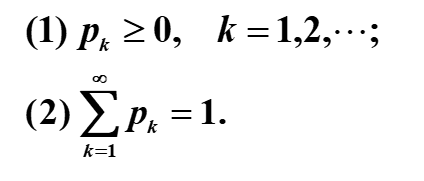
这个我们并不陌生，高中的时候那道概率题就是这种用求分布律的。我们画一个表格并要保证所有概率之和为1.

eg：

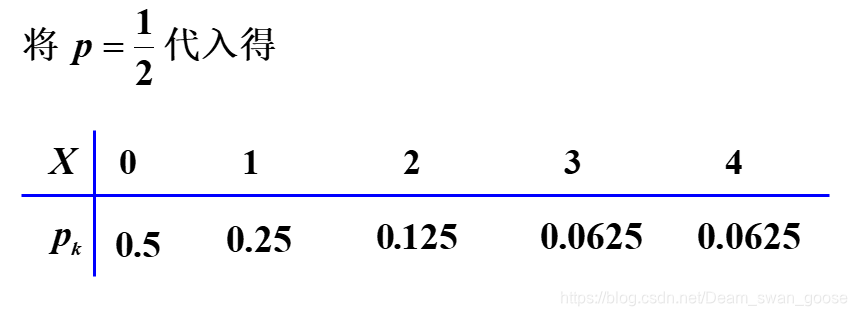
二：常见离散型随机变量的概率分布：

两点分布

两点分布是最简单的分布情况，他就两种情况，很好理解。

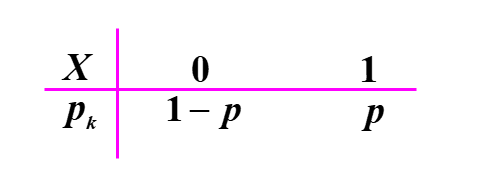
eg：

二项分布

这个高中的时候很常见，简单说就是：

<1>单次试验满足伯努利试验

<2>进行 $n$次伯努利试验后事件 $A$发生 $k$次的概率为：

例 1：

例 2：

泊松分布

这东西看着挺唬人，但是他其实是当 $n$趋近于无穷时二项分布的一个近似计算。二项分布如果平方数多的话会很不好算，所以我们引入这个。

• $np$ = $\lambda$
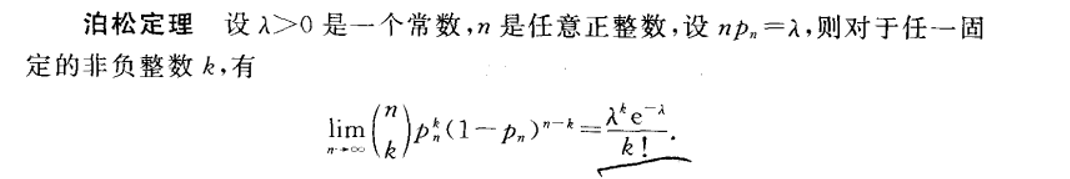
• 当 $n$ $\geq$ 20 , $p$ $\leq$ 0.05时可以用泊松分布近似代替二项分布。

eg：

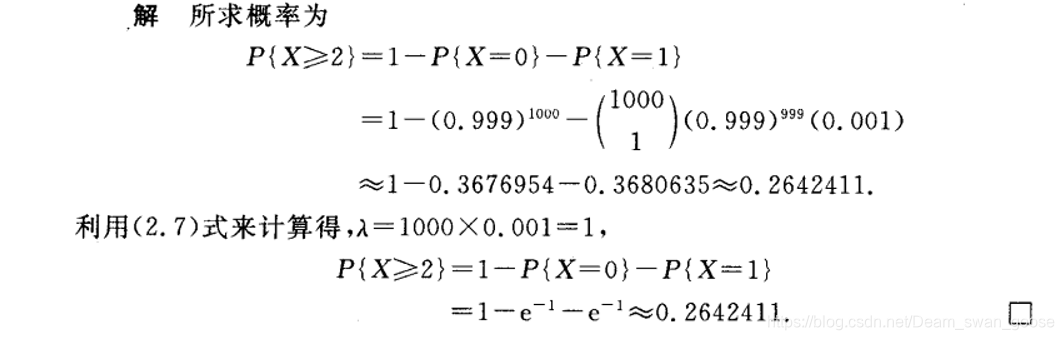
几何分布

观察可知，和二项分布相比这个不用去乘组合数。也就是符合几何分布模型每种情况的组合数都是1.

so：

超几何分布

适用于：
$N$ 个元素，其中 $N_1$为一类， $N_2$为第二类。不放回的取 $n$个元素。 $X:$取出的 $n$个元素中属于 $N_1$的个数。

$P$ { $X$ = $k$ } = $\frac{C_{N_1}^k C_{N_2}^{n-k}}{ C_N^n}$ , $k$ = 0,1,2,3……min( $n$, $N_1$)

例1:
一共有20名同学，其中男生15人，女生5人。现在任取4个人。 $X$:4人中女生的人数。

则 $P$ { $X$ = $k$ } = $\frac{C_5^k C_{15}^{4-k}}{ C_{20}^4}$ ， $k$ = 0,1,2,3

当总样本 $N$很大，抽取的 $n$很小时：我们可以把这个不放回抽样近似为放回抽样，这样我们就可以用二项分布来算了。如果二项分布不容易算出具体值可以再用泊松分布来代替。如下：

例2：
现在有10000粒种子，发芽率为99%，从中取200粒种子，求至多1粒不发芽的概率。

$X$ = 不发芽的种子数

$P$ { $X$ $\leq$ $1$ } = $P$ { $X$ = $0$ } + $P$ { $X$ = $1$ } = $\frac{C_{100}^0 C_{9900}^{200}}{ C_{10000}^{200}}$ + $\frac{C_{100}^1 C_{9900}^{199}}{ C_{10000}^{200}}$

这个显然不好算，因为 $\frac{n}{N}$ 比较小即使不放回也对剩下种子的发芽率影响很小，所以我们可以把这个近似成 $X$ ~ $b$(200,0.01)的二项分布。

此时 $P$ { $X$ $\leq$ $1$ } = $C_{200}^0$ $0.1^0$ $0.99^{200}$ + $C_{200}^1$ $0.1^1$ $0.99^{199}$

这样也不好算，但我们可以再把它转化为泊松分布 $X$ ~ $\pi$(2)

此时 $P$ { $X$ $\leq$ $1$ } = $\frac{2^0 e^{-2}}{0!}$ + $\frac{2^1 e^{-2}}{1!}$ = 0.1353 + 0.2707 = 0.406

总结一下：

可见，二项分布是对两点分布的推广，泊松分布是对二项分布的近似运算。