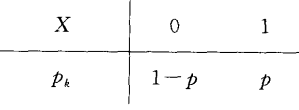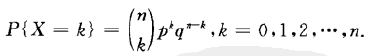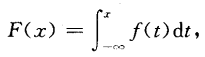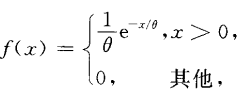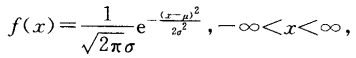本文用于复习概率论的相关知识点,因为好久不接触了,忘了不少。这里捡起来,方便学习其他知识。
总目录
本章目录
随机变量
用一个变量,来指代事件。
变量的值,来表示某个或某些事件。
例如:
事件
A_0:呼叫中心一个晚上接到0个电话。
A_1:呼叫中心一个晚上接到1个电话。
A_i:呼叫中心一个晚上接到i个电话。
...
那么,可以用一个随机变量X,来表示这些事件。
此处,X表示呼叫中心一个晚上接到电话的次数,那么:
这样,就可以用一个随机变量,来方便的表示某些事件的概率。
离散随机变量、分布律
X的取值,是离散的,比如1,2,3,...
随机变量X的所有取值x1,x2,...,有X的分布律表示为如下:
也可以用表格表示:
重要离散随机变量
(0-1)分布
分布律为:
表格表示为:
伯努利试验
只有0、1两种结果的试验,重复多次,每次之间没有影响。
二项分布
某种试验,发生的概率的p,不发生的概率是q
进行n次这种试验(每次相互独立,不相影响),发生了k次,分布律为:
发生k次,这种情况,一共有C(n,k)种。
每一种发生k次事件,的概率为p^k*q^{n-k}
把所有总数加起来,就得到上面的结果。
特别的,n=1时,二项分布就是一个(0-1)分布
泊松分布
以后再细说
泊松定理
分布函数
用一个函数,来表示随机变量X的分布律(离散)、或者一定范围的概率(连续)
例如:
上式称为随机变量X(大写X)的分布函数。
易知:
- 对于离散的随机变量X,P(x)的图像是一些离散的点,因为很多区间上的值为0
- 对于连续的随机变量X,P(x)的图像爱是啥是啥,看情况
所以:
- 对于离散的随机变量X,F(x)的图像是阶跃的
- 对于连续的随机变量X,F(x)的图像爱是啥是啥,看情况
分布函数性质:
连续随机变量、概率密度
对于一个连续随机变量X,它的概率分布函数由前面已经给出:
表示X在某些区间上的取值
概率密度函数
由于x是连续的,如果可以构造一个非负函数f(x),使其积分为F(X),如下:
那么,这个f(x),就称为随机变量X的概率密度函数。
重要连续型随机变量
这里只体现了概率密度,其概率分布函数、以及性质,自己看看就好,用到再说吧。
均匀分布
在一个区间内,概率密度是一个常数>0,这个常数跟区间有关, 其他是0。
记为:
X~U(a,b)
指数分布
概率密度是指数
正态分布
X服从参数为μ、σ的正态分布、或者高斯分布,记为:
X~N(μ,σ^2)
随机变量的函数的分布
要解决的问题:
已知,随机变量X的概率分布函数,为:
又知道,随机变量Y与X的关系为:
Y=g(X)
那么,求Y的分布律、或者概率分布函数、或者概率密度函数
这里涉及数学计算,具体情况具体分析吧。