快乐地打牢基础（8）——矩阵乘法

一、认识K阶常系数线性递推关系

---

形如 $F_n = a_1F_{n-1}+a_2F_{n-2}+...+a_kF_{n-k}$
其中： $a_1,a_2,...,a_k$是常数，有 $k$项，所以叫 $k$阶常系数线性递推关系。
写作： ${F_n = \displaystyle\sum^k_{i = 1}a_i\times F_{n-i}}$
我们常说的Fibonacci就是一个 $k$阶常系数线性递推关系。

二、矩阵的运算

---

1.矩阵的加减

对于都是 $n\times m$的矩阵 $A,B,C ，C = A+B$，则 $C_{ij} = A_{ij}\pm B_{ij}$。

2.矩阵乘法

设三个矩阵 $A,B,C$，且 $C= A*B$那么：

• Ⅰ. $A$的列数等于 $B$的行数。
• Ⅱ. $A$是 $n*r$的矩阵， $B$是 $r*m$的矩阵，则 $C$是一个 $n*m$的矩阵。
• Ⅲ. $C$的第 $i$行第 $j$列的元素 $C_{ij}$是矩阵 $A$的第 $i$行 和矩阵 $B$的第 $j$列的乘积之和。

3.矩阵的乘幂

$A$是一个方阵，将 $A$连乘 $n$次，即 $C = A^n$。
由于矩阵乘法满足结合律，因此我们可以用快速幂的思想来求方阵乘幂

三、矩阵乘法的应用

---

矩阵乘法的精深奥妙在于：

• Ⅰ.很容易将有用的状态存储在一个矩阵中。
• Ⅱ.通过状态矩阵与状态转移矩阵相乘可以快速得到一次DP的值（DP的状态转移方程必须是一次的递推式）。
• Ⅲ.求矩阵相乘的结果是要做很多次的乘法，这样的效率非常慢甚至不如原来的一次DP的转移，但是由于矩阵乘法满足结合律，可以先算后面的转移矩阵，即用快速幂，迅速地处理好后面的转移矩阵，再用初始矩阵乘上后面的转移矩阵得到的结果，算法的时间复杂度是 $O（logn）$级别。

【例题1】一本通OJ 1641 矩阵 $A\times B$
题意
矩阵 $A$ 规模为 $n×m$，矩阵 $B$ 规模为 $m×p$，现需要求 $A×B$。
思路
直接模拟矩阵乘法。

#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;

const ll N = 105;
ll n, m, p;

void MatrixMul(ll A[][N], ll B[][N], ll C[][N]){
    for(int i = 1; i <= n; i++){
        for(int j =1; j <= p; j++){
            for(int k = 1; k <= m; k++){
                C[i][j] += A[i][k] * B[k][j];
            }
        }
    }
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= p; j++){
            printf("%lld ",C[i][j]);
        }
        puts("");
    }

}
int main() {
    ll A[N][N], B[N][N], C[N][N] = {0};
    scanf("%lld %lld", &n, &m);
    //getchar();
    for(int i = 1 ; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%lld", &A[i][j]);
    scanf("%lld",&p);
    //getchar();
    for(int i = 1 ; i <= m; i++)
        for(int j = 1; j <= p; j++)
            scanf("%lld", &B[i][j]);
    MatrixMul(A, B, C);
    return 0;
}

【例题2】一本通OJ 1642 Fibonacci的第n项
题意
给出 $n$和 $m$，输出Fibonacci数列的第 $n$项模 $m$的结果。
$1\leq n \leq2 000,000,000$
$1\leq m \leq1 000,000,010$
思路
数据规模说明不可以直接递推，考虑矩阵乘法。
我们知道:
$f[i] = 1\times f[i-1]+1\times f[i-2]....................................(1)$
$f[i-1] = 1\times f[i-1]+0\times f[i-2]..............................(2)$
我们用矩阵乘法来表示这个式子。
$\left[ \begin{matrix} f[i]\\ f[i-1]\\ \end{matrix} \right]= \left[ \begin{matrix} 1&1\\ 1&0\\ \end{matrix} \right] \times \left[ \begin{matrix} f[i-1]\\ f[i-2]\\ \end{matrix} \right]= \left[ \begin{matrix} 1&1\\ 1&0\\ \end{matrix} \right] \times \left[ \begin{matrix} 1&1\\ 1&0\\ \end{matrix} \right] \times \left[ \begin{matrix} f[i-2]\\ f[i-3]\\ \end{matrix} \right].............(3)$
由 $(3)$可以进一步得到：
$\left[ \begin{matrix} f[n+1]\\ f[n]\\ \end{matrix} \right]= \left[ \begin{matrix} 1&1\\ 1&0\\ \end{matrix} \right]^{n-1} \times \left[ \begin{matrix} f[2]\\ f[1]\\ \end{matrix} \right]$
因为此题主要是要求 $f[n]$,所以再变一下下就是（也可以不变看个人习惯吧）：
$\left[ \begin{matrix} f[n]\\ f[n-1]\\ \end{matrix} \right]= \left[ \begin{matrix} 1&1\\ 1&0\\ \end{matrix} \right]^{n-2} \times \left[ \begin{matrix} f[2]\\ f[1]\\ \end{matrix} \right]$
$f[1]$和 $f[2]$是已知的，那么我们目前的主要面临的问题就是高效求出矩阵的 $n-2$ 次幂，朴素算法肯定是不够的，既然整数可以快速幂，那么我们矩阵也有快速幂。
其原理和普通的整数快速幂是一样的。也是将次幂用二进制分解，只不过是将整数乘变成了矩阵相乘。

#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;

const ll N = 3;
ll n, m, p;
//矩阵乘法
void MatrixMul(ll A[][N], ll B[][N], ll C[][N]) {
    ll res[N][N];
    memset(res, 0, sizeof(res));
    for(int i = 1; i < N; i++) {
        for(int j = 1; j < N; j++) {
            for(int k = 1; k < N; k++) {
                res[i][k] = (res[i][k] + (A[i][j] * B[j][k]) % m) % m;
            }
        }
    }
    memcpy(C, res, sizeof(res));
}

//矩阵快速幂
void Matrix_qpow(ll A[][N], ll b) {
    ll res[N][N], tmp[N][N];
    memset(res, 0, sizeof(res));
    memset(tmp, 0, sizeof(tmp));
    //构建一个单位矩阵
    for(ll i = 1; i < N; i++)
        res[i][i] = 1ll;
    for(int i = 1; i < N; i++){
        for(int j = 1;j < N; j++){
            tmp[i][j] = A[i][j];
        }
    }
    while(b) {
        if(b & 1) {
            MatrixMul(res, tmp, res);
        }
        MatrixMul(tmp, tmp, tmp);
        b >>= 1;
    }
    memcpy(A, res, sizeof(res));
}
ll solve(ll f[][N]) {
    ll res;
    //快速幂求 矩阵的n-2次幂
    Matrix_qpow(f, n - 2);
    res = f[1][1] * 1ll + f[2][1] * 1ll;
    res = res % m;
    return res;
}
int main() {
    ll f[N][N];
    scanf("%lld %lld", &n, &m);
    f[1][1] = 1;
    f[1][2] = 1;
    f[2][1] = 1;
    f[2][2] = 0;
    ll ans = solve(f);
    printf("%lld\n", ans);
    return 0;
}

【例题3】Fibonacci 前 n 项和
题意
求Fibonacci 前 n 项和。
思路
设前缀和数组为 $S[]$首先可以想到一个简单的递推式：

$S[n] = S[n-1]+f[n]..................................................................(4)$

由 $(1)$式可得

$S[n] = 1\times S[n-1]+1\times f[n-1] + 1\times f[n-2] \ \ .......................(5)$

同时可以根据第二题的 $(1)(2)$两式得出

$f[n] = 0\times S[n-1]+1\times f[n-1] + 1\times f[n-2] \ \ .......................(6)$

$f[n-1] = 0\times S[n-1]+1\times f[n-1] + 0\times f[n-2] \ \ .......................(7)$

这样结合 $(5)(6)(7)$得出一个和例2相似的结论。
$\left[ \begin{matrix} S[n]\\ f[n]\\ f[n-1]\\ \end{matrix} \right]= \left[ \begin{matrix} 1 &1 & 1\\ 0 &1 & 1\\ 0 &1 & 0\\ \end{matrix} \right]^{n-2} \times \left[ \begin{matrix} S[2]\\ f[2]\\ f[1]\\ \end{matrix} \right]$
这样和例2一样的使用矩阵快速幂求出矩阵的次幂，再乘上 $\left[ \begin{matrix} S[2]\\ f[2]\\ f[1]\\ \end{matrix} \right]$即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#define ll long long
using namespace std;

const ll N = 4;
ll n, m;

void MatrixMul(ll A[][N], ll B[][N], ll C[][N]) {
    ll res[N][N];
    memset(res,0,sizeof(res));
    for(int i = 1; i < N; i++) {
        for(int j = 1; j < N; j++) {
            for(int k = 1; k < N; k++) {
                res[i][k] = (res[i][k] + (A[i][j] * B[j][k]) % m ) % m;
            }
        }
    }
    memcpy(C, res, sizeof(res));
}

void Matrix_qpow(ll A[][N], ll b) {
    ll res[N][N], tmp[N][N];
    memset(res, 0, sizeof(res));
    memset(tmp, 0, sizeof(tmp));
    for(int i = 1; i < N; i++)
        res[i][i] = 1ll;
    for(int i = 1; i < N; i++)
        for(int j = 1; j < N; j++)
            tmp[i][j] = A[i][j];

    while(b) {
        if(b & 1) {
            MatrixMul(res, tmp, res);
        }
        MatrixMul(tmp, tmp, tmp);
        b >>= 1;
    }
    memcpy(A,res,sizeof(res));
}
ll solve(ll f[][N]) {
    ll res = 0;
    Matrix_qpow(f, n - 2);
    res = f[1][1] * 2 + f[1][2] * 1 + f[1][3] * 1;
    res %= m;
    return res;
}
int main() {
    ll f[N][N] = {{0, 0, 0, 0},
        {0, 1, 1, 1},
        {0, 0, 1, 1},
        {0, 0, 1, 0}
    };
    scanf("%lld %lld", &n, &m);
    printf("%lld\n", solve(f));
    return 0;
}

【例题4】1644 ：佳佳的 Fibonacci
题意

$T(n)=F(1)+2F(2)+3F(3)+...+nF(n)\bmod m$

现在佳佳告诉你了一个 $n$ 和 $m$，请求出 $T(n)$ 的值。
思路
这一题的递推式想是想不出来的，所以参考一下一本通书上的思路
$T(n)$本身没有什么递推性，所以需要来构造：
借用例3的前缀和函数 $S[]$

$n*S[n] =(n*F[1]+n*F[2]+n*F[3]+...+n*F[n])$

${n*S[n] - T[n]= ((n-1)*F[1]+(n-2)*F[2]+n*F[3]+...+(n-n)*F[n])}$
${\ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\displaystyle\sum^{n-1}_{i = 1}(n-i)F[i]}$.

令 $H[n] = n*S[n] - T[n]$，那么 $T[n] = n*S[n] - H[n]$。所以求出 $H[n] ,S[n]$即可。

我们很不容易发现 $H[n] = H[n-1] + S[n-1]$.
这就很有意思，接下来我们就可以在例3的基础上得到：
$H[n] = 1\times H[n-1]+1\times S[n-1]+0\times f[n-1] + 0\times f[n-2] ........................(8)$

$S[n] = 0\times H[n-1]+1\times S[n-1]+1\times f[n-1] + 1\times f[n-2] ........................(9)$

$f[n] = 0\times H[n-1]+0\times S[n-1]+1\times f[n-1] + 1\times f[n-2] ....................... .(10)$

$f[n-1] = 0\times H[n-1]+0\times S[n-1]+1\times f[n-1] + 0\times f[n-2] ......................(11)$
$\left[ \begin{matrix} H[n]\\ S[n]\\ F[n]\\ F[n-1]\\ \end{matrix} \right]= \left[ \begin{matrix} 1 & 1 & 0 & 0\\ 0 &1 &1 & 1\\ 0 &0 &1 & 1\\ 0 &0 &1 & 0\\ \end{matrix} \right]^{n-2} \times \left[ \begin{matrix} H[2]\\ S[2]\\ F[2]\\ F[1]\\ \end{matrix} \right]$

练习POJ 3070

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
#define ll long long

const int N = 3;
ll n, m = 1e4;

void MatrixMul(ll A[][N], ll B[][N], ll C[][N]) {
    ll res[N][N];
    memset(res, 0, sizeof(res));
    for(int i = 1; i < N; i++) {
        for(int j = 1; j < N; j++) {
            for(int k = 1; k < N; k++) {
                res[i][k] = (res[i][k] + A[i][j] * B[j][k] % m ) % m;
            }
        }
    }
    memcpy(C, res, sizeof(res));
}
void Matrix_qpow(ll A[][N], ll b) {
    ll res[N][N];
    memset(res, 0, sizeof(res));
    for(int i = 1; i < N; i++)
        res[i][i] = 1ll;
    while(b) {
        if(b & 1) {
            MatrixMul(res, A, res);
        }
        MatrixMul(A, A, A);
        b >>= 1;
    }
    memcpy(A, res, sizeof(res));
}
ll solve(ll f[][N]) {
    ll res;
    Matrix_qpow(f, n - 2);
    res = f[1][1] + f[1][2];
    return res % m;
}
int main() {
    ll f[N][N];
    while(scanf("%lld", &n) && n != -1) {
        f[1][1] = 1;
        f[1][2] = 1;
        f[2][1] = 1;
        f[2][2] = 0;
        if(n == 0)
            printf("0\n");
        else if(n == 1)
            printf("1\n");
        else
            printf("%lld\n", solve(f));
    }
    return 0;
}

使用矩阵乘法优化DP

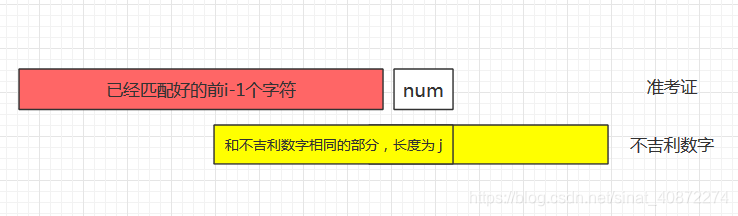
【例题 5 】BZOJ 1009 GT考试
题意
阿申准备报名参加GT考试，准考证号为N位数
$X1X2….Xn(0<=Xi<=9),$他不希望准考证号上出现不吉利的数字。
他的不吉利数学 $A1A2…Am(0<=Ai<=9)$有M位，不出现是指 $X1X2…Xn$中没有恰好一段等于 $A1A2…Am. A1$和 $X1$可以为0。

阿申想知道不出现不吉利数字的号码有多少种，输出模K取余的结果。
思路
采用DP的思路来做。

首先定义状态：
$f[i][j]$:准考证号前i位中 后j位与不吉利数的前j位相同时，前i位的方案数

那么 答案 $ans = f[n][0]+f[n][1]+…+f[n][m-1].$
状态转移：
$f[i][j]$可由 $f[i-1][k]$得到，其意义是在填完第i-1位之后，将其长为k的后缀后面再新添一位数num，之后这个i位数 与 不吉利数前缀相同的最长后缀是：后缀 j。

$i\geq 1时 \\f[i][j]=f[i-1][0]*a[0][j]+f[i-1][1]*a[1][j]+…+f[i-1][m-1]*a[m-1][j]。$

$i==0 时\\f[0][0]=1,f[0][other]=0$

其中， $a[k][j]$表示上面提到的num能取几个值，也就是有多少个 $f[i-1][k]$可以变成 $f[i][j]$， $k$是 $next[i],next$是KMP中的。

可以用KMP算法预处理出来，它是一个矩阵。

比如：还是假设不吉利数为123124，那么 $f[i][3]=f[i-1][2]+f[i-1][5]$，因为 $f[i-1][2]$末尾的???12不能是??12312，所以需要 $f[i-1][5]$补充
但若不吉利数为123123，那么 $f[i][3]=f[i-1][2]$，因为 $f[i][3]$末尾的???123不能是??123123
下面着重主要讲解这个矩阵的构造方式：
首先我们已经知道了：
$f[n][j]=f[n-1][0]*a[0][j]+f[n-1][1]*a[1][j]+…+f[n-1][m-1]*a[m-1][j]。$

那么我们可以得到这样一个式子：

$\left[ \begin{matrix} f[n][0]\\ f[n][1]\\ f[n][2]\\ ...\\ f[n][m-1]\\ \end{matrix} \right]= \left[ \begin{matrix} a_{00} & a_{01} & a_{02} & ...&a_{0,(m-1)}\\ a_{10} & a_{11} & a_{12} & ...&a_{1,(m-1)}\\ a_{20} & a_{21} & a_{22} & ...&a_{2,(m-1)}\\ ... & ... & ...& ...&...\\ a_{(m-1)0} & a_{(m-1)1} & a_{(m-1)2} & ...&a_{(m-1),(m-1)}\\ \end{matrix} \right] \times \left[ \begin{matrix} f[n-1][0]\\ f[n-1][1]\\ f[n-1][2]\\ ...\\ f[n-1][m-1]\\ \end{matrix} \right]$
我们将这个式子继续推广下去：
$\left[ \begin{matrix} f[n][0]\\ f[n][1]\\ f[n][2]\\ ...\\ f[n][m-1]\\ \end{matrix} \right]= \left[ \begin{matrix} a_{00} & a_{01} & a_{02} & ...&a_{0,(m-1)}\\ a_{10} & a_{11} & a_{12} & ...&a_{1,(m-1)}\\ a_{20} & a_{21} & a_{22} & ...&a_{2,(m-1)}\\ ... & ... & ...& ...&...\\ a_{(m-1)0} & a_{(m-1)1} & a_{(m-1)2} & ...&a_{(m-1),(m-1)}\\ \end{matrix} \right]^{n} \times \left[ \begin{matrix} f[0][0]\\ f[0][1]\\ f[0][2]\\ ...\\ f[0][m-1]\\ \end{matrix} \right]$

设 $a[][]$的n次方是 $A[][]$，原本
$f[n][0]=f[0][0]*A[0][1]+f[0][1]*A[0][1]+…+f[0][m-1]*A[0][m-1]。$
同时我们又知道：

$i==0 时，f[0][0]=1,f[0][other]=0$

所以

$f[n][0] = A[0][0]\\f[n][1] = A[1][0]\\f[n][2] = A[2][0]\\...\\f[n][m-1] = A[m-1][0]$;

$ans = f[n][0]+f[n][1]+…+f[n][m-1]\\\ \ \ \ \ \ \ \ =A[0][0] * f[0][0] + A[1][0]*f[0][0] + ...+A[m-1][0]*f[0][0]\\\ \ \ \ \ \ \ \ =A[0][0] + A[1][0] + ...+A[m-1][0]$

#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;

const ll N = 25;
int nex[N] = {0};
ll a[N][N] = {0};
ll n,m,k;
char s[N];
void get_next(){
    int j=0;
    for(int i=2;i<=m;i++)
    {
        while(j&&s[j+1]!=s[i])j=nex[j];
        if(s[j+1]==s[i])j++;
        nex[i]=j;
    }
}
void MatrixMul(ll A[][N],ll B[][N],ll C[][N]){
    ll res[N][N];
    memset(res,0,sizeof(res));
    for(int i = 0; i < m; i++){
        for(int j = 0; j < m; j++){
            for(int q = 0; q < m; q++){
                res[i][q] = (res[i][q] + A[i][j] * B[j][q] % k) % k;
            }
        }
    }
    memcpy(C,res,sizeof(res));
}
void Matrix_qpow(ll A[][N],ll b){
    ll res[N][N];
    memset(res,0,sizeof(res));
    for(int i = 0 ; i < m; i++)
        res[i][i] = 1ll;
    while(b){
        if(b & 1){
            MatrixMul(res,A,res);
        }
        MatrixMul(A,A,A);
        b >>= 1;
    }
    memcpy(A,res,sizeof(res));
}
void solve(){
    ll kk,res = 0;
    get_next();
    for(int i = 0 ; i < m; i++){
        for(int j = 0; j <= 9; j++){
            kk = i;
            while(kk && (s[kk + 1] - '0'!= j)) kk = nex[kk];
            if(s[kk + 1] - '0' == j) kk++;
            a[kk][i]++;
        }
    }
    Matrix_qpow(a,n);
    for(int i = 0; i < m; i++)
        res =(res + a[i][0]) % k;
    printf("%lld",res);
}
int main(){
    scanf("%lld %lld %lld",&n,&m,&k);
    scanf("%s",s + 1);
    solve();
    return 0;
}