背包问题:
有一个容量为 N 的背包,要用这个背包装下物品的价值最大,这些物品有两个属性:体积 w 和价值 v。
定义一个二维数组 dp 存储最大价值,其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。设第 i 件物品体积为 w,价值为 v,根据第 i 件物品是否添加到背包中,可以分两种情况讨论:
第 i 件物品没添加到背包,总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值,dp[i][j] = dp[i-1][j]。
第 i 件物品添加到背包中,dp[i][j] = dp[i-1][j-w] + v。
第 i 件物品可添加也可以不添加,取决于哪种情况下最大价值更大。因此,0-1 背包的状态转移方程为:
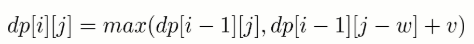
public int 01backPack(int W, int N, int[] weights, int[] values) {
int[][] dp = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
int w = weights[i - 1], v = values[i - 1];
for (int j = 1; j <= W; j++) {
if (j >= w) {
/* 如果第i件物品可装,那么装上第i件物品后的最大价值计算方式是,
先将状态转移到“不装第i件(i-1),但体积可装i的时候(j-w[i])”
用这个时候的最大价值+装i后的价值,即dp[i][j]=dp[i-1][j-w[i]]+v[i]*/
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w] + v);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[N][W];
}
空间优化
在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道,前 i 件物品的状态仅与前 i-1 件物品的状态有关,因此可以将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。此时,
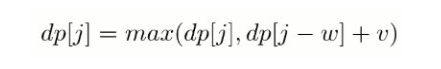
因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
public int optimize01backpack(int W, int N, int[] weights, int[] values) {
int[] dp = new int[W + 1];
for (int i = 1; i <= N; i++) {
int w = weights[i - 1], v = values[i - 1];
for (int j = W; j >= 1; j--) {
if (j >= w) {
dp[j] = Math.max(dp[j], dp[j - w] + v);
}
}
}
return dp[W];
}
1.划分数组为和相等的两部分
/*
* 题目:划分数组为和相等的两部分
* */
public boolean canPartition(int[] nums) {
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if (sum % 2 != 0) return false;
int half = sum / 2;
boolean dp[][] = new boolean[nums.length][half + 1];//dp[i][j]表示用前i个数字是否可以组成j
if (nums[0] <= half) dp[0][nums[0]] = true;
//初始化
for (int i = 1; i < nums.length; i++) {
for (int j = 0; j <= half; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= nums[i]) dp[i][j] = dp[i][j] || dp[i - 1][j - nums[i]];
}
}
return dp[nums.length - 1][half];
}
2.改变一组数的正负号使得它们的和为一给定数
/*
* 题目描述:给你一个非负整数的列表,a1 a2,…现在你有两个符号+和-。对于每个整数, 您应该从+和-中选择一个作为它的新符号。
* 找出有多少种分配符号的方法使整数的和等于目标S。
* sum(p):所有正数的和;sum(n):所有负数的和;sum所有数的和
* sum(p)+sum(n)=sum
* sum(p)-sum(n)=s
* sum(p)=(sum+s)/2
* 问题转化为了数组中某几个元素的和为sum(p)的方案有多少种
*
* */
public int findTargetSumWays(int[] nums, int S) {
int sum = 0;
int n = nums.length;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if (sum < S || (sum + S) % 2 == 1) return 0;
int sump = (sum + S) / 2;//找到 组成sump的组合有多少种
int dp[][] = new int[nums.length][sump + 1];//dp[i][j]表示使用前i个数字组成j的组合数
if (sump >= nums[0]) dp[0][nums[0]] = 1;
dp[0][0] = 1;
if (nums[0] == 0) dp[0][0] = 2;
for (int i = 1; i < n; i++) {
dp[i][0] = dp[i - 1][0];
if (0 >= nums[i]) {
dp[i][0] += dp[i - 1][0 - nums[i]];
}
}
for (int i = 1; i < n; i++) {
for (int j = 1; j <= sump; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= nums[i]) dp[i][j] += dp[i - 1][j - nums[i]];
}
}
return dp[n - 1][sump];
}
3.用m个0和n个1组成的字符串的最多的数量
/*
* 题目:用m个0和n个1组成的字符串的最多的数量
* 题目描述:数组中有很多个字符串,用有限的0,1数,组成的最多的字符串的数量
* 分析:这是一个多维费用的 0-1 背包问题,有两个背包大小,0 的数量和 1 的数量。
* */
public int findMaxForm(String[] strs, int m, int n) {
if (strs == null || strs.length == 0) return 0;
int dp[][] = new int[m + 1][n + 1];//dp[i][j]表示 用i个0,j个1组成的字符串的最多数量
for (int k = 0; k < strs.length; k++) {
int zeroCount = 0;
int oneCount = 0;
for (char c : strs[k].toCharArray()) {//计算当前串0,1的数量
if (c == '0') zeroCount++;
if (c == '1') oneCount++;
}
for (int i = m; i >= zeroCount; i--) {//dp[i][j]的更新基础是:i,j都大于当前串的0,1数量
for (int j = n; j >=oneCount; j--) {
//dp[i][j]等于 不加入该串(dp[i][j])跟加入该串(dp[i - zeroCount][j - oneCount] + 1)相比 哪个多
dp[i][j] = Math.max(dp[i][j], dp[i - zeroCount][j - oneCount] + 1);
}
}
}
return dp[m][n];
}
4.找零钱的最少硬币数(硬币可以重复使用)
/*
* 找零钱的最少硬币数(硬币可以重复使用)
* 题目描述:给一些面额的硬币,要求用这些硬币来组成给定面额的钱数,并且使得硬币数量最少。硬币可以重复使用。
* 物品:硬币
* 物品大小:面额
* 物品价值:数量
* 解析:因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包的逆序遍历 dp 数组改为正序遍历即可。
*
* */
public int coinChange(int[] coins, int amount) {
if (coins.length == 0 || amount == 0) return 0;//注意这个条件
int dp[] = new int[amount + 1];//初始化组成所有钱数的 最少硬币数为0
/*
//初始化
for(int i=0;i<coins.length;i++){
if(amount>=coins[i]) dp[coins[i]]=1;
}
*/
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j < amount + 1; j++) {
/*
* 遍历到硬币coins[i]时,当前零钱j的最少硬币数有三种情况(s.t j>=coins[i]):
* 1.为1 即当前硬币数和零钱数相等,只用当前硬币数量1就可以组成当前零钱数。(相当于做了一个初始化,提前初始化也可,如上面注释部分)
* 2.为dp[j-coins[i]]+1 此时当前零钱还没有组成方案(dp[j]==0),但使用当前硬币,结合之前的状态可组成 (dp[j-coins[i]]!=0)
* 3.为Math.min(dp[j], dp[j - coins[i]]+1) 此时当前零钱已经有了组成方案(dp[j]!=0);使用当前硬币,结合之前的状态也可组成 (dp[j-coins[i]]!=0)。则两者作比较,取少的
* 4.除上述情况外,dp[j]不更新。(为0 用目前的硬币没有办法组成该零钱数(dp[j]==0&&dp[j-coins[i]]==0);不为0,已经有了组成方案(dp[j]!=0),但若再使用当前硬币不可组(dp[j-coins[i]]==0)。所以无需更新
* */
if (j - coins[i] == 0) {
dp[j] = 1;
}else if (dp[j - coins[i]] != 0 && dp[j] != 0) {
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
} else if (dp[j - coins[i]] != 0 && dp[j] == 0) {
dp[j] = dp[j - coins[i]] + 1;
}
}
}
if (dp[amount] == 0) return -1;
return dp[amount];
}
5.题目:找零钱的硬币数组合(硬币可以重复用)
/*
* 题目:找零钱的硬币数组合(硬币可以重复用)
* */
public int change(int amount, int[] coins) {
if(amount==0||coins.length==0) return 0;
int dp[]=new int[amount+1];
dp[0]=1;
for (int i=0;i<coins.length;i++){
for(int j=coins[i];j<=amount;j++){
dp[j]+=dp[j-coins[i]];
}
}
return dp[amount];
}
/*
*
* 分析完全背包和01背包的区别。
* dp[i][j]代表,用截止到第i个物品时,背包容量为j时的最大价值。
* 完全背包:物品可以重复用.dp[i][j] = max(dp[i][j], dp[i][j - ci] + wi )。编码技巧:空间压缩后,内层循环用正序。
* 01背包:物品不可重复用,dp[i][j] = max(dp[i][j], dp[i-1][j - ci] + wi)。编码技巧:空间压缩后,内层循环用倒序(为了避免覆盖 截止到用上一个物品时的dp[j-obj[i]]值,即dp[i-1][j-obj[i]])
*
* 使用空间压缩方法:dp[j]代表背包容量为j时的最大价值,空间压缩后,两种背包dp[j]的更新公式为:dp[j]=max(dp[j],dp[j-ci]+wi)。
* 但不同的是:
* 完全背包 :对背包容量j的遍历用正序:因为dp[j]的更新值不光受dp[i-1][j-ci]的影响,还受dp[i][j-ci]的影响.
* dp[j]=max(dp[j],dp[j-ci]+wi),正向遍历时,dp[j-ci]含义是dp[i][j-ci]
* 01背包:对背包容量j的遍历用倒序:因为dp[j]的更新只受dp[i-1][j-ci]的影响,ci不可以重复用,跟dp[i][j-ci]无关,dp[i-1][j-ci]不可以被dp[i][j-ci]覆盖。所以为了避免覆盖截止到用上一个物品时的价值dp[i-1][j-obj[i]],而影响到dp[j]的更新,所以用反向遍历。
* dp[j]=max(dp[j],dp[j-ci]+wi),反向遍历时,dp[j-ci]含义是dp[i-1][j-ci]
* */
6.字符串按单词列表分割
求解有顺序的完全背包问题时,对物品的迭代应该放在最里层,对背包的迭代放在外层,只有这样才能让物品按一定顺序放入背包中。
/*
* 字符串按单词列表分割
* 分析:有顺序的完全背包问题
* */
public boolean wordBreak(String s, List<String> wordDict) {
boolean dp[]=new boolean[s.length()+1];//dp[j]表示遍历到第j个字符时是否可以实现合成
/*
下面这种做法,没有考虑的word的顺序,会出现这样的问题:比如这样一个wordDict={"apple","an","He","has"},s="He has an apple"
dp[j]只能记录遍历到第j字符时用前[i]个word是否可以合成。比如此时遍历到word:‘an’、字符:‘n’,此时满足条件word.equals(s.substring(j-len,j)。
但dp[j]=dp[j]||dp[j-len]=false(即dp['n']=dp['n']||dp['s'],dp['s']=false,含义是用前两个word不能合成"Hehas")。当word遍历到"has",字符遍历到's'时,实现了dp['s']=true。
但,却已无法影响但"has"后面的字符"an"和"apple"。这两个word已经被迭代过去了。无法实现匹配。因此dp['n']和dp['e']不能满足更新条件,只能停留在false阶段
word顺序的问题导致不能成功合成。
for(String word:wordDict){
int len=word.length();
for(int j=word.length();j<s.length();j++){
if(word.equals(s.substring(j-len,j)))
dp[j]=dp[j]||dp[j-len];
}
}
*/
/*
* 解决方案:求解有顺序的完全背包问题时,对物品的迭代应该放在最里层,对背包的迭代放在外层,只有这样才能让物品按一定顺序放入背包中。
* */
dp[0]=true;
for(int j=1;j<=s.length();j++){
for(String word:wordDict){
int len=word.length();
if(j>=len&&word.equals(s.substring(j-len,j)))
dp[j]=dp[j]||dp[j-len];
}
}
return dp[s.length()];
}
7.组合总和(不同的顺序代表不同的组合)
/*
* 题目:组合总和(不同的顺序代表不同的组合)
*
* 背包在外层循环
* */
public int combinationSum4(int[] nums, int target) {
int dp[]=new int[target+1];
dp[0]=1;
for(int j=1;j<=target;j++){
for(int i=0;i<nums.length;i++){
if(j>=nums[i]) dp[j]+=dp[j-nums[i]];
}
}
return dp[target];
}
