1.正定矩阵,半正定矩阵以及负定矩阵
矩阵所有特征值都大于零,则是正定矩阵
矩阵所有的特征值都不小于零,则是半正定矩阵
矩阵所有的特征值都小于零,则是负定矩阵
2.凸函数定义,海塞矩阵半正定性数学和几何意义
凸函数:任意属于定义域的两个自变量x1和x2,且对于任意0 =< a <= 1,如果函数f()满足f(a*x1+(1-a)) =< a*f(x1)+(1-a)f(x2),那么函数f()是凸函数。形象上的理解如下图所示,函数曲线上任意两点的连线一定在函数曲线的上方:

多元函数的海塞矩阵半正定性就相当于一元函数二阶导非负性,因此凸函数的海塞矩阵一定是半正定。要想真正的理解凸函数海塞矩阵半正定性,需要从泰勒展开说起,
下式是一元函数泰勒二阶展开:
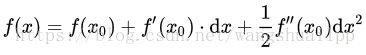
如果函数f(x)是凸函数,那么必定当一阶导为零时,二阶导必须大于等于零,这样才满足f(x)存在极小值。
下式是多元函数泰勒展开,此时二阶导数变成了海塞矩阵:
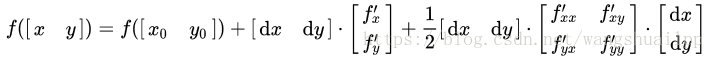
如果一阶导为0,是不是极小值完全取决于不同的dx, dy下,能不能做到最后一项一直非负。只有对于任意dx和dy,[dx,dy]H[dx,dy]T一直非负的情况,我们才能说这是极小值。如果一直非正,这就是极大值。如果它一会正一会负,就是鞍点。因此凸函数海塞矩阵是半正定矩阵。
3.高斯牛顿下降法中增量矩阵H半正定性
高斯牛顿法的实质也是用泰勒展开得到的,二次型来代替原函数,利用二次型的极值点的情况,逼近原函数的极值点。按照上面凸函数的推导,这里其实也是求一个极小值点,说白了也是一个凸函数的极值点。这里的增量矩阵就是凸函数的海塞矩阵。因此要满足高斯牛顿法有极小值点,必须要求增量矩阵半正定性。这里引用高翔视觉SLAM十四讲中内容,当增量矩阵为半正定型时,可能会出现奇异矩阵和病态的情况,此时增量的稳定性较差,因此高斯牛顿法要求增量矩阵为正定性,但实际情况下是半正定。