Resumen de tipos de preguntas de matemáticas avanzadas
- 1. Funciones, Límites y Continuidad
-
- (1) Determinación de la acotación, monotonicidad, periodicidad e impar-par de funciones
- (2) función compuesta
- (3) El concepto y la naturaleza del límite
- (4) Límites izquierdo y derecho
- (5) Encuentra el límite
- (6) Juicio de continuidad y propiedades de funciones continuas.
- (7) Tipos de discontinuidades
1. Funciones, Límites y Continuidad
(1) Determinación de la acotación, monotonicidad, periodicidad e impar-par de funciones
1. Monotonicidad
2. Paridad
Funciones impares comunes : sinx, tanx, arcsinx, arctanx, ln 1 − x 1 + x, ln (x + 1 + x 2), ex − 1 ex + 1, f (x) − f (−x) sinx, tanx , arcsinx, arctanx, ln\frac{1-x}{1+x}, ln(x+\sqrt{1+x^2}),\frac{e^x-1}{e^x+1} , f(x)-f(-x)s i n x ,t a n x ,a r c s i n x ,a r c t a n x ,l n1 + x1 - x,l norte ( x+1+X2) ,mix +1mix -1,f ( x )−f ( -x ) _
Funciones pares comunes : x 2 , ∣ x ∣ , cosx , f ( x ) + f ( − x ) x^2, |x|, cosx, f(x)+f(-x)X2,∣x∣,c o s x ,f ( x )+f ( -x ) _
3. Periodicidad
! Si f ( |} es el períodoSi f ( x ) tiene período T , entonces f ( a x _+segundo ) con∣ un ∣tpara el periodo
4. Limitación
∣ sinx ∣ ≤ 1 , ∣ cosx ∣ ≤ 1 , ∣ arcsinx ∣ ≤ π 2 , ∣ arccosx ∣ ≤ π |sinx| \leq1,|cosx| \leq1,|arcsinx| \leq\frac{\pi}{2},|arccosx| \leq\pi∣ sen x ∣ _ _≤1 ,∣ c o s x ∣≤1 ,∣ a r c s yo n x ∣≤2pag,∣ a r c c o s x ∣≤Pi
Suplemento: funciones comunes
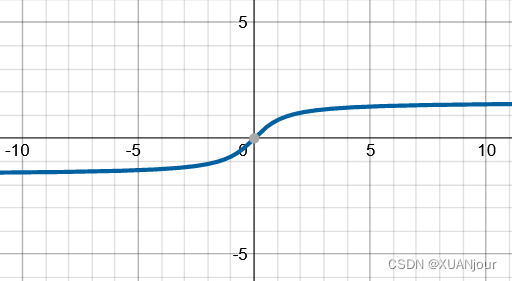
1) y = arctan x y=\arctan x y=arctánx
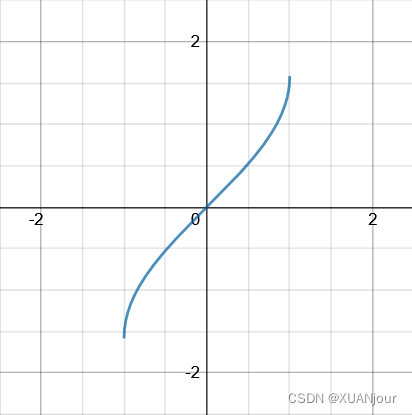
2)y = arcosen xy=\arcsin xy=arcosinx
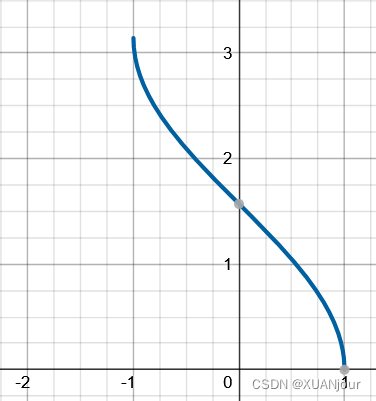
3) y = arccos x y=\arccos x y=arccosx
4) Función de signo:
y = sgnx= { − 1 , x < 0 0 , x = 0 1 , x > 0 \begin{cases} -1, x<0\\ 0, x=0\\ 1, x >0\\ \end{casos}⎩⎪⎨⎪⎧− 1 ,x<00 , x=01 x _>0
5) Función de redondeo: y = [ x ] y = [x]y=[ x ]
x − 1 < [ x ] ≤ x x-1<[x]\leq xX−1<[ x ]≤X
(2) función compuesta
La capitalización sólo es posible cuando la intersección del dominio de la función externa y el dominio de valor de la función interna no está vacía.
(3) El concepto y la naturaleza del límite
1. El concepto de límites
1) límite de secuencia
∀ ϵ > 0 , ∃ N > 0 , cuando n > N , siempre hay ∣ xn − a ∣ < ϵ , entonces se llama lim x → ∞ xn = a \forall \epsilon>0, \exists N>0 , cuando Cuando n>N, siempre hay |x_n-a|< \epsilon, entonces se llama\displaystyle\lim_{x\to\infty}x_n=a∀ ϵ>0 ,∃ norte>0 , cuando n>Cuando N , siempre hay ∣ xnorte−un ∣<ϵ , entonces se llamax → ∞límXnorte=a
!b < a , ∃ N , 当 n > N 时 , xn > b b<a,\exists N,当n>N时,x_n >bb<a , ∃ N , este n>Cuando norte , xnorte>b
!c > a , ∃ N , 当 n > N 时 , xn < c c>a,\exists N,当n>N时,x_n <cC>a , ∃ N , este n>Cuando norte , xnorte<c
! El límite del límite de secuencia {x} no tiene nada que ver con el término finito anterior.¡ El límite del límite de secuencia { x } no tiene nada que ver con el término finito anterior
! Límite general∃ ⇒ Límite parcial∃ Límite general\exists\RightarrowLímite parcial\existsLímite global ∃⇒Límite parcial∃
! _ Todos los límites parciales ∃ ⇒ Límites totales ∃ Todos los límites parciales \exists\Rightarrowwhole limits\existsTodos los límites parciales ∃⇒Límite global ∃
2) Límite de función
(1) Cuando la variable independiente tiende a infinito:
lim x → + ∞ \lim_{x\to+\infty}Limx → + ∞
∀ ϵ > 0 , ∃ X > 0 , cuando x > \exists∀ ϵ>0 ,∃ X>0 , cuando x>Cuando X , siempre hay∣ f ( x ) _−Un ∣<ϵ , entonces se llamax → + ∞límf ( x )=a
lim x → − ∞ \lim_{x\to-\infty}Limx → − ∞
∀ ϵ > 0 , ∃ X > 0 , cuando x < − , \exists∀ ϵ>0 ,∃ X>0 , cuando x<Cuando − X , siempre hay ∣ f ( x )−Un ∣<ϵ , entonces se llamax → − ∞límf ( x )=a
lim x → ∞ \lim_{x\to\infty}Limx → ∞
∀ ϵ > 0, ∃ X > 0, cuando ∣ x ∣ > , \exists∀ ϵ>0 ,∃ X>0 , cuando ∣ x ∣>Cuando X , siempre hay∣ f ( x ) _−Un ∣<ϵ , entonces se llamax → ∞límf ( x )=a
(2) La variable independiente tiende a un valor finito:
∀ ϵ > 0 , ∃ δ > 0 , cuando 0 < ∣ x − x 0 ∣ > δ , siempre existe ∣ f ( x ) − A ∣ < ϵ , entonces se llama lim x → ∞ f ( x ) = A \ forall \epsilon>0, \exists \delta>0, cuando 0<|x-x_0|>\delta, siempre hay |f(x)-A|< \epsilon, entonces se llama \displaystyle\lim_ {x\a \infty}f(x)=A∀ ϵ>0 ,∃δ _>0 , cuando 0<∣x _−X0∣>Cuando δ , siempre hay ∣ f ( x )−Un ∣<ϵ , entonces se llamax → ∞límf ( x )=A
! x → xo , pero x ≠ xo [es decir, lim x → ∞ f ( x ) no tiene nada que ver con si f ( x ) existe] infty}f(x) no tiene nada que ver con si f(x) existe】X→Xo,pero xq=Xo【es decirx → ∞límf ( x ) no tiene nada que ver con si f ( x ) existe ]
2. Naturaleza de los límites
1) Propiedades generales
(1) Limitación
Convergencia → \a→ Hay un límite, pero no al revés
(2) Protección de números
(3) Relación con lo infinitesimal
lim f ( x ) = A ↔ f ( x ) = A + α ( x ) , [donde lim α ( x ) = 0 ] \lim f(x) = A\leftrightarrow f(x) = A + \ alfa(x), [donde\lim\alpha(x) = 0]Limf ( x )=A↔f ( x )=A+α ( x ) , [ dondeLimun ( x )=0 】
2) Criterios de existencia
(1) Criterio de sujeción
(2) Criterio acotado monótono
3. Algoritmo extremo
(1) Reglas de operación racional
limf (x) = A, limg (x) = B limf(x) = A,limg(x) = Bl i m f ( x )=A , l i m g ( x )=B , entonces
- lim ( f ( x ) ± g ( x ) ) = limf ( x ) ± g ( x ) lim(f(x)\pm g(x)) = limf(x) \pm g(x)l i m ( f ( x )±gramo ( x ) )=l i m f ( x )±g ( x )
- lim ( f ( x ) × g ( x ) ) = f ( x ) × g ( x ) lim(f(x)\times g(x)) = f(x)\times g(x)l i m ( f ( x )×gramo ( x ) )=f ( x )×g ( x )
- limf ( x ) g ( x ) = limf ( x ) limg ( x ) , ( B ≠ 0 ) lim\frac{f(x)}{g(x)} = \frac{limf(x)}{limg( x)},(B \neq 0)yo soy _g ( x )f ( x )=l i m g ( x )l i m f ( x ),( B=0 )
(2) Atención
- existe ± \pm± no existe= == no existe
- No existe ±\pm± no existe= == no necesariamente
- existe × ÷ \times\div× ÷ no existe= == no necesariamente
- No existe × ÷ \times\div× ÷ no existe= == no necesariamente
(3) Conclusiones comunes
-
limf ( x ) = A ≠ 0 → limf ( x ) g ( x ) = A limg ( x ) limf(x) = A \neq 0 \rightarrow limf(x)g(x) = Alimg(x)l i m f ( x )=A=0→l i m f ( x ) g ( x )=A l i m g ( x )
significa:el límite del factor distinto de cero se puede encontrar primero -
limf ( x ) g ( x ) lim\frac{f(x)}{g(x)}yo soy _g ( x )f ( x )Existencia, limg ( x ) = 0 → limf ( x ) = 0 limg(x) = 0 \rightarrow limf(x) = 0l i m g ( x )=0→l i m f ( x )=0
-
limf ( x ) g ( x ) = A lim\frac{f(x)}{g(x)} = Ayo soy _g ( x )f ( x )=A,limf ( x ) = 0 → limg ( x ) = 0 limf(x) = 0 \rightarrow limg (x) = 0l i m f ( x )=0→l i m g ( x )=0
4. Pequeño sin taza
1) Orden infinitesimal: orden superior, orden k, mismo orden, equivalente
2) Propiedades infinitesimales
- La suma/producto de un número finito de infinitesimales sigue siendo infinitesimal
- El producto de una cantidad infinitesimal y una cantidad acotada sigue siendo infinitesimal
5. Mugendai
1) Comparaciones comunes de infinito:
A x → + ∞ \to+\infty→+ ∞时,ln α x ≪ x β ≪ ax ln^\alpha x \ll x^\beta\ll a^xl norteαx _≪Xb≪aX
Tonelada → ∞ \to\infty→∞时,ln α n ≪ n β ≪ an ≪ n ! ≪ nn ln^\alpha n\ll n^\beta \ll a^n\ll n! \lln^nl norteα sustantivo≪norteb≪anorte≪norte !≪nortenorte
2) Propiedades del infinito:
- El producto de dos infinitos sigue siendo infinito.
- La suma de infinito y variables acotadas sigue siendo una cantidad infinita
3) La relación entre infinito y variables ilimitadas:
- cantidad infinita → \a→ Variable ilimitada, pero no al revés [( − 1 ) n (-1)^n( -1 ) _norte】
4) La relación entre infinito e infinitesimal:
- f(x) f(x)f ( x ) es infinitesimal yf ( x ) ≠ 0 f(x)\neq 0f ( x )=0 , entonces1 f ( x ) \frac{1}{f(x)}f ( x )1es ∞ \infty∞
! Sif ( x ) ≠ 0 f(x)\neq 0f ( x )=0 , entonces1 f ( x ) \frac{1}{f(x)}f ( x )1sin sentido
(4) Límites izquierdo y derecho
- El límite de la función por partes en el punto de división.
- mi ∞ mi^\inftymi∞ límite de tipo
- arctan ∞ arctan\inftya r c t a n ∞ tipo límite
(5) Encuentra el límite
1. Encuentra el límite de la suma\producto de n términos
1) Encuentre primero la fórmula de la suma, luego encuentre el límite
2) Teorema de pellizco: la suma de n elementos falla y el grado del numerador y el denominador no es igual
3) Definición integral definida: el grado del numerador y el denominador son ambos iguales y el denominador es uno más que el grado del numerador.
2. Encontrar límites indefinidamente
(1) 0 0 \frac{0}{0}00
0 0 \frac{0}{0}00: { Equivalente a la ley de L'Hôpital infinitesimal: 0 0 o ∞ ∞ Fórmula de Taylor\begin{cases} Equivalente a la ley de L'Hôpital infinitesimal: \frac{0}{0} o \frac{\infty}{\infty }\\ Fórmula de Taylor\\ \end{casos}⎩⎪⎨⎪⎧Equivalente a infinitesimalLey de Lópida : _00o∞∞fórmula de taylor
Suplemento: Equivalente a infinitesimal
- sinx , tanx , arcsinx , arctanx , ln ( 1 + x ) , ex − 1 ∼ x sinx,tanx,arcsinx,arctanx,ln(1+x),e^x-1 \sim xs i n x ,t a n x ,a r c s i n x ,a r c t a n x ,l n ( 1+x ) ,miX−1∼X
- hacha − 1 x ∼ lna \frac{a^x-1}{x}\sim lnaXax -1∼ln a _
- ( 1 + x ) α − 1 ∼ α x (1+x)^\alpha-1\sim \alpha x( 1+x )a−1∼αx _
- ( 1 + α ( x ) β ( x ) ) − 1 ∼ α ( x ) β ( x ) ( α ( x ) → 0 , α ( x ) β ( x ) → 0 ) (1+\alpha(x) ^{\beta(x)} )-1\sim \alpha (x)\beta(x) (\alpha(x)\rightarrow0,\alpha(x)\beta(x)\rightarrow0)( 1+un ( x )b ( x ) )−1∼un ( x ) b ( x ) (un ( x )→0 ,α ( x ) β ( x )→0 )
- 1 − cosx ∼ 1 2 x 2 1-cosx \sim \frac{1}{2}x^21−cos x _ _∼21X2
- x − ln ( 1 + x ) ∼ 1 2 x 2 x-ln(1+x)\sim \frac{1}{2}x^2X−l norte ( 1+x )∼21X2
- x − senx ∼ 1 6 x 3 x-senx\sim \frac{1}{6}x^3X−pecado _ _ _∼61X3
- arcsinx − x ∼ 1 6 x 3 arcsinx-x\sim \frac{1}{6}x^3arco s i n x _ _−X∼61X3
- tanx − x ∼ 1 3 x 3 tanx-x\sim \frac{1}{3}x^3tan x _ _−X∼31X3
- x − arctanx ∼ 1 3 x 3 x-arctanx\sim \frac{1}{3}x^3X−a r c t a n x∼31X3
Suplemento: Fórmula de reemplazo
- u ( x ) v ( x ) → ev ( x ) lnu ( x ) u(x)^{v(x)}\to e^{v(x)lnu(x)}tu ( x )v ( x )→miv ( x ) l norte u ( x )
- ln ( … … ) → ln ( 1 + △ ) ∼ △ ln(……)\to ln(1+\triangle)\sim \trianglel norte ( …… )→l norte ( 1+△ )∼△
- ( … … ) − 1 → { e △ − 1 ∼ △ ( 1 + △ ) a − 1 ∼ a △ (……)-1\to \begin{cases} e^\triangle-1\sim\triangle\\ (1+\triangle)^a-1\sim a\triangle \end{casos}( …… )−1→{ mi△−1∼△( 1+△ )a−1∼un △
(2)∞ ∞ \frac{\infty}{\infty}∞∞
∞ ∞ \frac{\infty}{\infty}∞∞: { 0 0 Ley de Lópida: 0 0 o ∞ ∞ lim x → + ∞ amxm + … … + a 1 x + a 0 bnxn + … … + b 1 x + b 0 = { 0 , m < n ∞ , m > nambn , m = n \begin{cases} \frac{0}{0}\\ Regla de Lópida: \frac{0}{0} o \frac{\infty}{\infty}\\ \ displaystyle\lim_{ x\to+\infty}\frac{a_mx^m+…+a_1x+a_0}{b_nx^n+…+b_1x+b_0}=\begin{casos} 0, m<n\\ \infty, m>n\\ \ frac{a_m}{b_n},m=n\\ \end{casos} \end{casos}⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧00Ley de Lópida : _00o∞∞x → + ∞límbnorteXnorte+……+b1X+b0amXmetro+……+a1X+a0=⎩⎪⎨⎪⎧0 , metro<norte∞ ,metro>nortebnorteam,metro=norte
Suplemento: infinito
-
A x → + ∞ \to+\infty→+ ∞时,ln α x ≪ x β ≪ ax ln^\alpha x \ll x^\beta\ll a^xl norteαx _≪Xb≪aX
-
Tonelada → ∞ \to\infty→∞时,ln α n ≪ n β ≪ an ≪ n ! ≪ nn ln^\alpha n\ll n^\beta \ll a^n\ll n! \lln^nl norteα sustantivo≪norteb≪anorte≪norte !≪nortenorte
-
cantidad infinita → \a→ Variable ilimitada, pero no al revés [( − 1 ) n (-1)^n( -1 ) _norte】
(3) 1 ∞ 1^{\infty}1∞
1 ∞ 1^{\infty}1∞ : Deformación de la identidad,(1 + △) 1 △ ∼ e (1+\triangle)^{\frac{1}{\triangle}}\sim e( 1+△ )△1∼mi
(4) ∞ 0 \infty^0∞0、0 ∞ 0^\infty0∞
{ ∞ 0 0 ∞ → u ( x ) v ( x ) → ev ( x ) lnu ( x ) \begin{cases} \infty^0\\ 0^\infty\\ \end{cases}\to u(x )^{v(x)}\to e^{v(x)lnu(x)}{ ∞00∞→tu ( x )v ( x )→miv ( x ) l norte u ( x )
(5) 0 × ∞ 0\veces\infty0×∞
0 × ∞ 0\times\infty0×∞:{ 0 1 ∞ → 0 0 ∞ 1 0 → ∞ ∞ \begin{cases} \frac{0}{\frac{1}{\infty}}\to\frac{0}{0}\\ \\ \frac{\infty}{\frac{1}{0}}\to\frac{\infty}{\infty}\\ \end{casos}⎩⎪⎪⎨⎪⎪⎧∞10→0001∞→∞∞
(6)∞ − ∞ \infty-\infty∞−∞
∞ − ∞ : → 0 × ∞ \infty-\infty:\to 0\times\infty∞−∞ :→0×∞ Igual que arriba
Suplemento: Principio de sustitución
- Este valor es un punto continuo en el intervalo de la función [ lim x → x 0 f ( x ) = f ( x 0 ) \displaystyle\lim_{x\to x_0}f(x) = f(x_0)x → x0límf ( x )=f ( x0)】
- Límite de factor parcial ∃ \exists∃即可拆分【∃ lim x → x 0 f ( x ) = A , lim x → x 0 [ f ( x ) ± g ( x ) ] = A + lim x → x 0 g ( x ) \exists\displaystyle\lim_{x\to x_0}f(x) = A,\displaystyle\lim_{x\to x_0}[f(x)\pm g(x)] = A + \displaystyle\lim_{x \a x_0}g(x)∃x → x0límf ( x )=Un ,x → x0lím[ f ( x )±g ( x ) ]=A+x → x0límg ( x ) (en preguntas que involucran números desconocidos, el límite debe eliminarse primero∃ \exists∃)
- Las relaciones de suma y resta se pueden intercambiar bajo ciertas condiciones
[ α ∼ α 1 , β ∼ β 1 , y { lim = α 1 β 1 = A ≠ 1 , entonces α − β ∼ α 1 − β 1 lim = α 1 β 1 = A ≠ − 1 , entonces α + β ∼ α 1 + β 1 \alpha \sim \alpha_1, \beta \sim \beta_1, y \begin{cases}\lim = \frac{\alpha_1}{\ beta_1} = A \neq 1 , luego \alpha - \beta \sim \alpha_1 - \beta_1\\ \lim = \frac{\alpha_1}{\beta_1} = A \neq -1 , luego \alpha + \beta \ sim \ alpha_1 + \beta_1\\ \end{casos}a∼a1, segundo∼b1, y{ Lim=b1a1=A=1 ,Entonces α−b∼a1−b1Lim=b1a1=A=− 1 ,Entonces α+b∼a1+b1】
3. Teorema del valor medio
(6) Juicio de continuidad y propiedades de funciones continuas.
1. Determinar la continuidad
1) Definición
设y = f ( x ) y=f(x)y=f ( x ) en el puntox 0 x_0X0Hay una definición en una determinada vecindad descentrada, entonces { lim △ x → 0 △ y = lim △ x → 0 [ f ( x 0 + △ x ) − f ( x 0 ) ] lim △ x → 0 f ( x ) = f ( x 0 ) \begin{casos} \displaystyle\lim_{\triangle x\to 0}\triangle y = \displaystyle\lim_{\triangle x\to 0}[f(x_0+\triangle x) -f (x_0)]\\ \displaystyle\lim_{\triangle x\to 0}f(x) = f(x_0)\\ \end{cases}⎩⎨⎧△ x → 0lím△ y=△ x → 0lím[ f ( x0+△ x )−f ( x0) ]△ x → 0límf ( x )=f ( x0)
2) teorema
① f ( x ) y g ( x ) f (x) y g (x)f ( x ) y g ( x ) están en el puntox 0 x_0X0son continuas, entonces f ( x ) ± g ( x ) , f ( x ) g ( x ) , f ( x ) g ( x ) ( g ( x ) ≠ 0 ) f (x)\pm g(x), f(x)g(x),\frac{f(x)}{g(x)}(g(x)\neq 0)f ( x )±g ( x ) ,f ( x ) g ( x ) ,g ( x )f ( x )( g ( x )=0 ) es continua en el punto
②Supongamos que la función u = ϕ ( x ) u = \phi (x)tu=ϕ ( x ) en el puntox 0 x_0X0es continua en , y ϕ ( x 0 ) = u 0 \phi (x_0) = u_0ϕ ( x0)=tu0, función y = f ( u ) y = f(u)y=f ( u ) puntou 0 u_0tu0es continua en , entonces y = f [ ϕ ( x ) ] y = f[\phi(x)]y=f [ ϕ ( x ) ] enx = x 0 x = x_0X=X0Continuo en todas partes
③Las funciones elementales básicas son continuas dentro de su dominio.
④Las funciones elementales son continuas dentro de su intervalo de definición
2. Propiedades de funciones continuas
设f ( x ) ∈ C [ a , b ] f(x)\in C[a,b]f ( x )∈C [ a ,segundo ]
1)(m,M)f ( x ) f(x)f ( x ) tiene min en [a,b], MAX
2)(acotado) ∃ k > 0, de modo que ∣ f ( k∃ k>0 , de modo que ∣ f ( x ) ∣≤k
3)(punto cero) y f ( a ) f ( b ) < 0 , ∃ c ∈ [ a , b ] , de modo que f ( c ) = 0 y f(a)f(b)<0, \exists c\ en [a,b], haga f(c)=0Y f ( a ) f ( b )<0 ,∃c _∈[ un ,b ] , de modo que f ( c )=0
4)(valor intermedio) ∀ η ∈ [ m , M ] , entonces ∃ ξ ∈ [ a , b ] , de modo que f ( ξ ) = η \forall\eta\in[m,M], entonces \exists\ xi \in[a,b], de modo que f(\xi)=\eta∀ η∈[ metro ,M ] , entonces ∃ ξ∈[ un ,b ] , de modo que f ( ξ )=el
(7) Tipos de discontinuidades
Categoría 1: f ( a − 0 ) = f ( a + 0 ) f(a-0)=f(a+0)f ( un−0 )=f ( un+0 ) todos tienen valores
{Puede eliminar puntos discontinuos: f ( a − 0 ) = f ( a + 0 ) ≠ f ( a ) Saltar puntos discontinuos: f ( a − 0 ) ≠ f ( a + 0 ) \begin{cases} Puede eliminar puntos discontinuos : f(a-0)=f(a+0)\neq f(a)\\ Punto de discontinuidad de salto: f(a-0)\neq f(a+0)\\ \end{cases}{ Puede eliminar discontinuidades : f ( a _−0 )=f ( un+0 )=f ( a )Punto de discontinuidad de salto : f ( a−0 )=f ( un+0 )
La segunda categoría: f ( a − 0 ) , f ( a + 0 ) f(a-0), f(a+0)f ( un−0 ) 、f ( un+0 ) Al menos uno no existe
Antes de juzgar el punto de discontinuidad (es decir, antes de encontrar el límite), defórmelo si puede y no se apresure a sustituirlo.