信号与系统(Python) 学习笔记 (7) 电路与系统函数

• 【总目录】
  • (1) 简介 Intro
  • (2) 傅里叶 Fourier
    • 常用函数的傅里叶变换汇总
  • (3) LTI 系统 与 滤波器
    • 二次抑制载波振幅调制接收系统 Python
  • (4) 取样 Sampling
  • (5) 离散傅里叶 Discrete Fourier
  • (6) 拉普拉斯变换 Laplace Transform
  • (7) 电路与系统函数
    

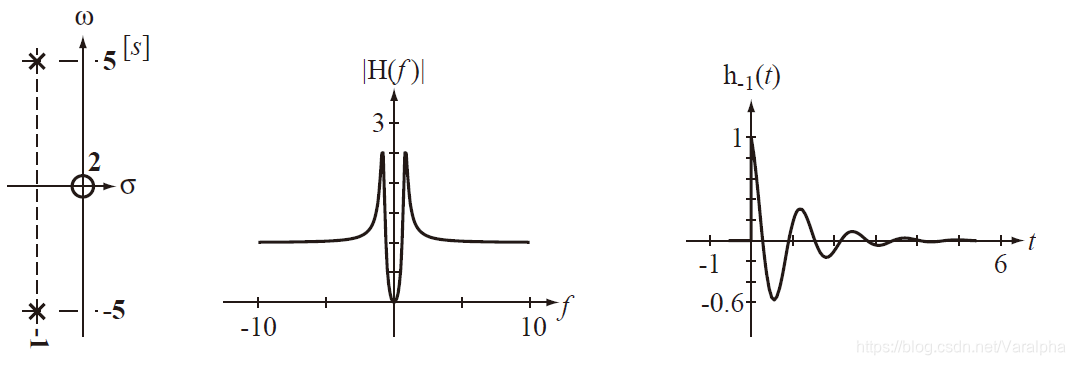
7. 电路与系统函数

---

7.1. 电路分析

• 电路求解 有两部分因素：

  1. 内部约束 – 元件的伏安关系 VAR
  2. 外部约束
     1. 节点 – KCL $\sum I_K = 0$
     2. 回路 – 能量守恒 电压降代数和为零 KVL $\sum U_k = 0$

• 知道 电路结构和参数，依据两种约束，求直流电流、电压。

7.1.1. 电路的s域模型

电路元件的s域模型

• 对时域电路取拉氏变换：

  1. 电阻:
     $u(t) = R\cdot i(t) \to U(s) = R\cdot I(s)$
     

  2. 电感:
     $\begin{aligned}\displaystyle u(t) = L\frac{di_L(t)}{dt} &\to \displaystyle U(s) = sL\cdot I_L(s)-L\cdot i_L(0_-) \\ i_L(t) = i_L(0_-)+\frac{1}{L} \int^{t}_{0_-}u_L(\tau)d\tau &\to I_L(s) =\displaystyle \frac{1}{sL}U_L(s)+\frac{i_L(0_-)}{s} \end{aligned}$
     

     • 电流源并联阻抗和电压源串联阻抗的相互转换：
       1. 阻抗数值不变
       2. 源的数值满足欧姆定律的关系 电压 $=$电流 $\times$阻抗
       3. 产生的电流方向一致

  3. 电容:
     $\begin{aligned}\displaystyle i(t) = C\frac{du_C(t)}{dt} &\to \displaystyle I(s) = C\cdot U_C(s) - C\cdot u_C(0_-) \\ u_C(t) = u_C(0_-)+\frac{1}{C} \int^{t}_{0_-} i_C(\tau)d\tau &\to U_C(s) =\displaystyle \frac{1}{sC}I(s)+\frac{u_C(0_-)}{s} \end{aligned}$
     

     • 电流源并联阻抗和电压源串联阻抗的相互转换：
       1. 阻抗数值不变
       2. 源的数值满足欧姆定律的关系 电压 $=$电流 $\times$阻抗
       3. 产生的电流方向一致

  4. 电源
     $\begin{aligned}\displaystyle i_s(t) \to I_s(s) \\ u_s(t) \to U_s(s) \end{aligned}$

外部约束的s域模型

1. 节点 – KCL $\sum i(t) = 0 \to \sum I(s) = 0$
2. 回路 – KVL $\sum u(t) = 0 \to \sum U(s) = 0$

7.1.2. 电路系统的 s 域分析方法

• 思路：
  1. 时域电路 $\to$ s域模型
     • $i_k(t), u_k(t) \to I_k(s), U_k(s)$
  2. s域电路 使用分析方法
     • 线性叠加原理、节点法、网孔法。。。
     • 求出 $I_K(s), U_k(s)$
  3. 取拉普拉斯反变换
     • 求 $i_k(t), u_k(t)$

---

7.2. 系统函数

7.2.1. 复频域分析

• 时域分析

$f(t) \to \boxed{h(t)} \to y(t)= f(t) \star h(t)$

• 复频域分析

$F(s) \to \boxed{H(s)} \to Y(s)= F(s)\cdot H(s)$

7.2.2. 微分方程的变换解

• $n$ 阶系统的微分方程:
  $\sum^{n}_{i=0} \alpha_i y^{(i)} (t) = \sum^{m}_{j=0} \beta_j f^{(j)} (t)$

  • 系统初始状态为 $y(0_-, y^{(1)}(0_-), \cdots, y^{(n-1)}(0_-)$

• 使用拉普拉斯变换微分特性:
  $\begin{aligned}y^{(i)} &\longleftrightarrow &s^i Y(s) - &\sum^{i-1}_{p=0} s^{i-1-p} y^{(p)} (0_-)\\ \sum^{n}_{i=0} \alpha_i y^{(i)} (t) &\longleftrightarrow &\big[\sum^{n}_{i=0}a_i s^i\big]Y(s) - &\sum^{n}_{i=0}a_i \big[\sum^{i-1}_{p=0}s^{i-1-p} y^{(p)}(0_-)\big]\end{aligned}$

• 若 $f (t)$ 在 $t = 0$ 时接入系统，则
  $\begin{aligned}f^{(n)}(t) &\longleftrightarrow s^n F(s) \\ \sum^{m}_{j=0} \beta_j f^{(j)} (t) &\longleftrightarrow \big[\sum^{m}_{j=0}b_j s^j\big]F(s)\end{aligned}$

• 求得:
  $\big[\sum^{n}_{i=0}a_i s^i\big]Y(s) - \sum^{n}_{i=0}a_i \big[\sum^{i-1}_{p=0}s^{i-1-p} y^{(p)}(0_-)\big] = \big[\sum^{m}_{j=0}b_j s^j\big]F(s)$

  $\begin{aligned}Y(s) & = \displaystyle \overset{{\color{blue}Y_{zi}(s)}}{\displaystyle\frac{\displaystyle\sum^{n}_{i=0}a_i \big[\displaystyle\sum^{i-1}_{p=0}s^{i-1-p} y^{(p)}(0_-)\big]}{\displaystyle\sum^{n}_{i=0}a_i s^i}} + \overset{{\color{blue}Y_{zs}(s)}}{\displaystyle\frac{\displaystyle\sum^{m}_{j=0}b_j s^j}{\displaystyle\sum^{n}_{i=0}a_i s^i}F(s)} \\ & = \displaystyle \frac{M(s)}{A(s)} + \frac{B(s)}{A(s)}F(s)\end{aligned}$

  ${\color{blue} Y_{zi}(s) + Y_{zs}(s) = Y(s) \to y(t) = y_{zi}(t) + y_{zs} (t) }$

• 步骤 :

  1. 方程式两边取 $\mathfrak{L}$
  2. 解出 $Y(s) = Y_{zi}(s)+ Y_{zs}(s)$
  3. 取 $\mathfrak{L}^{-1} \to y(t)$

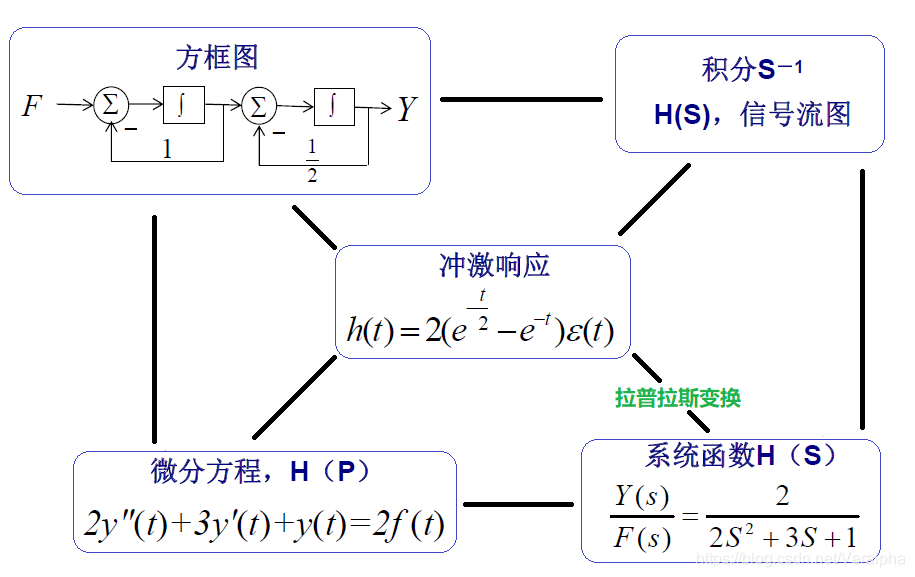
7.2.3. 连续系统函数 H

• 系统函数 $H(s)$ 定义:
  $H(s) \overset{\text{def}}{=} \frac{Y_{zs}(s)}{F(s)} = \frac{B(s)}{A(s)}$
  • 它只与系统的结构、元件参数有关，与激励、初始状态无关。

$y_{zs}(t) = h(t) \star f(t) \to Y_{zs}(s) = \mathfrak{L}\big[h(t)\big]\cdot F(s)$
$H(s) = \mathfrak{L}\big[h(t)\big]$

• 连续系统不同描述方法的关系
  

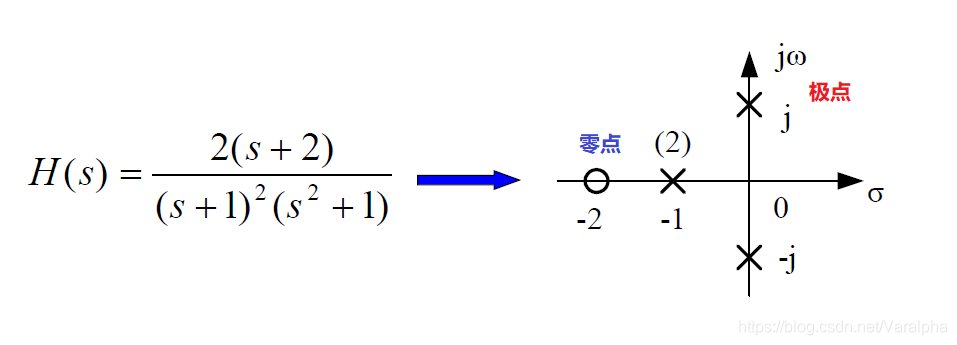
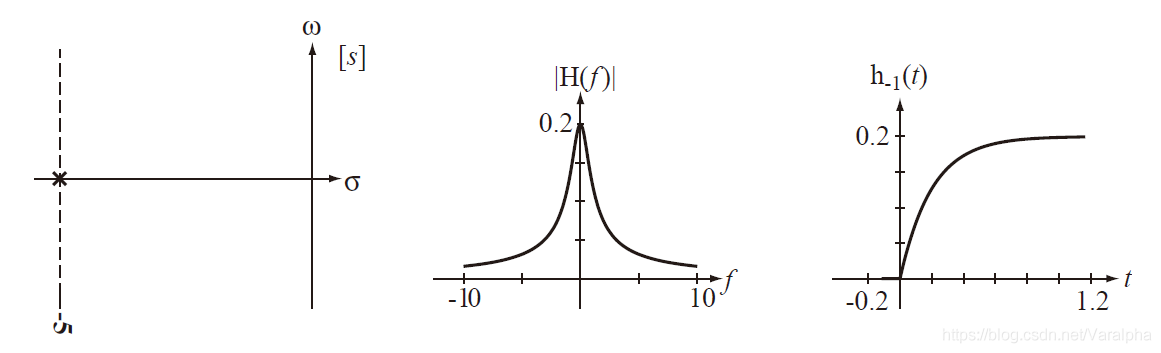
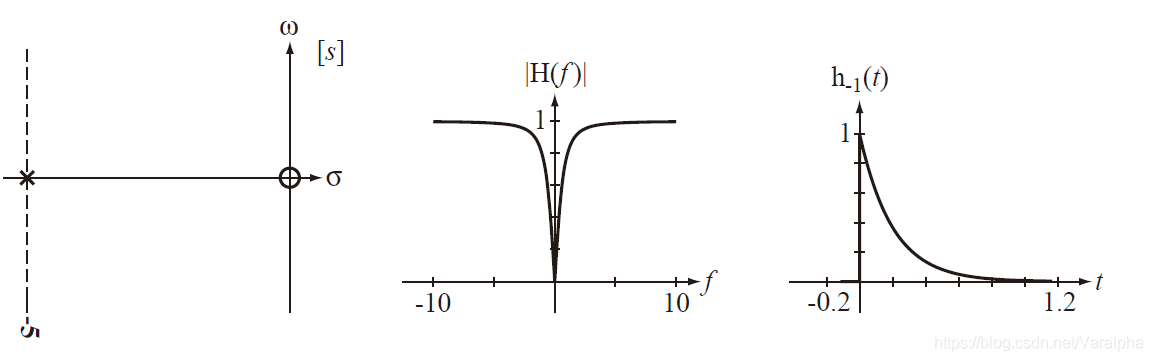
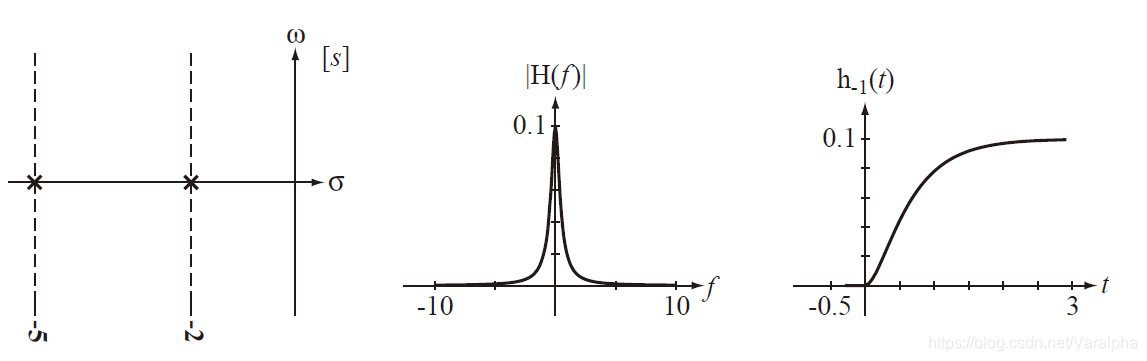
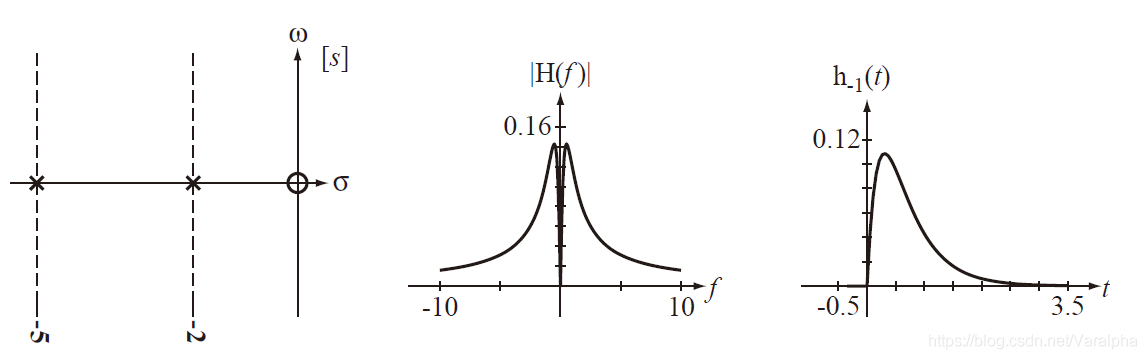
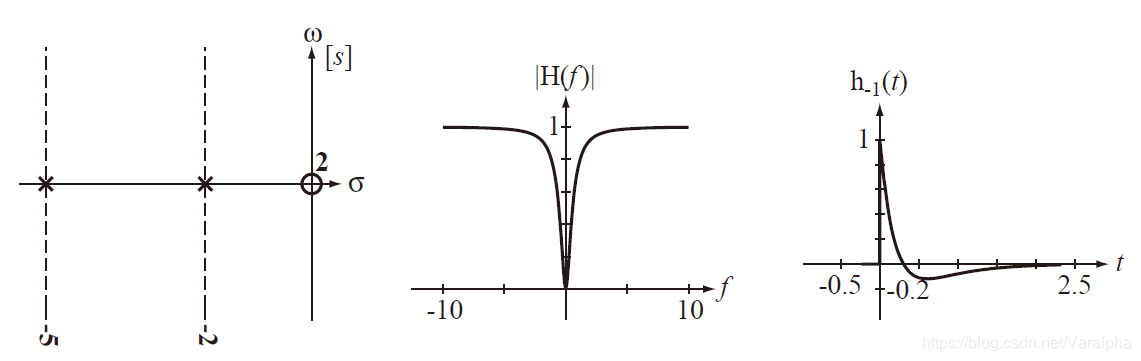
7.2.4. H 零极点分布与时域特性

• 系统函数的零点与极点

  • TI连续系统的系统函数是复变量s的有理分式，即：
    $H(s) = \frac{B(s)}{A(s)}$
  • $A(s) = 0$ 的根 $p_1, p_2, \cdots, p_n$ 称为系统函数 $H(s)$ 的极点；
  • $B(s) = 0$ 的根 $\zeta_1, \zeta_2, \cdots, \zeta_n$ 称为系统函数 $H(s)$ 的零点；
  • 将零极点画在复平面上 – 零极点分布图。
    

• 系统函数 $H(s)$ 与时域响应 $h(t)$

  • 以下讨论的系统均为连续因果系统中:
  • $H(s)$ 按其极点在 $s$ 平面上的位置可分为: 在 左半开平面、虚轴和右半开平面三类。

1. 极点在 左半开平面
   a. 若系统函数有负实单极点 $p= –\alpha(\alpha>0)$ ，则 $A(s)$ 中有因子 $(s+\alpha)$ ，其对应的响应函数为 $K e^{-\alpha t}\varepsilon(t)$
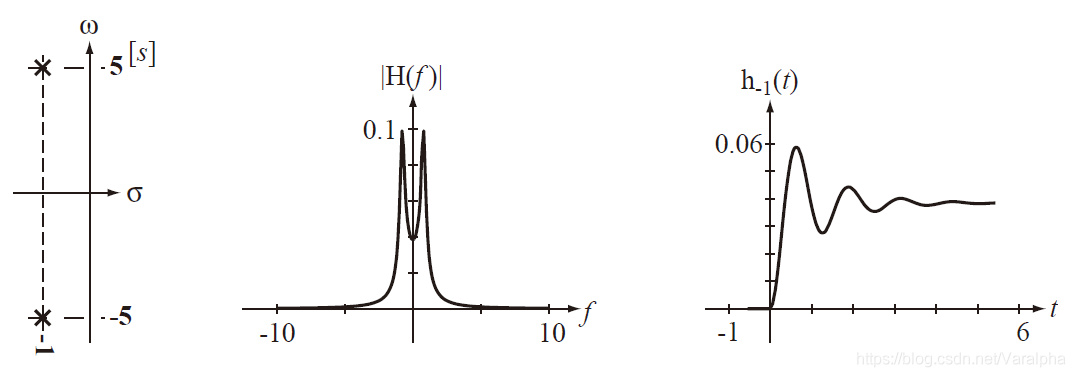
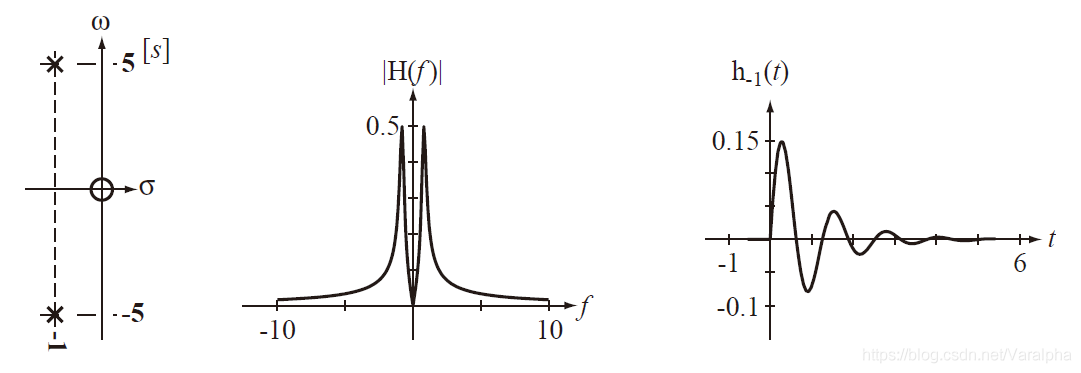
   b. 若有一对共轭复极点 $p_{12}= -\alpha\pm j\beta$ ，则 $A(s)$ 中有因子
   $[(s+\alpha)^2 + \beta^2] \leftrightarrow K e^{-\alpha t} \cos (\beta t + \theta) \varepsilon(t)$
   c. 若有 $r$ 重极点, 则 $A(s)$ 中有因子 $(s+\alpha)^r$ 或 $[(s+\alpha)^2+\beta^2]^r$ ，其响应为
   $K_i t^i e^{-\alpha t} \varepsilon(t)\; 或 \; K_i t^i e^{-\alpha t} \cos (\beta t + \theta) \varepsilon(t) ,\; _{(i=0,1,2,\cdots, r-1)}$
   以上三种情况：当 $t→\infty$ 时，响应均趋于 $0$ ，属暂态分量。

2. 极点在 虚轴上
   a. 单极点 $p=0$ 或 $p_{12}=±j\beta$，则响应为 $K\varepsilon(t)$ 或 $K\cos(\beta t+\theta)\varepsilon(t)$ — 稳态分量
   b. $r$ 重极点，相应 $A(s)$中有 $s^r$ 或 $(s^2+\beta^2)^r$ ，其响应函数为 $t^i\varepsilon(t)$ 或 $K_i t^i \cos(\beta t+\theta)\varepsilon(t),\; _{(i=0,1,2,…,r-1)}$ — 递增函数

3. 在 右半开平面：
   a. 均为递增函数。 (不稳定)

• 结论：LTI连续因果系统 $h(t)$ 的函数形式由 $H(s)$ 的极点确定，零点影响 $h(t)$ 的幅度、相位。

  1. $H(s)$ 在左半平面的极点所对应的响应函数为衰减的。 即当 $t→\infty$ 时，响应均趋于 $0$ 。
  2. $H(s)$ 在虚轴上的一阶极点所对应的响应函数为阶跃函数或者正弦函数。
  3. $H(s)$ 在虚轴上的高阶极点或右半平面上的极点，其所对应的响应函数都是递增的。

• 单极点无零
  

• 单极点单零
  

• 双极点无零
  

• 双极点单零
  

• 双极点双零
  

• 双极点共轭无零
  

• 双极点共轭单零
  

• 双极点共轭双零
  

7.2.5 连续系统稳定性判别

• 连续系统稳定的充分必要条件是:
  $\int^{-\infty}_{-\infty} \lvert h(t) \rvert dt \leq M$

  • 若 $H(s)$ 的收敛域包含虚轴，则该系统必是稳定系统。

• 连续因果系统稳定的充分必要条件是:
  $\int^{-\infty}_{0} \lvert h(t) \rvert dt \leq M$
  系统左半开平面的极点对应的响应为衰减函数，若 $H(s)$ 的极点均在左半开平面，则该系统必是稳定的因果系统。

• 系统稳定:

  1. 绝对可积分
  2. 收敛域包含虚轴 --> 所有极点均在左半开平面
     • $\mathcal{Re} [s] > \sigma_0, \; (\sigma_0 < 0)$

• 稳定系统的 s 域判别方法：

  1. 必要条件:
     $H(s) = \frac{B(s)}{A(s)}$
     $A(s) = a_ns^n + a_{n-1}s^{n-1} + \cdots + a_1s + a_0$
     若系统稳定，则 $a_i > 0,\; i =0,1,2,3,\cdots ,n$
  2. 充分必要条件:
     
     • 霍尔维茨准则(罗斯阵列、 R—H排列) Routh Criterion
     • 若罗斯阵列的第一列元素 ( 第一行至 $n+1$ 行 ) 的符号相同 ( 全为 “+”号或全为 “-”号 )，则 $H(s)$ 的极点全部在左半平面，系统稳定。
     • 特例:
       1. 倒序排列
       2. 前面为零，引入无穷小量 $0\to \delta$
       3. 全零行，引入一个辅助多项式（幂求导）->虚轴有根
     • 符号改变几次，右半平面就有几个根

7.2.6. Python 绘制零极点图、判断稳定

• 利用 Python 画出系统
  $H(s) = \frac{s^2+4s +3}{s^4+3s^3+4s^2+6s +4}$
  的零极点图，并判断系统的稳定性。

    # 导入 需要的 library 库  
    import numpy as np # 科学计算
    import matplotlib.pyplot as plt # 画图工具
    import control
    
    # 用 Python 表示 
    a, b = [1,3,4,6,4],[1,4,3] # 函数的分母 分子系数
    sys = control.tf(b,a)
    control.rlocus(sys,ylim=(-1.5,1.5));

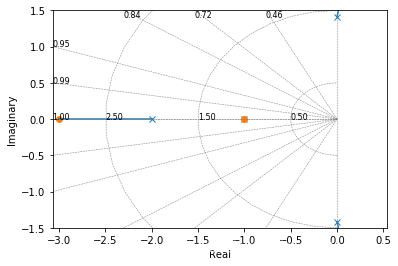
• 系统的零极图，如图所示，可见系统有4个极点，2个零点，其中在虚轴上有一对共轭极点，故该系统是不稳定的。

7.2.7. 系统函数

• 系统函数 $H(s)$ 与 $H(j\omega$

1. 设 $h(t)$ 为因果信号
   $H(s) = \int^{\infty}_{0_-}h(t)e^{-st} dt, \; \sigma>\sigma_0$
   $H(j\omega) = \int^{\infty}_{-\infty} h(t) e^{-j\omega t} dt = \int^{\infty}_{0_-} h(t)e^{-j\omega t} dt$
   • 当 $\sigma>\sigma_0$ 且 $\sigma_0<0$ 时( $H(s)$ 极点在左半平面)
     $H(j\omega) = H (s)\big\vert_{s=j\omega}$
   • 这种情况下，h(t) 对应的系统称为因果稳定系统
2. $H(s)$ 零、极点与连续系统频率特性
   • 设
     $H(s) = \frac{b_m (s-\zeta_1)\cdots (s-\zeta_m)}{(s-p_1)\cdots (s-p_n)}$
   • 若 $H(s)$ 极点均在左半开平面，则
     $H(j\omega) = H (s)\big\vert_{s=j\omega}$
     $H(j\omega)$ 又称为系统的频率响应
     $\begin{aligned}H(s) &= \frac{b_m (j\omega-\zeta_1)\cdots (j\omega-\zeta_m)}{(j\omega-p_1)\cdots (j\omega-p_n)}\\& = \displaystyle\frac{b_m \displaystyle\prod^{m}_{i=1}(j\omega - \zeta_i)}{\displaystyle\prod^{n}_{i=1}(j\omega-p_i)} \end{aligned}$
     设
     $\begin{aligned}j\omega - \zeta_i = B_i e^{j\psi_i},\; &i =1,2,3,\cdots , m \\j\omega - p_i = A_i e^{j\theta_i},\; &i =1,2,3,\cdots , n \end{aligned}$
     则
     $\begin{aligned}H(s) &= \frac{b_mB_1B_2\cdots B_me^{j(\psi_1+\psi_2+\cdots+\psi_m)}}{A_1A_2\cdots A_ne^{j(\theta_1+\theta_2+\cdots+\theta_m)}} \\ & = H(\omega)e^{j\phi(\omega)}\end{aligned}$
     $H(\omega) = \frac{b_mB_1B_2\cdots B_m}{A_1A_2\cdots A_n}$
     $\phi(\omega) = (\psi_1+\psi_2+\cdots+\psi_m)-(\theta_1+\theta_2+\cdots+\theta_m)$

7.2.8. Python 求频率响应函数，判断稳定

• 已知系统函数
  $H(s) = \frac{1}{s^3+2s^2+3s +1}$
  画出其零极点分布，求系统的单位冲激响应 $h(t)$，和频率响应 $H(j\omega)$ ，并判断系统是否稳定。

• 零极点分布

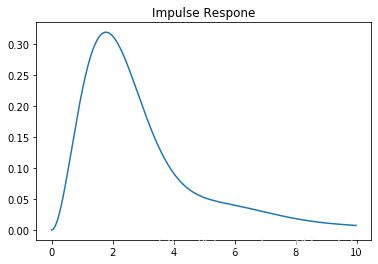
    a, b = [1,2,3,1],[1] # 分母 分子系数
    sys = control.tf(b,a)
    control.rlocus(sys,ylim=(-1.5,1.5),xlim=(-0.8,0),grid=False);

• 单位冲激响应

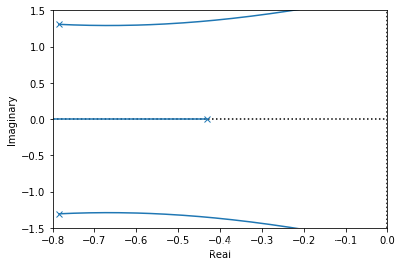
    t = np.arange(0,10,0.02)
    h = control.impulse_response(sys,t)
    plt.plot(h[0],h[1])
    plt.title('Impulse Respone')
    plt.show()

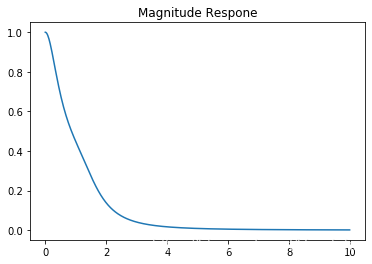
    freq = control.freqresp(sys,t)
    plt.plot(freq[2],freq[0][0][0])
    plt.title('Magnitude Respone')
    plt.show()

• 频率响应
  

To TOP 至目录