图的概念及种类
图的概念
图是互连结点的集合
如图所示,一个图可能是这样:
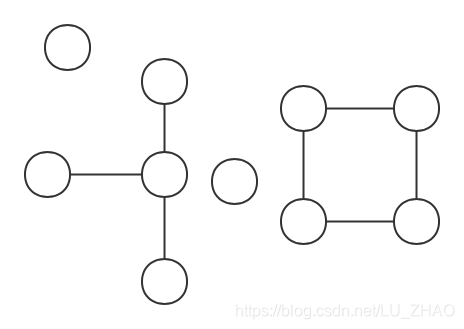
图有结点(node)和边(Edge)。节点之间通过边互相连接。
二元组的定义
图G是一个有序二元组(V, E),其中V称为顶集(Vertices Set),E称为边集(Edges set),E与V不相交。它们亦可写成V(G)和E(G)。
图的种类
有向图和无向图
如果给图的每条边规定没有方向,那么得到的图称为无向图。
在图中,若用箭头标明了边是有方向性的,从起点到终点,则称这样的图为有向图。
如上图中,G1为无向图,G2为有向图。
图G1:

图G2:
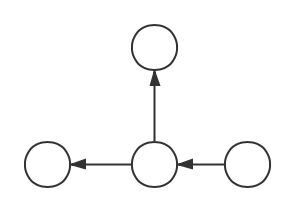
DAG
回路指的是从一个点出发经过其他的点后有回到原点,比如下面的图从A点出发向B经C可回到A,形成一个回路:
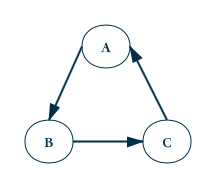
有向无环图(Directed Acyclic Graph)指的是一个无回路的有向图。:


AOV
顶点活动网(Activity On Vertex Network)指的是在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系。这样的有向图为顶点表示活动的网。
完全图
n个顶点,n(n-1)/2条边且没有重复边和环的图,称为完全无向图。
具有n个顶点,n(n-1) 条边的有向图,称为完全有向图。
完全无向图和完全有向图都称为完全图。
欧拉图
欧拉图(Euler Graph)指的是通过连通图 G = < V, E >(无向图或有向图)中所有边且每边仅通过一次通路,相应的回路称为欧拉回路。
具有欧拉回路的图称为欧拉图,具有欧拉通路而不具有欧拉回路的图叫半欧拉图。
- 一个无向图G是欧拉图当且仅当G是连通的,且无奇度顶点。
- 一个有向图D是欧拉图当且仅当D是连通的,且所有顶点的入度等于出度。
哈密顿图
哈密顿图(Hamilton Graph)通过在G = < V, E >中,G中经过每一个顶点一次且仅一次的通路称为哈密尔顿通路,经过每一个顶点一次且仅一次的回路称为哈密尔顿回路。
具有哈密尔顿回路的图称为哈密尔顿图,具有哈密尔顿通路而不具有哈密尔顿回路的图称为半哈密尔顿图。
暂无哈密尔顿图的简单充要条件,寻找充要条件是图论中的一个难题。
美国图论数学家奥勒在1960年给出了一个图是哈密尔顿图的充分条件:对于顶点个数大于2的图,如果图中任意两点度的和大于或等于顶点总数,那这个图一定是哈密顿图。
连通图
连通图(Connected Graph)指的是图中任意两个结点都是连通的。连通指的是在图G = < V, E >中,若从顶点i到顶点j有路径相连,则称i和j是连通的。

强连通图
强连通图(Strongly Connected Graph)指的是在图G = < V, E >是连通图,且此图是有向图。

