图(一)图的概念及图的存储结构

图的基本概念

图是由(V, E)来表示的，对于无向图来说，其中 V = (v0, v1, … , vn)，E = { (vi,vj) (0 <= i, j <= n且i 不等于j)}，对于有向图，E = { < vi,vj > (0 <= i, j <= n且i 不等于j)}。V是顶点的集合，E是边的集合。
1、定义：图G由以下两种集合构成。

有限个顶点构成的非空集合V(G)
有限条边构成的集合E(G)

2、无向图与有向图

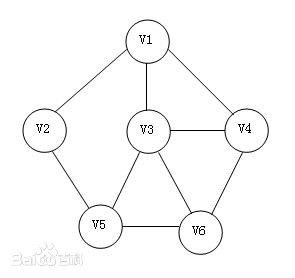
无向图
边没有方向的图称为无向图(每一条边均可利用无序的顶点对表示)。
无向图G=<V,E>,其中：
1.V是非空集合，称为顶点集。
2.E是V中元素构成的无序二元组的集合，称为边集。
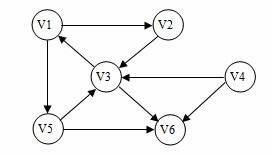
有向图
有向图是这样的一种图，它的每一条边均
可利用有序的顶点对表示。
◆ 例如：利用<V0,V1> 表示有向边（箭头）
其中：V0称为尾(Tail)，V1称为头(Head)

3、完全图与子图
完全图
定义：具有最大边数的图(不能再添加)
任意两个顶点之间至少有一条边。
无向完全图的最多边数：n(n-1)/2
有向完全图的最大边数：n(n-1)

子图：
如果：V(G’)⊆V(G) and E(G’)⊆E(G)
则称：G’是G的子图

4、顶点的度
依附于该顶点的边的数目

对于有向图，度进一步地细分为入度和出度。
(1)以顶点v为头的边的数目成为v的入度,顶点的入边条数称为该顶点的入度，记为ID(V).
(2)以顶点v为尾的边的数目成为v的出度，顶点的出边条数称为该顶点的出度记为OD(V).
(3)顶点v的度为TD(V)=ID(V)+OD(V).

性质： 一般地，若顶点Vi的度记为TD(Vi)，那么一个有n个顶点，e条边或弧的图，满足如下的关系。
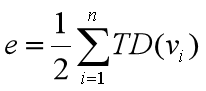
在这里插入图片描述

5、路径(Path)
无向图中从顶点V到顶点V的路径是一个顶点序列(V=Vi,0 Vi,1 ，Vi,2 ，Vi,3 ，…，Vi,m=V)
其中：(Vi,j-1，Vi,j)∈E,1≤j≤m
推广到：有向图的路径
路径长度：路径经过的边数

简单路径
序列中顶点不重复出现的路径
回路（环）
起点和终点相同的路径
简单回路（简单环）
除了起点和终点，其余顶点不重复出现的回路

性质：
在这里插入图片描述
6、连通图

顶点v到顶点v是连通的，当且仅当存在一条从顶点v到顶点v的路径
如果对于图G的任意两个顶点v和v*，v到v*均是连通的，则称图G是连通的

连通分量：无向图 G的一个极大连通子图称为 G的一个连通分量（或连通分支）。连通图只有一个连通分量，即其自身；非连通的无向图有多个连通分量。

性质：
任何连通图的连通分量只有一个，就是它本身(否则不是极大)。
在这里插入图片描述

7、生成树

定义：一个连通图的生成树是一个极小连通子图，它含有图中的全部顶点，但只有足以构成一棵树的n-1条边。
极小：不能再减少。
性质：如果一个图有n个顶点和小于n-1条边，则是非连通图，如果有n个顶点和多于n-1条边，则一定有环
性质:反之不然。
如果有n个顶点和n-1条边，不一定是生成树（反例)。

图的存储结构

1、邻接矩阵——表示顶点之间相邻关系的矩阵。(顺序存储结构)

一个具有n(n≥1)个顶点的图G，它的邻接矩阵是一个n×n的矩阵，记为adj_mat
其中：
adj_mat[i][j]=1，如果i和j邻接
adj_mat[i][j]=0，如果i和j不邻接

由临接矩阵的行数或列数可知图中的定点数。

无向图：邻接矩阵是对称的，矩阵中“1”的个数为图中总边数的两倍，矩阵中的第i行或第i列的元素之和即为顶点i的度。

在这里插入图片描述

有向图：矩阵中的“1”的个数为图的边数，矩阵中第i行的元素之和即为顶点i的出度，第j列元素之和即为顶点j的入度。

在这里插入图片描述

推论：顶点Vi的度=第i行的元素之和+第i列的元素之和
有时图的边或弧具有与他相关的数，称权。
这种带权的图称为网。

邻接矩阵的结构型定义如下：

typedef struct
{
	int no;//顶点编号
	char info;//顶点其他信息
}VertexType;//顶点类型
typedef struct
{
	int edges[maxSize][maxSize];//邻接矩阵定义，如果有权图，则在此句中讲int改为float
	int n,e;//分别为顶点和边数
	VertexType vex[maxSize];//存放结点信息
}MGraph;

邻接矩阵表示的优缺点

优点：简单（Matlab工具箱）
缺点：时间复杂度=O(n2-n)=O(n2)

2、邻接表（图的一种链式存储结构

对图中的每一个顶点i建立一个单链表，每个单链表的第一个结点存放有关顶点的信息。

第i个单链表中的结点表示依附于顶点Vi的边(有向图是以顶点Vi为尾的弧)
在这里插入图片描述
单链表的普通结点由三个域组成：

邻接点域（adjvex）：与顶点vi邻接的点在图中的位置
链域（nextarc）：下一条边或弧的结点
数据域（info）：存储边或弧的相关信息（例如权值）

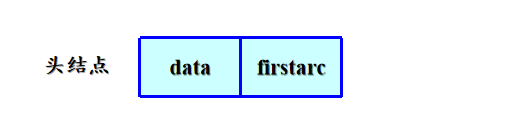
在这里插入图片描述

每一个链表附设一个头结点，由两个域构成：

数据域（data）: 存储顶点vi的名或其它有关信息
链域（firstarc）:指向单链表的第一个结点

例题：

已知无向图G含有16条边，其中度为4的顶点个数为3，度为3的顶点个数为4，其它顶点的度均小于3。那么，图G所含的顶点个数至少是（B）

A. 10
B. 11
C. 13
D. 15

解析：无向图边数的两倍等于各顶点度数的总和。由于其他顶点的度均小于3，可以设它们的度都为2，设它们的数量是x，可列出这样的方程43+34+2x=162，解得x=4。4+3+3=11

下列关于无向连通图特性的叙述中，正确的是(A)
Ⅰ. 所有顶点的度之和为偶数
Ⅱ. 边数大于顶点个数减一
Ⅲ. 至少有一个顶点的度为1
A. 只有Ⅰ B. 只有Ⅱ C. Ⅰ和Ⅱ D. Ⅰ和Ⅲ

解析：
Ⅰ．每条边都连接了两个结点，则在计算顶点的度之时，这条边都被计算了两次，故所有顶点的度之和为边数的两倍，显然必为偶数。
Ⅱ．边数大于顶点个数减1，如果定点数为3，则边数为2，边数=定点个数减1；
Ⅲ．在顶点数n≥3的完全有向图中，没有度为1的节点。

若无向图 G中含7个顶点，要保证图G在任何情况下都是连通的，则需要的边数最少是（C）
   A. 6   
   B. 15
   C. 16  
   D. 21

解析：要保证无向图G在任何情况下都是连通的，即任意变动图G中的边，G始终保持连通，首先需要G的任意6个结点构成完全连通子图G1，需15条边，然后再添一条边将第7结点与G1连接起来，共需16条边。

含有n个顶点的连通无向图，其边的个数至少为(A).
A.n-1
B.n
C.n+1
D.nlogn

解析：一个连通图边数最少的情况就是这个图中没有回路的请款，实际上这个图是一棵树，对于树，分支和结点的关系为：分支树比结点数少1.

一个有n个结点的无向图，最少有（B）个连通分量，最多有(D)个连通分量。
A.0
B.1
C.n-1
D.n

由邻接矩阵A=（010）可以看出，该图共有①中的()个顶点；如果是有向图，该图共有②中()条边；如果是无向图，则共有③中的()条边。
            101
            010

①：A.9
B.3
C.6
D.1
E.以上答案不正确
②：A.5
B.4
C.3
D.2
E.以上答案不正确
③：A.5
B.4
C.3
D.2
E.以上答案不正确

解析：BBD
对于邻接矩阵，行数或者列数代表所表示的图的顶点数
邻接矩阵如果是对称的，则它表示的即可能是有向图，又可能是无向图。
表示有向图的时候，邻接矩阵中1的个数就是有向图中的边数；
表示无向图的时候，邻接矩阵中1的个数正好是图中边数的2倍。