梯度与方向导数基本概念

举例来说，设函数 $y=f(x,y) =e^{-x^2 - y^2}$，其函数图形如下所示。
其在点P $(x_0, y_0)$ 方向导数为
$\nabla f(x_0, y_0) = \frac{\partial f}{\partial x}\overrightarrow{i} + \frac{\partial f}{\partial y}\overrightarrow{j} {\partial y}\overrightarrow{j} = -2x_0e^{-x_0^2 - y_0^2}\overrightarrow{i} -2y_0e^{-x_0^2 - y_0^2}\overrightarrow{j}$

这样我们就可以求得P在任意方向上的方向导数。其几何含义就是 $f$ 在点P的变化速率。当曲面不是平面的时候，每个方向上的变化率是不一样的。如下图所示，在点P，其梯度就是在各个方向的变化。

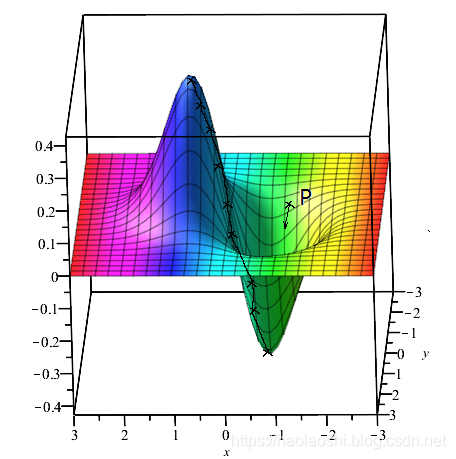
再看另外的一个示例（原文 或 引用），在这个示例中，如果要到达两个最低点（如下图所示），可以有两条不同的路径。这两条路径是最短路径，条件就是路径上的每点都是方向导数最小的点。