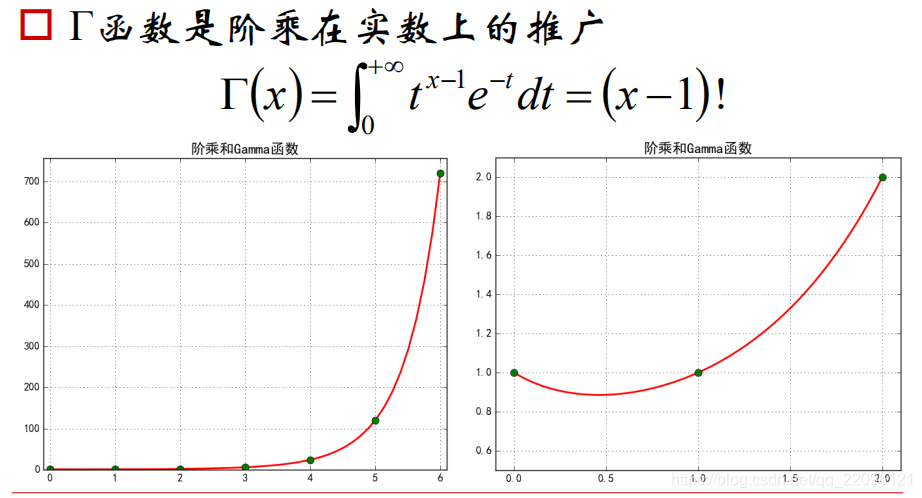
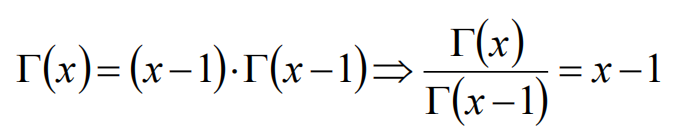对数函数的的上升速度
我们容易知道,对数函数虽然底数不同但都是经过点(1,0),但经过时斜率不同,是否能够试图找出经过点(1,0)时斜率为1时的对数函数的底数?
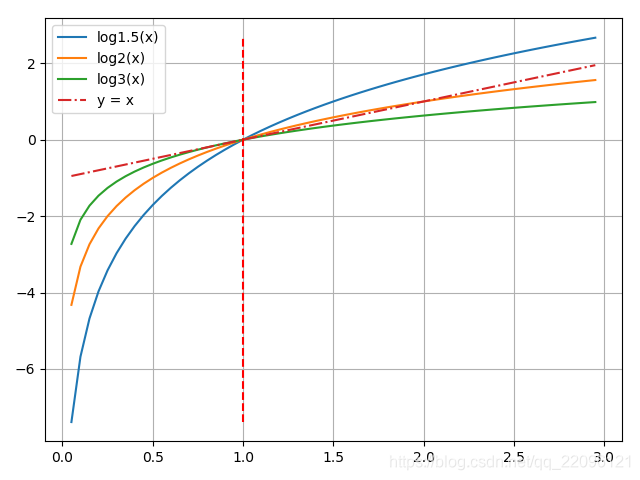
问题分析:
-
令
-
则:
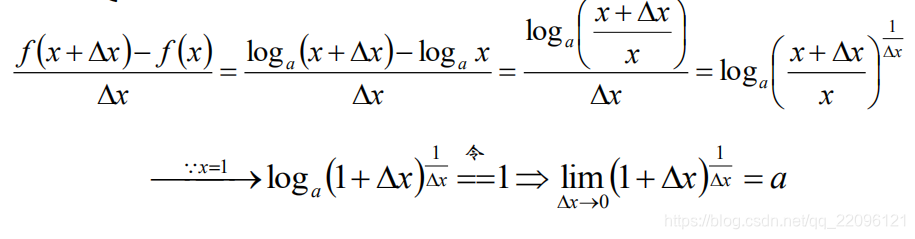
-
问:
-
构造数列
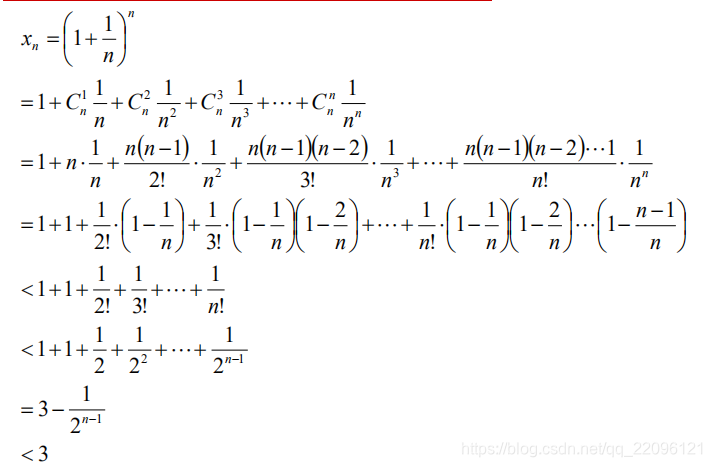
-
自然常数
根据前文中二项展开,已经证明数组 单增有上界,因此必有极限记作
同时:
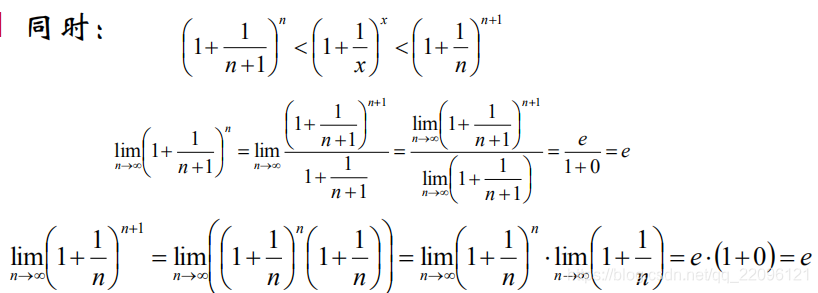
根据夹逼准则,函数
的极限存在,为
导数
- 导数就是曲线的斜率。
- 二阶导数是斜率变化快慢的反应,表征曲线凹凸性。
- 根据 可以得到函数 的导数,进一步根据旱地公式、反函数求导等,得到其他初等函数的导数。
常用函数的导数

导数的应用
1. 求解
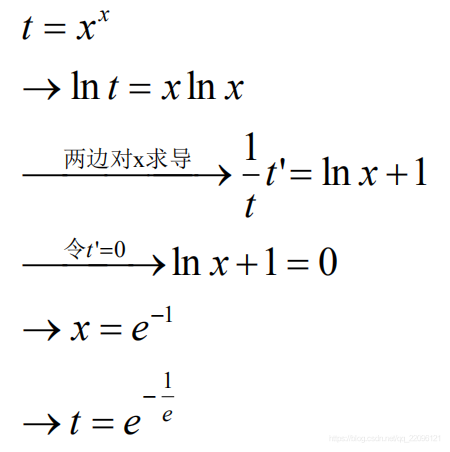

2. Taylor公式 - Maclaurin公式
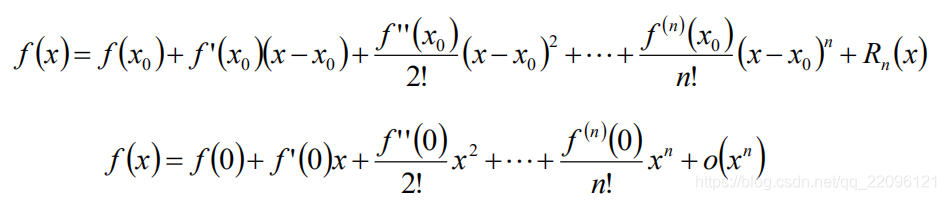
Taylor公式的应用1
- 数值计算:初等函数值的计算(在原点展开)
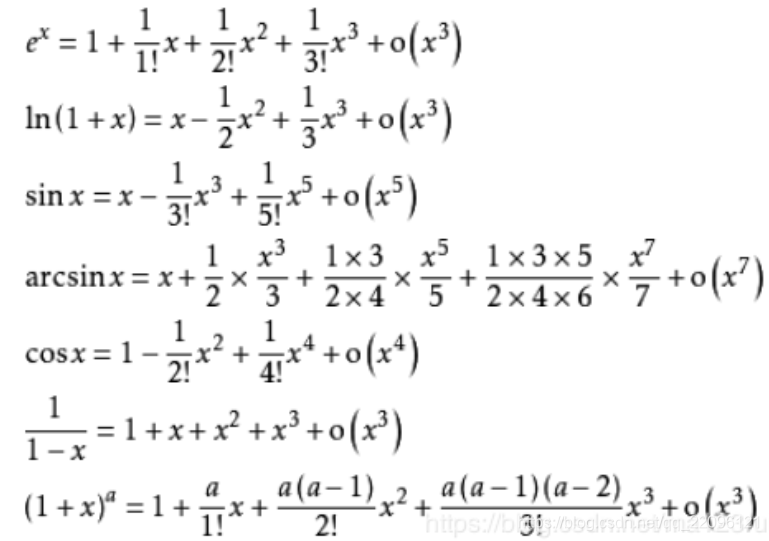
- 在实践中,往往需要做一定程度的变换
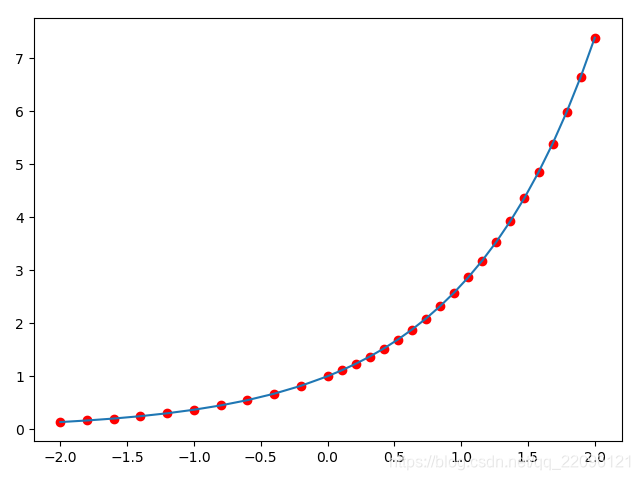
Taylor公式的应用:计算

import numpy as np
import matplotlib.pyplot as plt
# 应用Taylor处理小数部分
def calc_e_small(r):
print('r', r)
# Taylor展开10项
n = 10
# 1 ~ n 的阶乘组成的array
f = np.arange(1, n + 1).cumprod()
print('f', f)
# n个r组成array
g = np.array([r] * n)
print('g', g)
# r的1~n次方
b = g.cumprod()
print('b', b)
# e的n项Taylor展开
return np.sum(b / f) + 1
def calc_e(x):
'''
e^x = 2^k * e^r |r| <= 0.5 * ln2
'''
reverse = False
if x < 0:
x = -x
reverse = True
ln2 = 0.69314718055994530941723212145818
c = x / ln2
k = int(c + 0.5)
r = x - k * ln2
y = (2 ** k) * calc_e_small(r)
if reverse:
return 1 / y
return y
t1 = np.linspace(-2, 0, 10, endpoint=False)
t2 = np.linspace(0, 2, 20)
t = np.concatenate((t1, t2))
# print(t)
y = np.empty_like(t)
for i, x in enumerate(t):
y[i] = calc_e(x)
plt.plot(t, y, 'ro')
plt.plot(t, np.e ** t)
plt.show()
2.
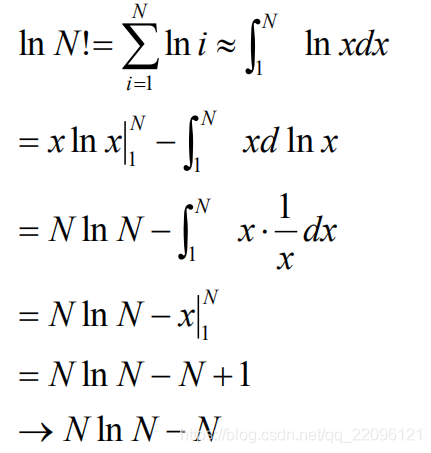
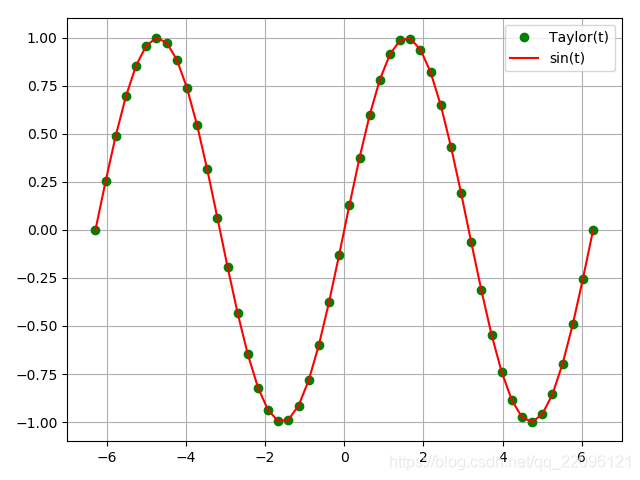
Taylor应用:计算sin
import numpy as np
import matplotlib.pyplot as plt
def calc_sin_small(x):
x2 = -x ** 2
t = x
f = 1
sum = 0
for i in range(10):
sum += t / f
t *= x2
f *= ((2 * i + 2) * (2 * i + 3))
return sum
def calc_sin(x):
a = x / (2 * np.pi)
k = np.floor(a)
a = x - k * 2 * np.pi
return calc_sin_small(a)
t = np.linspace(-2 * np.pi, 2 * np.pi)
y = np.empty_like(t)
for i, x in enumerate(t):
y[i] = calc_sin(x)
plt.xlim((-7, 7))
plt.ylim((-1.1, 1.1))
plt.plot(t, y,'go',label='Taylor(t)')
plt.plot(t,np.sin(t),'r-',label='sin(t)')
plt.grid(True)
plt.legend()
plt.show()
方向导数
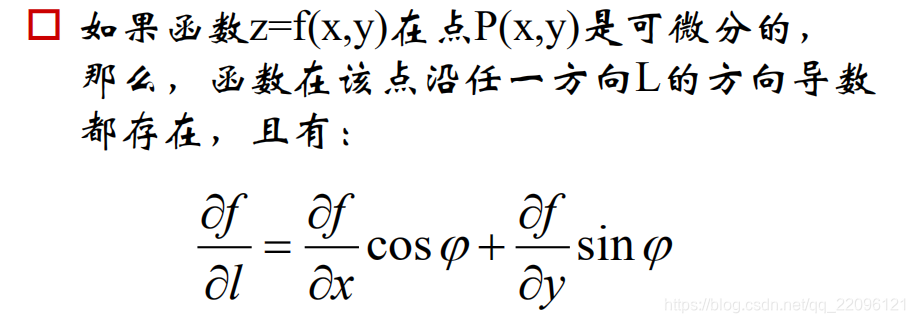
其中, 为x轴到L的转角
梯度

函数
证明过程:使用分部积分推导