一、概述
我们知道,机器学习的特点就是:以计算机为工具和平台,以数据为研究对象,以学习方法为中心;是概率论、线性代数、数值计算、信息论、最优化理论和计算机科学等多个领域的交叉学科。所以本文就先介绍一下机器学习涉及到的一些最常用的的数学知识。
二、线性代数
2-1、标量
一个标量就是一个单独的数,一般用小写的的变量名称表示。
2-2、向量
一个向量就是一列数,这些数是有序排列的。用过次序中的索引,我们可以确定每个单独的数。通常会赋予向量粗体的小写名称。当我们需要明确表示向量中的元素时,我们会将元素排
列成一个方括号包围的纵柱:
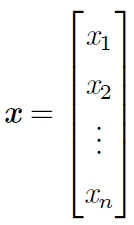
我们可以把向量看作空间中的点,每个元素是不同的坐标轴上的坐标。
2-3、矩阵
矩阵是二维数组,其中的每一个元素被两个索引而非一个所确定。我们通常会赋予矩阵粗体的大写变量名称,比如A。 如果一个实数矩阵高度为m,宽度为n,那么我们说。

矩阵这东西在机器学习中就不要太重要了!实际上,如果我们现在有N个用户的数据,每条数据含有M个特征,那其实它对应的就是一个N*M的矩阵呀;再比如,一张图由16*16的像素点组成,那这就是一个16*16的矩阵了。现在才发现,我们大一学的矩阵原理原来这么的有用!要是当时老师讲课的时候先普及一下,也不至于很多同学学矩阵的时候觉得莫名其妙了。
2-4、张量
几何代数中定义的张量是基于向量和矩阵的推广,通俗一点理解的话,我们可以将标量视为零阶张量,矢量视为一阶张量,那么矩阵就是二阶张量。
例如,可以将任意一张彩色图片表示成一个三阶张量,三个维度分别是图片的高度、宽度和色彩数据。将这张图用张量表示出来,就是最下方的那张表格:
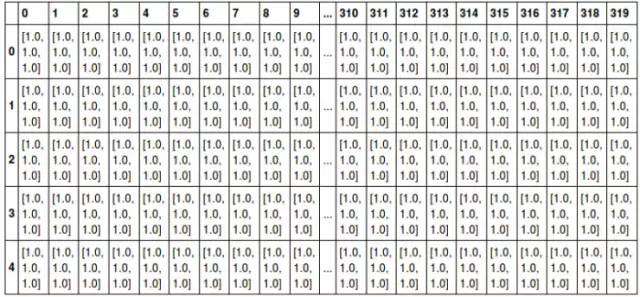
其中表的横轴表示图片的宽度值,这里只截取0~319;表的纵轴表示图片的高度值,这里只截取0~4;表格中每个方格代表一个像素点,比如第一行第一列的表格数据为[1.0,1.0,1.0],代表的就是RGB三原色在图片的这个位置的取值情况(即R=1.0,G=1.0,B=1.0)。
当然我们还可以将这一定义继续扩展,即:我们可以用四阶张量表示一个包含多张图片的数据集,这四个维度分别是:图片在数据集中的编号,图片高度、宽度,以及色彩数据。
张量在深度学习中是一个很重要的概念,因为它是一个深度学习框架中的一个核心组件,后续的所有运算和优化算法几乎都是基于张量进行的。
2-5、范数
有时我们需要衡量一个向量的大小。在机器学习中,我们经常使用被称为范数(norm) 的函数衡量矩阵大小。Lp 范数如下:
所以:
L1范数:为x向量各个元素绝对值之和;
L2范数:为x向量各个元素平方和的开方。
这里先说明一下,在机器学习中,L1范数和L2范数很常见,主要用在损失函数中起到一个限制模型参数复杂度的作用,至于为什么要限制模型的复杂度,这又涉及到机器学习中常见的过拟合问题。具体的概念在后续文章中会有详细的说明和推导,大家先记住:这个东西很重要,实际中经常会涉及到,面试中也常会被问到!!!
2-6、特征分解
许多数学对象可以通过将它们分解成多个组成部分。特征分解是使用最广的矩阵分解之一,即将矩阵分解成一组特征向量和特征值。
方阵A的特征向量是指与A相乘后相当于对该向量进行缩放的非零向量:
标量被称为这个特征向量对应的特征值。
使用特征分解去分析矩阵A时,得到特征向量构成的矩阵V和特征值构成的向量,我们可以重新将A写作:
2-7、奇异值分解(Singular Value Decomposition,SVD)
矩阵的特征分解是有前提条件的,那就是只有对可对角化的矩阵才可以进行特征分解。但实际中很多矩阵往往不满足这一条件,甚至很多矩阵都不是方阵,就是说连矩阵行和列的数目都不相等。这时候怎么办呢?人们将矩阵的特征分解进行推广,得到了一种叫作“矩阵的奇异值分解”的方法,简称SVD。通过奇异分解,我们会得到一些类似于特征分解的信息。
它的具体做法是将一个普通矩阵分解为奇异向量和奇异值。比如将矩阵A分解成三个矩阵的乘积:
假设A是一个mn矩阵,那么U是一个m
m矩阵,D是一个m
n矩阵,V是一个n
n矩阵。
这些矩阵每一个都拥有特殊的结构,其中U和V都是正交矩阵,D是对角矩阵(注意,D不一定是方阵)。对角矩阵D对角线上的元素被称为矩阵A的奇异值。矩阵U的列向量被称为左奇异向量,矩阵V 的列向量被称右奇异向量。
SVD最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。另外,SVD可用于推荐系统中。
2-8、Moore-Penrose伪逆
对于非方矩阵而言,其逆矩阵没有定义。假设在下面问题中,我们想通过矩阵A的左逆B来求解线性方程:
等式两边同时左乘左逆B后,得到:
是否存在唯一的映射将A映射到B取决于问题的形式。
如果矩阵A的行数大于列数,那么上述方程可能没有解;如果矩阵A的行数小于列数,那么上述方程可能有多个解。
Moore-Penrose伪逆使我们能够解决这种情况,矩阵A的伪逆定义为:
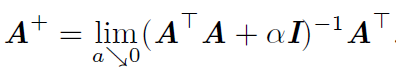
但是计算伪逆的实际算法没有基于这个式子,而是使用下面的公式:
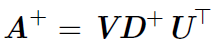
其中,矩阵U,D 和V 是矩阵A奇异值分解后得到的矩阵。对角矩阵D 的伪逆D+ 是其非零元素取倒之后再转置得到的。