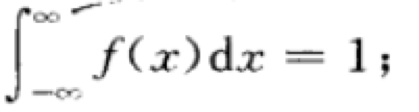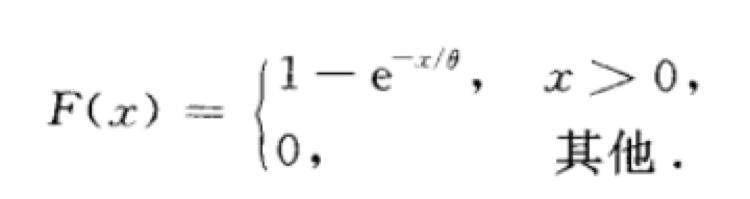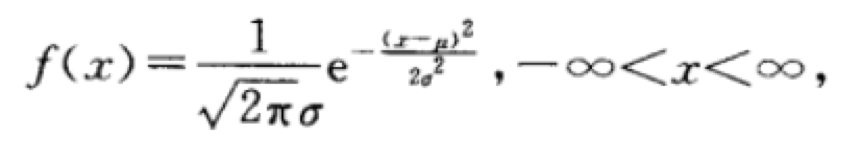机器学习数学基础(二)
前言
概率密度函数和分布函数是机器学习的回归中重要的基础。因此学习概率密度函数和分布函数很重要。
随机变量的定义
设随机试验样本空间为S={e}。X = X(e) 是定义在样本空间S上的实值单值函数。称X=X(e)为随机变量。也就是要求对于任意实数x,集合{e|X(e) =< x}有确定的概率。否则x没意义。
离散型随机变量
能取到有限个或可列无限多个的随机变量为离散型随机变量。
三种重要的离散型随机变量
以下这三种随机变量在机器学习分类中有应用。
1)0-1分布
设随机变量X只可能取0与1两个值,它的分布规律如下:
2)伯努利试验
伯努利试验(Bernoulli trial)是只有两种可能结果的单次随机试验,即对于一个随机变量X而言,本试验是由雅各布·白努利发明的。
将伯努利试验独立重复进行n次,则称这一串重复的独立试验为n重伯努利试验。二项分布就是重复n次独立的伯努利试验。
假设事件A在k次试验中发生,n-k次试验中A不发生的概率如下:
表示为
其中
伯努利试验与二项分布的关系
在概率论和统计学中,二项分布是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上,当n = 1时,二项分布就是伯努利分布。二项分布是显著性差异的二项试验的基础。
3)泊松分布(Poisson分布)
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。
设随机变量X所有可能的取值为0,1,2,…,取各个值的概率如下:
其中λ>0是常数,k=0,1,2,..
随机变量的分布函数
在实际应用中我们往往需要误差落在某个区间内的概率。因此我们需要了解随机变量的分布函数。
定义
设X是一个随机变量,x是任意实数,函数
称为X的分布函数。
性质
1) 分布函数是一个不减函数。
2) 0 =< F(x) =<1,且满足如下条件:
连续型随机变量及其概率密度
定义
对于随机变量X的分布函数F(X),存在非负函数f(x),对于任意实数x有:

则称X为连续型随机变量,其中函数f(x)称为X的概率密度函数,简称概率密度。
性质
1) f(x) >= 0。
2)
3) 对任意实数x1,x2(x1 =<x2)
4) 若f(x)在x点处连续,则有
三种重要的随机变量的概率密度
均匀分布的概率密度及分布函数
若连续型随机变量X具有概率密度如下:
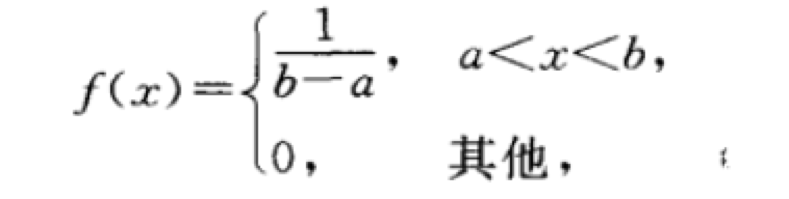
则称X在区间(a,b)上服从均匀分布。记为X~U(a,b)。
X的分布函数如下:
f(x)和F(x)的图像如下所示:
指数分布的概率密度及分布函数
若连续型随机变量X的概率密度如下所示:
其中θ>0为常数,则称X服从参数为θ的指数分布。
X的分布函数如下:
f(x)在θ=1/3 ,1,2的情况下的图像如下所示:

正态分布的概率密度及分布函数
若连续型随机变量X的概率密度如下所示:
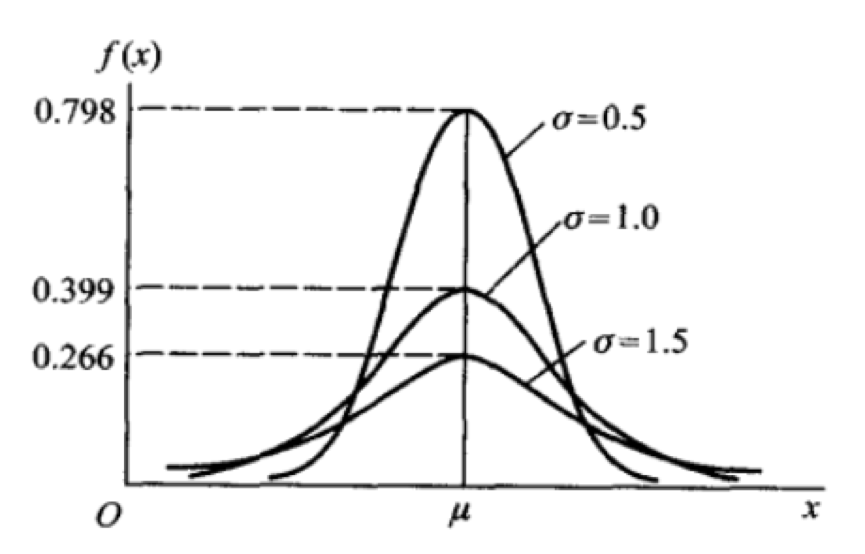
其中,μ,σ(σ>0)为常数,则称X服从参数为μ,σ的正态分布或高斯分布,记为X~N(μ,σ^2)。如果固定μ,改变σ,可以看出σ越小图形变得越尖,因而X落在μ附近的概率越大。如下图所示:
X 的分布函数如下所示:
参考文献
[1]. https://en.wikipedia.org/wiki/Binomial_distribution
[2]. https://en.wikipedia.org/wiki/Poisson_distribution
[3].《概率论与数理统计》浙江大学第四版。