机器学习 数学基础

1 线性代数

1.1 矩阵的意义

矩阵来源于方程组，矩阵的意义在矩阵的乘法，矩阵与向量相乘，等效于对向量进行线性变换

1.2 矩阵特征值和特征向量

$$\boldsymbol{A}\vec{x}=\lambda\vec{x}$$ 矩阵对特征向量进行线性变换，变化后的向量与特征向量保持平行

2. 微积分

首先需要注意的一点是，梯度应该是列向量

$$\nabla f(\vec{x}) =\frac{ \partial{f(\vec{x})} }{\partial{\vec{x}} } =(\frac{ \partial{f(\vec{x})} }{\partial{x_1} }, \frac{ \partial{f(\vec{x})} }{\partial{x_2} }, \cdots, \frac{ \partial{f(\vec{x})} }{\partial{x_n} })^T$$ Hessian矩阵与二阶导数密切相关
$$\nabla^2 f(\vec{x}) =\begin{bmatrix} \frac{ \partial{f(\vec{x})} }{\partial{x_1}^2} & \frac{ \partial{f(\vec{x})} }{\partial{x_1}\partial{x_2}} & \cdots & \frac{ \partial{f(\vec{x})} }{\partial{x_1}\partial{x_n}} \\ \frac{ \partial{f(\vec{x})} }{\partial{x_2}\partial{x_1}} & \frac{ \partial{f(\vec{x})} }{\partial{x_2}^2} & \cdots & \frac{ \partial{f(\vec{x})} }{\partial{x_2}\partial{x_n}} \\ \cdots & \cdots & \cdots & \cdots \\ \frac{ \partial{f(\vec{x})} }{\partial{x_n}\partial{x_1}} & \frac{ \partial{f(\vec{x})} }{\partial{x_n}\partial{x_2}} &\cdots&\frac{ \partial{f(\vec{x})} }{\partial{x_n}^2} \\ \end{bmatrix}$$

2.1 为什么梯度的方向是函数上升最快的方向

  这要从泰勒级数说起，泰勒级数只保留前两项的表达式为

$$f(\vec{x}+\vec{\delta}) =f(\vec{x}) +\nabla^T f(\vec{x})\vec{\delta}$$ 那么要想 $f(\vec{x}+\vec{\delta})$上升最快，需要 $\nabla^T f(\vec{x})\vec{\delta}$上升最快，由向量基础知识，我们可以知道， $\vec{\delta}$与 $\nabla f(\vec{x})$同方向时， $\nabla^T f(\vec{x})\vec{\delta}$上升最快。因此，才会有梯度的方向是函数上升最快的方向的结论。

2.2 为什么极大值和极小值的区分与Hessian矩阵（二阶导数）相关

  此外，为了判断极大值或者极小值，我们会考虑泰勒级数中的第三项，

$$f(\vec{x}+\vec{\delta}) =f(\vec{x}) +\nabla^T f(\vec{x})\vec{\delta} +\frac{1}{2} \vec{\delta}^T \nabla^2f(\vec{x})\vec{\delta}$$ 很显然，如果Hessian矩阵正定，那么为局部极小点，反之为局部极大点。如果Hessian矩阵不定，则为鞍点。

3 拉格朗日乘数法

充分地将约束问题转化为无约束问题

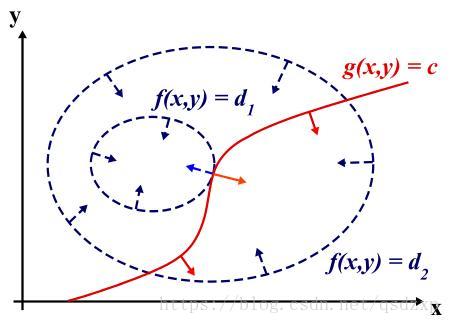
$$\begin{align} min \ \ &f(\vec{x}) \\ s.t. \ \ &g(\vec{x})=c \\ L(\vec{x})=f(&\vec{x}) +\lambda (g(\vec{x})-c) \end{align}$$ 下图以三维空间为例，虚线表示等高线。红色的曲线表示符合约束 $g(x,y)=c$的 $(x,y)$的集合。当 $f(x,y)$的某条等高线与红色曲线相切时， $f(x,y)$取得极值。其中， $L(\vec{x})$对 $\vec{x}$求偏导表示相切，对 $\lambda$求偏导表示约束。
注意：图中只是给出简单的单个极值点的情况，可能会有多个极值点。

3.2 KKT