1 范数（norm）

它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。一般我们用范数来衡量两个向量之间的距离，也就是相似度。

1.1常见的范数

0-范数
有多少个非零的数
1-范数（曼哈顿距离）

$| | x | |_{1} = | x_{1} | + | x_{2} | + \dots + | x_{n} |$ $||x||_1 =|x_1|+|x_2|+…+|x_n|$
2-范数 (欧几里得距离)

$| | x | |_{2} = \sqrt[2]{\sum_{1}^{n} x_{i}^{2}}$ $||x||_2= \sqrt[2]{\sum_1^n{x_i^2}}$
∞-范数

$| | x | |_{\infty} = m a x (| x_{1} |, | x_{2} |, \dots \dots | x_{n} |)$ $||x||_∞=max( |x_1|, |x_2|,……|x_n|)$

范式图例

2 向量和矩阵（Vector and Matrix）

既有大小，又有方向的量叫向量。一般来说在工程应用里，我们常用向量或者矩阵来表示一组数据，这样可以来表示数据的高维特性。而矩阵就是很多向量的集合。

2.1 向量的一些运算

加法
$a = [\begin{matrix} a_{1} \\ b_{1} \\ c_{1} \end{matrix}], b = [\begin{matrix} a_{2} \\ b_{2} \\ c_{2} \end{matrix}], a + b = [\begin{matrix} a_{1} + a_{2} \\ b_{1} + b_{2} \\ c_{1} + c_{2} \end{matrix}]$ $a= \begin{bmatrix} a_1\\ b_1 \\ c_1 \end{bmatrix} ,b= \begin{bmatrix} a_2\\ b_2 \\ c_2 \end{bmatrix} ,a+b=\begin{bmatrix} a_1+a_2\\ b_1+b_2 \\ c_1+c_2 \end{bmatrix}$
编程实现（python）

import numpy as np
a = np.array([-1, 2])
b = np.array([3, 1])
print a + b

向量和向量相乘
$a = [\begin{matrix} a_{1} \\ b_{1} \\ c_{1} \end{matrix}], b = [\begin{matrix} a_{2} \\ b_{2} \\ c_{2} \end{matrix}], a \cdot b = a_{1} * a_{2} + b_{1} * b_{2} + c_{1} * c_{2}$ $a= \begin{bmatrix} a_1\\ b_1 \\ c_1 \end{bmatrix} ,b= \begin{bmatrix} a_2\\ b_2 \\ c_2 \end{bmatrix},a·b=a_1*a_2+b_1*b_2+c_1*c_2$
编程实现（python）：

import numpy as np
a = np.array([3, 5, 2])
b = np.array([1, 4, 7])
print a.dot(b) 
print np.dot(a, b)

向量外积
$a = [\begin{matrix} a_{1} \\ b_{1} \\ c_{1} \end{matrix}], b = [\begin{matrix} a_{2} \\ b_{2} \\ c_{2} \end{matrix}], a \times b = [\begin{matrix} i, j, k \\ a_{1}, b_{1}, c_{1} \\ a_{2}, b_{2}, c_{2} \end{matrix}] = [\begin{matrix} b_{1} c_{2} - b_{2} c_{1} \\ a_{2} c_{1} - a_{1} c_{2} \\ a_{1} b_{2} - a_{2} b_{1} \end{matrix}]$ $a=\begin{bmatrix} a_1\\ b_1 \\ c_1 \end{bmatrix} ,b=\begin{bmatrix} a_2\\ b_2 \\ c_2 \end{bmatrix} ,a×b=\begin{bmatrix} i,j,k\\ a_1,b_1,c_1 \\ a_2,b_2,c_2 \end{bmatrix} =\begin{bmatrix} b_1c_2-b_2c_1\\ a_2c_1-a_1c_2\\ a_1b_2-a_2b_1 \end{bmatrix}$

import numpy as np
a = np.array([3, 5, 2])
b = np.array([1, 4, 7])
print np.cross(a, b)

矩阵向量积

\underset{m \times n}{A} \vec{x} = [\begin{matrix} a_{11} & a_{12} & \dots & a_{1 n} \\ a_{21} & a_{22} & \dots & a_{2 n} \\ \dots \\ a_{m 1} & a_{m 2} & \dots & a_{m n} \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ \dots \\ x_{n} \end{matrix}] = [\begin{matrix} a_{11} x_{1} + a_{12} x_{2} + \dots + a_{1 n} x_{n} \\ a_{21} x_{1} + a_{22} x_{2} + \dots + a_{2 n} x_{n} \\ \dots \\ a_{m 1} x_{1} + a_{m 2} x_{2} + \dots + a_{m n} x_{n} \end{matrix}]

$\underset{m\times n}{A}\vec{\mathbf{x}}=\begin{bmatrix}a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots \\ a_{m1} & a_{m2} & \ldots & a_{mn}\end{bmatrix}\begin{bmatrix}x_1 \\ x_2 \\ \ldots \\ x_n \end{bmatrix} = \begin{bmatrix}a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n \\ a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n \\ \ldots \\ a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n \\ \end{bmatrix}$
编程实现（python）：

import numpy as np 
a = np.matrix('4 3 1;1 2 5')
x = np.array([[5], [2], [7]])
print a*x

-向量的转置

\vec{V} = \underset{n \times 1}{\underset{⏟}{[\begin{matrix} v_{1} \\ v_{2} \\ \dots \\ v_{n} \end{matrix}]}}

$\vec{\mathbf{V}} = \underbrace{\begin{bmatrix}v_1 \\ v_2 \\ \ldots \\ v_n \end{bmatrix}}_{n\times 1}$
转置之后

{\vec{V}}^{T} = \underset{1 \times n}{\underset{⏟}{[\begin{matrix} v_{1} & v_{2} & \dots & v_{n} \end{matrix}]}}

$\vec{\mathbf{V}}^T = \underbrace{\begin{bmatrix}v_1 & v_2 & \ldots & v_n \end{bmatrix}}_{1 \times n}$
编程实现（python）

import numpy as np 
a = np.array([[2, 4]])
a.T

2.2 矩阵的特征向量和特征值（Eigenvector and Eigenvalue）

对一个方阵A，如果可以对A进行矩阵分解得到： $（v不是一个空向量）$

A v = λ v

$Av=\lambda v$

则 v 为 A 的 特 征 向 量 ， λ 为 A 的 特 征 值 ， 有 几 个 特 征 向 量 对 应 几 个 特 征 值 。

$则v为A的特征向量，\lambda 为A的特征值，有几个特征向量对应几个特征值。$

特征值分解

A = Q Σ Q^{- 1}

$A=Q\Sigma Q^{-1}$
其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角阵，每一个对角线上的元素就是一个特征值。首先，要明确的是，一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。

特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

编程实现（python）

import numpy as np      ##引入numpy模块
x=numpy.diag((1,2,3))   ##写入对角阵x
x                       ##输出对角阵x
array([[1,0,0],
[0,2,0],
[0,0,3]])
a,b=numpy.linalg.elg(x) ##特征值赋值给a，对应特征向量赋值给b 
a                       ##特征值 1 2 3
array([1.,2.,3.])
b                       ##特征向量
array([1.,0.,0.],
[0.,1.,0.],
[0.,0.,1.])

2.3 矩阵的迹（Trace Of Matrix）

t r (A) = \sum_{1}^{n} A_{i i}

$tr(A)=\sum_1^nA_{ii}$

import numpy as np      ##引入numpy模块
x=numpy.diag((1,2,3))   ##写入对角阵x
x                       ##输出对角阵x
x.trace()

2.4 奇异值分解（Singular Value Decomposition）

选自>https://blog.csdn.net/shenziheng1/article/details/52916278

特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有 $N$ 个学生，每个学生有 $M$ 科成绩，这样形成的一个 $N * M$ 的矩阵就不可能是方阵，我们怎样才能描述这样普通的矩阵呢的重要特征呢？奇异值分解可以用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法：

$A = U Σ V^{T}$ $A=U\Sigma V^T$
假设A是一个 $N * M$ 的矩阵，那么得到的 $U$ 是一个 $N * N$ 的方阵（里面的向量是正交的， $U$ 里面的向量称为左奇异向量）， $Σ$ 是一个 $N * M$ 的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值）， $V^T$ (V的转置)是一个 $N * N$ 的矩阵，里面的向量也是正交的， $V$ 里面的向量称为右奇异向量。

那么奇异值和特征值是怎么对应起来的呢？首先，我们将一个矩阵A的转置乘A，将会得到一个方阵，我们用这个方阵求特征值可以得到：

$(A^{T} A) v_{i} = λ v_{i}$ $(A^TA)v_i=\lambda v_i$
这里得到的v，就是我们上面的右奇异向量。此外我们还可以得到：
$σ_{i} = {\sqrt{λ}}_{i}$ $\sigma_i=\sqrt\lambda_i$
$u_{i} = \frac{1}{σ_{i}} A v_{i}$ $u_i={1\over\sigma_i}Av_i$
这里的σ就是上面说的奇异值，u就是上面说的左奇异向量。奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：
$A_{m \times n} \approx U_{m \times r} Σ_{r \times r} V_{r \times n}^{T}$ $A_{m\times n}\approx U_{m\times r}\Sigma_{r\times r} V^T_{r\times n}$
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。
编程实现（python）

import numpy as np
M = [[1,2,3],[4,5,6],[7,8,9]]
U,D,Vt = np.linalg.svd(M)

2.5 Jacobian Matrices and Hessian Matrices

2.5.1 Jacobian Matrices

在向量分析中, 雅可比矩阵是一阶偏导数以一定方式排列成的矩阵。
雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近. 因此, 雅可比矩阵类似于多元函数的导数。

J_{f} = [\begin{matrix} \frac{\partial f_{1}}{\partial x_{1}} & \dots & \frac{\partial f_{1}}{\partial x_{n}} \\ \dots & \dots & \dots \\ \frac{\partial f_{m}}{\partial x_{1}} & \dots & \frac{\partial f_{m}}{\partial x_{n}} \end{matrix}]

$J_f=\begin{bmatrix} {\partial f_1\over {\partial x_1}} &\ldots & {\partial f_1\over {\partial x_n}} \\ \dots &\ldots &\ldots\\ {\partial f_m\over {\partial x_1}}&\ldots & {\partial f_m\over {\partial x_n}} \end{bmatrix}$

[J_{f}]_{i j} = \frac{\partial f_{i}}{\partial x_{j}}

$[J_f]_{ij}= {\partial f_i\over {\partial x_j}}$

2.5.2 Hessian Matrices

海森矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵。

▽^{2} f = [\begin{matrix} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \dots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \dots & \dots & \dots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \dots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{matrix}]

$\bigtriangledown ^2f=\begin{bmatrix} {\partial^2 f\over {\partial x_1^2}} &\ldots & {\partial^2 f\over {\partial x_1 \partial x_n}} \\ \dots &\ldots &\ldots\\ {\partial^2 f\over {\partial x_n \partial x_1}}&\ldots & {\partial^2 f\over {\partial x_n^2}} \end{bmatrix}$

[▽^{2} f]_{i j} = \frac{\partial^{2} f}{\partial x_{i} \partial x_{j}}

$[\bigtriangledown ^2f]_{ij}= {\partial^2 f\over {\partial x_i \partial x_j}}$

3 张量（Tensor）

张量（Tensor）这个词来最早自于物理。比如我们常见的标量（Scalar）如质量、温度等，只有尺度（Magnitude）而没有方向（Direction）；向量（Vector）如重力、速度等，不仅有尺度大小还有一个方向。而张量则是在标量和向量的基础之上做的进一步推广。比如柯西应力张量（Cauchy’s stress tensor），是一个描述物体表面压力的物理量。如下图所示：
节选自>>https://www.wukong.com/question/6531498435785261325/

张量的提出是为了研究一些不依赖于坐标系的内在的几何性质和物理性质。相对论出现以后，张量这个概念被发扬光大了（相对论需要研究不同参考系下的同一物理系统的规律）。在现代数学上，张量定义为多重线性映射（multilinear map）。

TensorFlow中的Tensor或者说张量就是多维数组

1是一个0维张量/0维数组，又叫标量（scalar），形状为[]
[1, 2, 3]是一个1维张量/1维数组，又叫向量（vector），形状为[3].
[[1, 2, 3], [4, 5, 6]]是一个2维张量/2维数组，又叫矩阵（matrix），形状为[2, 3]
[[[1, 2, 3]], [[4, 5, 6]]]是一个3维张量/3维数组，有时候，张量特指3维以上的张量（低于3维的，如前所述，分别叫标量、向量、矩阵），形状为[2, 1, 3]

4 凹凸函数（Concave and Convex Function）

函数是凸的满足条件：

$f (t x + (1 - t) y) \leq t f (x) + (1 - t) f (y)$ $f(tx+(1-t)y)\le tf(x)+(1-t)f(y)$
$t \in [0, 1]$ $t\in [0,1]$

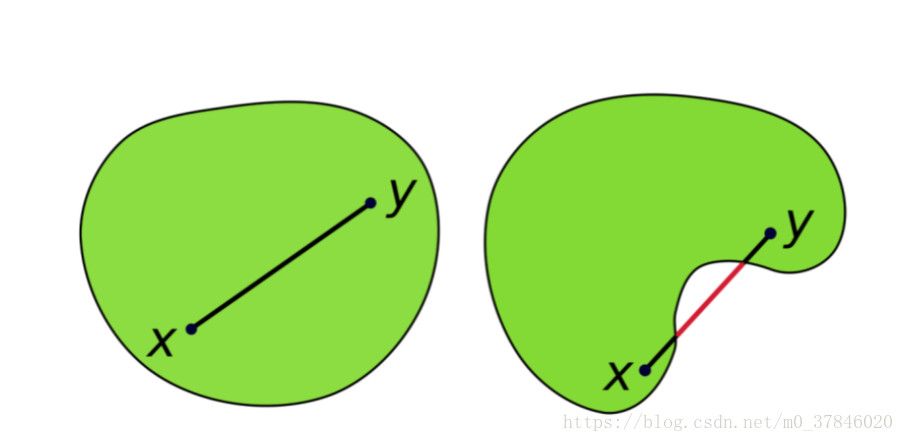
左边为凸函数，右边为凹函数。

机器学习的数学基础（壹）