Recommender Systems 推荐系统
Problem formulation
Example: Predicting movie ratings
电影评级预测的例子。
用户对电影进行评分:用0~5表示其对电影的喜好程度,?表示未看过该电影。
| Movie | Alice(1) | Bob(2) | Carol(3) | Dave(4) |
|---|---|---|---|---|
| Love at last | 5 | 5 | 0 | 0 |
| Romance forever | 5 | ? | ? | 0 |
| Cute puppies of love | ? | 4 | 0 | ? |
| Nonstop car chases | 0 | 0 | 5 | 4 |
| Swords vs. karate | 0 | 0 | 5 | ? |
通过上面的表格我们可以看出A和B喜欢看爱情相关的电影,不喜欢动作片;C和D刚好相反。我们就可据此推荐相关电影/未看过的电影。
定义符号表示如下:
- \(n_u\) = no. users
- \(n_m\) = no. movies
- \(r(i,j)\) = 1 if user \(j\) has rated movie \(i\)
- \(y^{(i,j)}\) = rating given by user \(j\) to movie \(i\) (defined only if \(r(i,j) = 1\))
此样例中,\(n_u = 4\), \(n_m = 5\), \(r(1,2) = 1\), \(y^{(1,2)} = 5\).
Content-based recommendations
基于内容的推荐系统。
Content-based recommender systems
对于上面出现的例子,我们查看数据并查看所有缺失的电影评级,并试图预测这些问号的值应该是多少。
在一个基于内容的推荐系统算法中,我们假设对于我们希望推荐的东西有一些数据,这些数据是有关这些东西的特征。假设每部电影都有两个特征,如\(x_1\)代表电影的浪漫程度,\(x_2\)代表电影的动作程度。则每部电影都有一个特征向量,如\(x^{(1)}\)是第一部电影的特征向量,为[0.9,0]。
| Movie | Alice(1) | Bob(2) | Carol(3) | Dave(4) | \(x_1\)(romance) | \(x_2\)(action) |
|---|---|---|---|---|---|---|
| Love at last | 5 | 5 | 0 | 0 | 0.9 | 0 |
| Romance forever | 5 | ? | ? | 0 | 1.0 | 0.01 |
| Cute puppies of love | ? | 4 | 0 | ? | 0.99 | 0 |
| Nonstop car chases | 0 | 0 | 5 | 4 | 0.1 | 1.0 |
| Swords vs. karate | 0 | 0 | 5 | ? | 1 | 0.9 |
For each user \(j\), learn a parameter \(\theta^{(j)} \in R^3\). Predict user \(j\) as rating movie \(i\) with \((\theta^{(j)})^Tx^{(i)}\) stars.
下面我们要基于这些特征来构建一个推荐系统算法。假设我们采用线性回归模型,我们可以针对每一个用户都训练一个线性回归模型,如\(\theta^{(1)}\)是第一个用户的模型的参数。于是,我们有:
- \(\theta^{(j)}\):用户\(j\)的参数向量,为\(n+1\)维。
- \(x^{(i)}\):电影\(i\)的特征向量。
- 对于用户\(j\)和电影\(i\),我们预测评分为\((\theta^{(j)})^Tx^{(i)}\)。
举个例子来进行说明:
已知\(x^{(3)} = \left[ \begin{matrix} 1 \\ 0.99 \\ 0 \end{matrix} \right]\),假如我们已知\(\theta^{(1)} = \left[ \begin{matrix} 0 \\ 5 \\ 0 \end{matrix} \right]\),则Alice对电影(3)的喜爱程度为\((\theta^{(1)})^Tx^{(3)} = 0.45\).
Optimization objective 最优化目标
针对用户\(j\),该线性回归模型的代价为预测误差的平方和,加上正则化项:
To learn \(\theta^{(j)}\) (parameter for user \(j\)):
\[ min_{\theta^{(j)}}\frac{1}{2}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)} - y^{(i,j)} \right)^2 + \frac{\lambda}{2}\sum^n_{k=1}(\theta_k^{(j)})^2 \]
其中\(i:r(i,j)=1\)表示我们只计算那些用户\(j\)评过分的电影。在一般的线性回归模型中,误差项和正则项应该都是乘以\(\frac{1}{2m}\),在这里我们将\(m\)去掉。并且我们不对方差项\(\theta_0\)进行正则化处理。
上面的代价函数只是针对一个用户的,为了学习所有用户,我们将所有用户的代价函数求和:
To learn \(\theta^{(1)},\theta^{(2)},\dots,\theta^{(n_u)}\):
\[ min_{\theta^{(1)},\dots,\theta^{(n_u)}}\frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)} - y^{(i,j)} \right)^2 + \frac{\lambda}{2}\sum_{j=1}^{n_u}\sum^n_{k=1}(\theta_k^{(j)})^2 \]
Optimization algorithm
Gradient descent update:
如果我们要用梯度下降法来求解最优解,我们计算代价函数的偏导数后得到梯度下降的更新公式为:
\[ \theta_k^{(j)} := \theta_k^{(j)} - \alpha\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)} - y^{(i,j)} \right)x_k^{(i)} \ \ (for\ \ k = 0) \\ \theta_k^{(j)} := \theta_k^{(j)} - \alpha\left(\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)} - y^{(i,j)} \right)x_k^{(i)} + \lambda x_k^{(j)}\right) \ \ (for\ \ k \ne 0) \]
Collaborative filtering
协同过滤算法
Problem motivation
在之前的基于内容的推荐系统中,对于每一部电影,我们都掌握了可用的特征,使用这些特征训练出了每一个用户的参数。相反地,如果我们拥有用户的参数,我们可以学习得出电影的特征。
Optimization algorithm 优化目标
Given \(\theta^{(1)},\dots.\theta^{(n_u)}\), to learn \(x^{(i)}\):
\[ min_{x^{(i)}} \frac{1}{2} \sum_{j:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum^n_{k=1}(x_k^{(i)})^2 \]
Given \(\theta^{(1)},\dots.\theta^{(n_u)}\), to learn \(x^{(1)},\dots,x^{(n_m)}\):
\[ min_{x^{(1)},\dots,x^{(n_m)}} \frac{1}{2}\sum^{n_m}_{i=1} \sum_{j:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum^{n_m}_{i=1}\sum^n_{k=1}(x_k^{(i)})^2 \]
Collaborative filtering
Given \(x^{(1)},\dots,x^{(n_m)}\) (and movie ratings), can estimate \(\theta^{(1)},\dots.\theta^{(n_u)}\).
Given \(\theta^{(1)},\dots.\theta^{(n_u)}\), can estimate \(x^{(1)},\dots,x^{(n_m)}\).
如果我们能知道\(\theta\)就能学习得到\(x\),如果我们知道\(x\)也会学习出\(\theta\)来。通过随机初始化参数,然后不停迭代,最终会收敛到一组合理的电影的特征和一组对不同用户参数的合理估计。
Collaborative filtering algorithm
Collaborative filtering optimization objective
将上面的两个优化目标合为一个。
Minimizing \(x^{(1)},\dots,x^{(n_m)}\) and \(\theta^{(1)},\dots.\theta^{(n_u)}\) simultaneously:
\(min_{x^{(1)},\dots,x^{(n_m)},\theta^{(1)},\dots.\theta^{(n_u)}}J(x^{(1)},\dots,x^{(n_m)},\theta^{(1)},\dots.\theta^{(n_u)})\),其中代价函数如下:
\[ J(x^{(1)},\dots,x^{(n_m)},\theta^{(1)},\dots.\theta^{(n_u)}) = \frac{1}{2}\sum_{(i:j):r(i,j) = 1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^n(x_k^{(i)})^2 + \frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^n(\theta_k^{(j)})^2 \]
Collaborative filtering algorithm
Initialize \(x^{(1)},\dots,x^{(n_m)},\theta^{(1)},\dots.\theta^{(n_u)}\) to small random values. 将\(x\)和\(\theta\)的值初始化为小的随机值
- Minimize \(J(x^{(1)},\dots,x^{(n_m)},\theta^{(1)},\dots.\theta^{(n_u)})\) using gradient descent (or an advanced optimization algorithm). E.g. for every \(j = 1,\dots,n_u,i=1,\dots,n_m\): 用梯度下降或者某些其他的高级最优化算法最小化代价函数
\[ x^{(i)}_k:= x^{(i)}_k - \alpha\left(\sum_{j:r(i,j) = 1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})\theta_k^{(j)} + \lambda x_k^{(i)} \right) \\ \theta^{(j)}_k:= \theta^{(j)}_k - \alpha\left(\sum_{i:r(i,j) = 1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})x_k^{(i)} + \lambda \theta_k^{(j)} \right) \] For a user with parameters \(\theta\) and a movie with (learned) features \(x\), predict a star rating of \(\theta^Tx\). 对于一个已知参数\(\theta\)的用户和一部已知特征\(x\)的电影,可以用训练完的算法为用户对电影的评分进行预测
Vectorization: Low rank matrix factorization
向量化:低秩矩阵分解
之前我们介绍了协同过滤算法,本节介绍该算法的向量化实现,以及说说有关该算法可以做的其他事情。如:
- 当给出一件产品时,你能否找到与之相关的其它产品。
- 一位用户最近看上一件产品,有没有其它相关的产品,你可以推荐给他。
要做的:实现一种选择的方法,写出协同过滤算法的预测情况。
Collaborative filtering
我们有关于五部电影的数据集,我将要做的是,将这些用户的电影评分,进行分组并存到一个矩阵中。

我们有五部电影,以及四位用户,那么这个矩阵\(Y\)就是一个5行4列的矩阵,它将这些电影的用户评分数据都存在矩阵里:
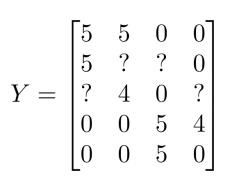
我们记:\(X = \left[ \begin{matrix} (x^{(1)})^T \\ (x^{(2)})^T \\ \dots \\ (x^{(n_m)})^T \end{matrix} \right]\),\(\Theta = \left[ \begin{matrix} (\theta^{(1)})^T \\ (\theta^{(2)})^T \\ \dots \\ (\theta^{(n_u)})^T \end{matrix} \right]\),则评分为:\(\left[ \begin{matrix} (\theta^{(1)})^T(x^{(1)}) & (\theta^{(2)})^T(x^{(1)}) & \dots & (\theta^{(n_u)})^T(x^{(1)}) \\ (\theta^{(1)})^T(x^{(2)}) & (\theta^{(2)})^T(x^{(2)}) & \dots & (\theta^{(n_u)})^T(x^{(2)}) \\ \vdots & \vdots & \vdots & \vdots \\ (\theta^{(1)})^T(x^{(n_m)}) & (\theta^{(2)})^T(x^{(n_m)}) & \dots & (\theta^{(n_u)})^T(x^{(n_m)}) \end{matrix} \right]\).
上述就是协同矩阵的向量化。
Finding related movies
For each product \(i\), we learn a feature vector \(x^{(i)} \in R^n\).
对每个产品\(i\),找出其特征向量\(x^{(i)}\)。
How to find movies \(j\) related to movie \(i\)?
如何找出与\(i\)相关的电影\(j\)?
5 most similar movies to movie \(i\): Find the 5 movies \(j\) with the smallest \(||x^{(i)} - x^{(j)}||\).
找出使两个商品特征比较相同的产品,即可以找出使得最小\(||x^{(i)} - x^{(j)}||\)的5个商品,则这5个商品就是和\(i\)最相似的5个商品,即可以作为相关产品推荐。
Implementational detail: Mean normalization
Users who have not rated any movies
假设有下面一组数据,即有一个用户未对电影进行任何评价。这时候如果我们使用之前的方法测Eve对每部电影的评分,则最小化图上的公式,因为对于任意i,Eve都没有评分过,因此公式中\(r(i, j)=1\)条件不满足,相关部分对于最小化Eve的数据没有作用,因此对于最小化Eve数据有作用的便只有\(min_{\theta^{(5)}}\frac{\lambda}{2}[(\theta_1^{(5)})^2 + (\theta_2^5)^2]\)部分。因两者都为\(0\),故\((\theta^{(5)})^T x^{(i)} = 0\),于是对Eve的预测评分都为\(0\)。
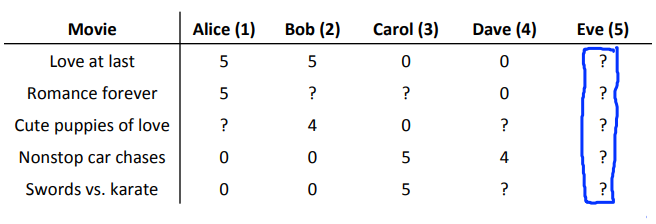
虽然结果是得出来了,但是这个结果我们没办法用来推荐,因为对所有的电影,其\(||x^{(i)} - x^{(j)}||\)都为\(0\)。
Mean Normalization
对于某一部电影,利用已经评过分的值(?不计算在内),计算出平均分,记为\(\mu\),于是归一化矩阵为原来的\(Y\)的每一个数减去这一行(这一部电影)对应的平均值,得到新的\(Y\),如下图右侧所示,利用这个新的\(Y\)矩阵学习\(\theta\)和\(x\)的值。则对于Eve,之前关于最小化的分析仍成立,即\(min_{\theta^{(5)}}\frac{\lambda}{2}[(\theta_1^{(5)})^2 + (\theta_2^5)^2]\)。
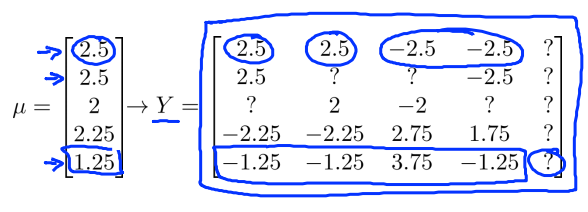
归一化之后的预测值公式为:\((\theta^{(5)})^Tx^{(i)} + \mu = \mu = \left[ \begin{matrix} 2.5 \\ 2.5 \\ 2 \\ 2.25 \\ 1.25 \end{matrix} \right]\)。
其实对于这个预测结果我们是可以接受的,因为我们不知道Eve的喜好,因此把她的评分预测为平均水平。
特殊情况:若出现有一部电影无评分的情况,则可以考虑使每列的均值为\(0\),即计算每列的均值,用\(Y\)减去对应列的均值得到新的\(Y\)矩阵。