机器学习（Machine Learning）- 吴恩达（Andrew Ng） 学习笔记（六）

Logistic Regression 逻辑回归

Classification

examples

Email: Spam/Not Spam? 电子邮件是否是垃圾邮件

Online Transactions: Fraudulent(Yes / No)? 网上交易是否是诈骗

Turmor: Malignant / Benign? 肿瘤是良性还是恶性

\(y \in \{0, 1\}\) 要预测的变量y能够取0和1两个值

0: "Negative Class" (e.g., benign tumor) 通常标记为0的类称为“负类”，如良性肿瘤

1: "Positive Class" (e.g., malignant tumor) 通常标记为1的类称为“正类”，如恶性肿瘤

用线性回归来解决分类问题

If \(h_\theta(x) \geq 0.5\), predict "y = 1"

If \(h_\theta(x) \leq 0.5\), predict "y = 0"

遇到的问题

分类问题预测的变量y只能是0或1，而\(h_\theta(x)\)有时会＞1或＜0。

--> 逻辑回归：\(0 \leq h_\theta(x) \leq 1\)（虽然名字中有“回归”，但实际上是个分类算法）

Hypothesis Representation 假设函数的表达式

在分类问题中，用什么样的函数来表示我们的假设。

Logistic Regression Model 逻辑回归模型

want \(0 \leq h_\theta(x) \leq 1\)

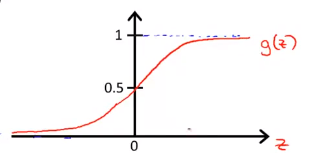
--> 另\(h_\theta(x) = g(\theta^Tx)\), 其中\(g(z) = \frac{1}{1 + e^{-z}}\), 称为逻辑函数(Sigmoid function/Logistic function)（这也是逻辑回归这个名字的由来）。

--> \(h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}}\)

Interpretation of Hypothesis Output 对假设输出结果的解释

1. \(h_\theta(x)\) = estimated probablity that \(y = 1\) on input \(x\).

2. Example: If \(x = \left[ \begin{matrix} x_0 \\ x_1 \end{matrix} \right] = \left[ \begin{matrix} 1 \\ tumorSize \end{matrix} \right]\),\(h_\theta(x) = 0.7\), tell patient that 70% chance of tumot being malignat. 对于一个特征值为x的患者，y = 1的概率是0.7，我将告诉我的病人肿瘤是恶性的可能性是70%。

3. \(h_\theta(x) = P(y = 1|x; \theta)\) "probability that y = 1, given x, parameterized by \(\theta\)" \(h_\theta\)就是给定x，y = 1的概率。上面例子中的x就是我的病人的特征x（肿瘤的大小）。

4. \(h_\theta(x) = P(y = 0|x; \theta) + h_\theta(x) = P(y = 1|x; \theta) = 1\)

   \(h_\theta(x) = P(y = 0|x; \theta) = 1 - h_\theta(x) = P(y = 1|x; \theta)\)

Decision boundary 决策边界

Logistic regression

\(h_\theta(x) = g(\theta^Tx)\), \(g(z) = \frac{1}{1 + e^{-z}}\).

Suppose predict "y = 1" if \(h_\theta(x) \geq 0.5\), predict "y = 0" if \(h_\theta(x) < 0.5\)

\(\because g(z) \geq 0.5\) when \(z \geq 0\)

\(\therefore h_\theta(x) = g(\theta^Tx) \geq 0\) when \(\theta^Tx \geq 0\).

\(\rightarrow\) \(\theta^Tx \geq 0\)时y = 1；\(\theta^Tx ＜ 0\)时，y = 0。

Decision Boundary

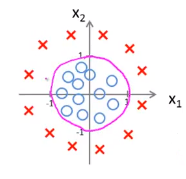
假设我们有下图所示的一个样例，它的假设函数为\(h_\theta(x) = g(\theta_0 + \theta_1x_1 + \theta_2x_2)\)。请你预测一下当\(\theta = \left[ \begin{matrix} -3 \\ 1 \\ 1 \end{matrix} \right]\)时，"y = 1"的概率。

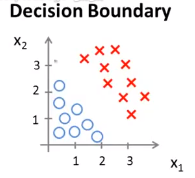
如果我们将假设函数可是话，我们将得到下图所示的一条分界线，这条分界线就叫做决策边界。

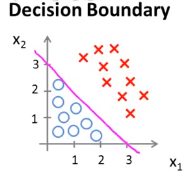
具体的说，这条直线上对应的点为\(h_\theta(x) = 0.5\)的点，它将平面划分为了两片区域——分别是假设函数预测y = 1的区域和假设函数预测y = 0的区域。

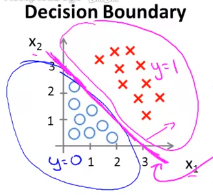
【注】决策边界是假设函数的一个属性，它包括参数\(\theta_0、\theta_1、\theta_2\)，与数据集无关。

Non-linear decision boundaries 非线性的决策边界

样例如下图，假设函数设为\(h_\theta(x) = g(\theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_1^2 + \theta_4x_2^2)\)，预测当\(\theta = \left[ \begin{matrix} -1 \\ 0 \\ 0 \\ 1 \\ 1 \end{matrix} \right]\)时，y = 1的概率。

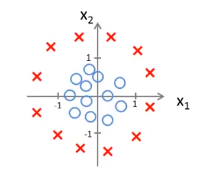
决策边界可视化：

Cost function

初寻代价函数

Linear regression: \(J(\theta) = \frac{1}{m}\sum_{i=1}^m\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2\)

另\(Cost(h_\theta(x), y) = \frac{1}{2}(h_\theta(x)-y)^2\)

由于\(h_\theta(x)\)函数是非线性的，故在这种情况下\(J(\theta)\)是非凸函数（下图左）。但我们使用梯度下降算法必须要求\(J(\theta)\)为凸函数（下图右）才可以。

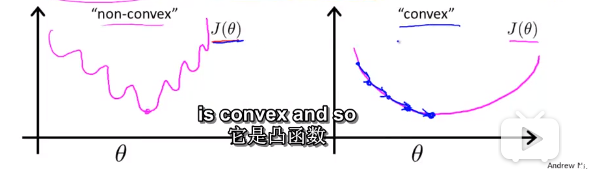
对此我们提出了新的代价函数。

Logistic regression cost function 逻辑回归的代价函数

\[ Cost(h_\theta(x), y) = \left\{ \begin{aligned} -log(h_\theta(x))\ \ \ \ \ \ if\ \ \ y = 1\\ -log(1 - h_\theta(x))\ \ \ \ \ \ if\ \ \ y = 0 \end{aligned} \right. \]

当y = 1时的详细解释：当假设函数的值和预测值都为1时，代价是0；但是当假设函数值为0预测值为1时，代价是\(\infty\)。y = 0时道理相同，图像刚好相反。

Simplified cost function and gradient descent

寻找一个简单点的方法来写代价函数替代现在的算法以及弄清楚如何运用梯度下降算法来拟合出逻辑回归的参数。

逻辑回归的代价函数的等价写法

\(Cost(h_\theta(x), y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x))\)

\(\rightarrow\) \(J(\theta) = \frac{1}{m}\sum_{i=1}^mCost(h_\theta(x), y) = -\frac{1}{m}\left[\sum_{i=1}^mylog(h_\theta(x)) + (1-y)log(1-h_\theta(x))\right]\)

这个式子是从统计学中的极大似然法中得来的，思路是基于如何为不同的模型有效地找出不同的参数。它还具有一个很好的性质——它是凸的。

接下来我们要做的就是想办法为训练集拟合出一个参数\(\theta\)，使得\(J(\theta)\)能取得最小值。而最小化\(J(\theta)\)的方法就是使用梯度下降法。

Gradient descent

1. 原始表达式：

   Want \(min_\theta J(\theta)\):

   Repeat {
   $\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta) $
   }

2. 带入上面化简后的式子：

   Want \(min_\theta J(\theta)\):
   Repeat {
   \(\theta_j := \theta_j - \alpha\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}\)
   }

3. 与线性回归的不同之处：假设函数的不同
   • 线性回归：\(h_\theta(x) = \theta^Tx\)
   • 逻辑回归：\(h_\theta(x) = \frac{1}{1+e^{-\theta^T x}}\)

Advanced optimization 高级优化

利用高级优化算法和概念我们可以将逻辑回归的速度大大提高，这也将使算法更适合大型的机器学习问题。

Optimization algorithm 优化算法

Given \(\theta\), we have code that can compute \(J(\theta)、\frac{\partial}{\partial \theta_j}J(\theta)\) (for \(j\) = 0, 1, …, n)

Optimization algorithms:

• Gradient descent
• Conjugate gradient 共轭梯度法
• BFGS
• L-BFGS

后三种算法的优点：

• No need to manually pick \(\alpha\)
• Often faster than gradient descent

后三种算法的缺点：

• More complex 太复杂了很难搞清楚其原理

调用函数时的建议

软件库有的函数，直接调用而不是自己写。

例子

\(\theta = \left[ \begin{matrix} \theta_1 \\ \theta_2 \end{matrix} \right]\)

\(J(\theta) = (\theta_1 - 5)^2 + (\theta_2 - 5)^2\)

\(\frac{\partial}{\partial\theta_1}J(\theta) = 2(\theta_1 - 5)\)

\(\frac{\partial}{\partial\theta_2}J(\theta) = 2(\theta_2 - 5)\)

编写函数：

function [jVal, gradient] = costFunction(theta)

jVal = (theta(1) - 5) ^2 + (theta(2) - 5)^2;
gradient = zeros(2, 1);
gradient(1) = 2 * (theta(1) - 5);
gradient(2) = 2 * (theta(2) - 5);

运行代码：

fminunc函数是内置的高级优化函数，它表示Octave里无约束最小化函数。具体用法如下：设置几个options，这些options变量作为一个数据结构可以存储你想要的options。GradObj和on是设置梯度目标参数为打开，这意味着你现在确实要给这个算法提供一个梯度，然后设置最大迭代次数，下面的例子中设置的次数为100。
@符号表示刚刚定义的costFunction函数的指针。它会自动选择学习速率\(\alpha\)，然后尝试使用这些高级的优化算法，就像加强版的梯度下降法，为你找到最佳的\(\theta\)值。

options = optimset('GradObj', 'on', 'MaxIter', '100');
initialTheta = zeros(2, 1)
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options)

functionVal是函数最后的值，exitFlag表示函数是否已经收敛。
欲要了解更过可通过help函数。

Multi-class classification: One-vs-all

Multiclass classification

多分类问题举例：

1. Email foldering/tagging: Work, Friends, Family, Hobby.

   假如你现在需要一个学习算法，可以自动地将邮件归类到不同文件夹里或者自动加上标签。

2. Medical diagrams: Not ill, Cold, Flu.

   如果一个病人因为鼻塞来找你诊断，他可能并没生病，或者感冒了，或者得了流感。

3. Weather: Sunny, Coludy, Rain, Snow.

   你正在做天气的机器学习分类问题，想要区分天气是晴天、多云、下雨天还是下雪天。

One-vs-all 一对多的方法

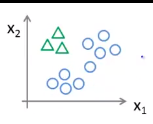
多分类问题图示：

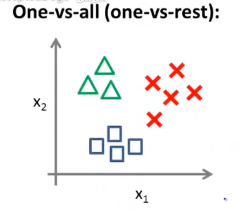
分类方法：制造新的“伪”训练集。
以三角形为例，将其定为正类，另外两种定为负类，我们创建一个新的训练集。接着拟合出一个合适的分类器，可记为\(h_\theta^{(1)}(x)\)。
接着将正方形定为正类，另外两种定为负类……便可得到\(h_\theta^{(2)}(x)\)、\(h_\theta^{(3)}(x)\)。

Train a logistic regression classifier \(h_\theta^{(i)}(x)\) for each class \(i\) to predict the probablity that \(y = i\). 对每一个可能的\(y = i\)都训练出一个逻辑回归分类器\(h_\theta^{(i)}(x)\)。

On a new input \(x\), to make a prediction, pick the class \(i\) that maximizes \(max_ih_\theta^{(i)}(x)\). 对于给出的\(x\)值，我们在我们得到的分类器里分别输入\(x\)值，然后选择一个让\(h\)最大的\(i\)。