分类问题通常分为两类:硬分类和软分类;
- 硬分类:只对样本的“硬性”类别感兴趣,即属于哪个类别;
- 软分类:即得到属于每个类别的概率;
这两者的界限往往很模糊,因为即使我们只关心硬类别,我们仍然使用软类别的模型。
文章目录
1.1.1 分类问题
常见的分类问题:
-
某个电子邮件是否属于垃圾邮件文件夹?
-
某个用户可能注册或不注册订阅服务?
-
某个图像描绘的是驴、狗、猫、还是鸡?
-
某人接下来最有可能看哪部电影?

我们从一个图像分类问题开始。 假设每次输入是一个 2×2 的灰度图像。 我们可以用一个标量表示每个像素值,每个图像对应四个特征 x1,x2,x3,x4 。 此外,假设每个图像属于类别“猫”,“鸡”和“狗”中的一个。
接下来,我们要选择如何表示标签。 我们有两个明显的选择:最直接的想法是选择 y∈{1,2,3} , 其中整数分别代表 {狗,猫,鸡} 。 这是在计算机上存储此类信息的有效方法。 如果类别间有一些自然顺序, 比如说我们试图预测 {婴儿,儿童,青少年,青年人,中年人,老年人} , 那么将这个问题转变为回归问题,并且保留这种格式是有意义的。
但是一般的分类问题并不与类别之间的自然顺序有关。 幸运的是,统计学家很早以前就发明了一种表示分类数据的简单方法:
独热编码(one-hot encoding)。独热编码是一个向量,它的分量和类别一样多。 类别对应的分量设置为1,其他所有分量设置为0。在我们的例子中,标签 y 将是一个三维向量, 其中 (1,0,0) 对应于“猫”、 (0,1,0) 对应于“鸡”、 (0,0,1) 对应于“狗”:
1.1.2 网络架构
为了估计所有可能类别的条件概率,我们需要一个有多个输出的模型,每个类别对应一个输出。 为了解决线性模型的分类问题,我们需要和输出一样多的仿射函数(affine function)。 每个输出对应于它自己的仿射函数。
在我们的例子中,由于我们有4个特征和3个可能的输出类别, 我们将需要12个标量来表示权重(带下标的 w ), 3个标量来表示偏置(带下标的 b )。
下面我们为每个输入计算三个未规范化的预测(logit): o1 、 o2 和 o3。
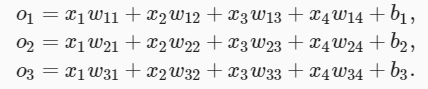
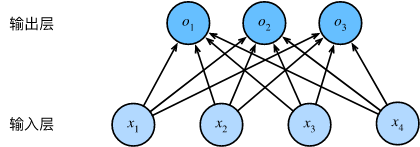
可以用神经网络图来描述这个计算过程。 与线性回归一样,softmax回归也是一个单层神经网络。 由于计算每个输出 o1 、 o2 和 o3 取决于 所有输入 x1 、 x2 、 x3 和 x4 , 所以softmax回归的输出层也是全连接层。
1.1.3 softmax运算
softmax函数将未规范化的预测变换为非负并且总和为1,同时要求模型保持可导。
我们首先对每个未规范化的预测求幂,这样可以确保输出非负。 为了确保最终输出的总和为1,我们再对每个求幂后的结果除以它们的总和。

尽管softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换决定。 因此,softmax回归是一个线性模型(linear model)。
1.1.4 小批量样本的矢量化
为了提高计算效率并且充分利用GPU,我们通常会针对小批量数据执行矢量计算。
假设读取了一个批量的样本 X , 其中特征维度(输入数量)为 d ,批量大小为 n 。假设在输出中有 q 个类别。
那么小批量特征为 X∈Rn×d , 权重为 W∈Rd×q , 偏置为 b∈R1×q 。。 softmax回归的矢量计算表达式为:
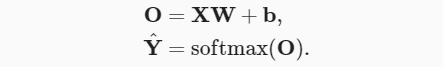
1.1.5 损失函数
使用最大似然估计,与在线性回归中的方法相同。
1.1.5.1 对数似然
softmax函数给出了一个向量 y^ , 我们可以将其视为“对给定任意输入 x 的每个类的条件概率”。
例如, y^1 = P(y=猫∣x) 。假设整个数据集 {X,Y} 具有 n 个样本,将估计值与实际值进行比较:
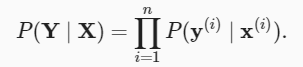
根据最大似然估计,我们最大化 P(Y∣X) ,相当于最小化负对数似然:
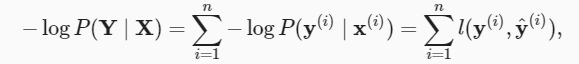
中,对于任何标签 y 和模型预测 y^ ,损失函数为:

这个损失函数 通常被称为交叉熵损失(cross-entropy loss)。
1.1.5.2 softmax及其导数
我们将1.1.3中的y^代入到损失函数中得:
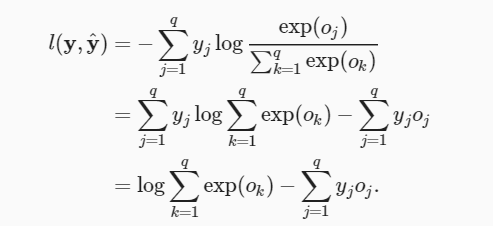
对oj 的导数,得到:
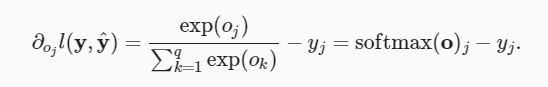
1.1.5.3 交叉熵损失
对于标签 y ,我们可以使用与以前相同的表示形式。 唯一的区别是,我们现在用一个概率向量表示,如 (0.1,0.2,0.7) , 而不是仅包含二元项的向量 (0,0,1) 。

损失 l 的定义如上,它是所有标签分布的预期损失值。 此损失称为交叉熵损失(cross-entropy loss),它是分类问题最常用的损失之一。
1.1.6 信息论基础
信息论(information theory)涉及编码、解码、发送以及尽可能简洁地处理信息或数据。
1.1.6.1 熵
信息论的核心思想是量化数据中的信息内容。 在信息论中,该数值被称为分布 P 的熵(entropy)。可以通过以下方程得到:
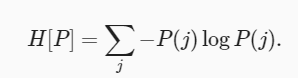
熵的本质是一个系统“内在的混乱程度”。
1.1.6.2 惊异
如果我们不能完全预测每一个事件,那么我们有时可能会感到“惊异”。 克劳德·香农决定用 log1/P(j)=−logP(j)来量化惊异(surprisal)。在观察一个事件 j ,并赋予它(主观)概率 P(j) 。 当我们赋予一个事件较低的概率时,我们的惊异会更大。
在 上文中定义的熵, 是当分配的概率真正匹配数据生成过程时的预期惊异(expected surprisal)。
1.1.6.3 重新审视交叉熵
交叉熵从 P 到 Q ,记为 H(P,Q) 。 你可以把交叉熵想象为“主观概率为 Q 的观察者在看到根据概率 P 生成的数据时的预期惊异”。当 P=Q 时,交叉熵达到最低。
简而言之,我们可以从两方面来考虑交叉熵分类目标:
- (i)最大化观测数据的似然;
- (ii)最小化传达标签所需的惊异。
1.1.7 模型预测和评估
在训练softmax回归模型后,给出任何样本特征,我们可以预测每个输出类别的概率。 通常我们使用预测概率最高的类别作为输出类别。 如果预测与实际类别(标签)一致,则预测是正确的。 在接下来的实验中,我们将使用精度(accuracy)来评估模型的性能。 精度等于正确预测数与预测总数之间的比率。
总结
- softmax运算获取一个向量并将其映射为概率。
- softmax回归适用于分类问题,它使用了softmax运算中输出类别的概率分布。
- 交叉熵是一个衡量两个概率分布之间差异的很好的度量。