用lm()拟合归回模型
回归分析作为一个统计学的核心,它其实是一个广义的概念,通指那些用一个或多个预测变量来(也称自变量或解释变量)来预测响应变量(也称因变量,校标变量或结果变量)
通常回归分析可以用来挑选与响应变量相关的解释变量,可以描述两者的关系,也可以生成一个等式,通过解释变量来预测响应变量。
回归分析的各种变体
1,简单线性–用一个量化的解释变量预测一个量化的响应变量(一元一次)
2,多项式–用一个量化的解释变量预测一个量化的响应的变量,模型的关系是n阶多项式(一元多次)
3,多层–用拥有等级结构的数据预测一个响应变量。也被称为分层模型,嵌套模型或混合模型
4,多元线性–用两个或多个量化的解释变量预测一个量化的响应的变量(多元一次)
5,多变量,用一个或多个解释变量预测多个响应变量
6,Logistic–用一个或多个解释变量预测一个类别型响应变量
7,泊松–用一个或多个解释变量预测一个代表频数的响应变量
8,Cox比例风险–用一个或多个解释变量预测一个事件发生的时间
9,时间序列–对误差项相关的时间序列数据建模
10,非线性–用一个或多个量化的解释变量预测一个量化的响应变量,不过模型是非线性的
11,非参数–用一个或多个量化的解释变量预测一个量化的响应变量,模型的形式源自数据形式,不事先设定
12,稳健–用一个或多个量化的解释变量预测一个量化的响应变量,能抵御强影响点的干扰
本章中我们的重点是普通最小二乘回归法,包括简单线性回归,多项式回归和多元线性回归。
为了能够恰当地解释OLS模型的系数,数据必须满足以下统计假设
1,正态性–对于固定的自变量值,因变量值成正态分布
2,独立性–Yi值之间相互独立
3,线性–因变量与自变量之间为线性相关
4,同方差性–因变量的方差不随自变量的水平不同而变化。也可称作不变方差
8.2.1用lm()拟合归回模型
在R中,拟合线性模型最基本的函数就是lm(),格式为
myfit <- lm(formula, data)
参数formula指要拟合的模型形式,表达式为YX1+X2+X3+…+Xk,左边为响应变量,右边为各个预测变量
参数data是一个数据框,包含了用于拟合模型的数据
结果对象存储在一个列表中,包含了模型的大量信息
R表达式中常用的符号
~, 分隔符号,左边为响应变量,右边为解释变量
+, 分隔预测变量
:, 表示预测变量的交互项。例如,要通过x, z及x与z的交互预测y,代码为y~x+z+x:z
*, 表示所有可能交互项的简洁方式。例如代码yx*w*z可展开为yx+w+z+x:z+x:w+z:w+x:z:w
^, 表示交互项达到某个次数。代码y(x+z+w)^2可展开为yx+z+w+x:z+x:w+z:w+x
., 表示包含除因变量外的所有变量,例如一个数据框包含变量x,y,z,w,代码y.可展开yx+z+w
-, 减号,表示从等式中移除某个变量。例如y(x+z+w)^2-x:w,可展开为yx+z+w+x:z+z:w+x
-1,删除截距项,例如y~x-1拟合y在x上的回归,并强制直线通过原点
Im(), 从算术的角度来解释括号中的元素,例如代码yx+I((z+w)^2)将展开为yx+h,h是一个由z和w的平方和创建的新变量
function, 可在在表达式中用的数学函数。例如log(y)~x+z+w
对拟合线性模型非常有用的其他函数
summary()–展示拟合模型的详细结果
coefficients()–列出拟合模型的模型参数(截距项和斜率)
confint()–提供模型参数的置信区间(默认95%)
fitted()–列出拟合模型的预测值
residuals–列出拟合模型的残差值
anova()–生成一个拟合模型的方差分析表,或者比较两个或更多拟合模型的方差分析表vcov()–列出模型参数的协方差矩阵
AIC()–输出赤池信息统计量
plot()–生成评价拟合模型的诊断图
predict()–用拟合模型对新的数据集预测响应变量值
当回归模型包括一个因变量和一个自变量时,我们称为简单线性回归。
当只有一个预测变量,但同时包含变量的幂时,我们称为多项式回归。
当有不止一个预测变量时,我们称为多元线性回归
简单线性回归例子
基础安装中的数据集women提供了15个年龄在30~39岁女性的身高和体重信息
通过 身高预测体重
通过lm()函数进行简单线性拟合
> fit <- lm(weight ~height, data=women)
> fit
Call:
lm(formula = weight ~ height, data = women)
Coefficients:
(Intercept) height
-87.52 3.45
使用summary()函数展示拟合模型的更详细结果
summary(fit)
Call:
lm(formula = weight ~ height, data = women)
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
height 3.45000 0.09114 37.85 1.09e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
从结果中可以看到回归系数为3.45显著不为0(p=1.1e-14),
R平方项0.991表示模型可以解释体重99.1%的方差。它也是实际和预测值之间的相关系数的平方。
残差标准误(1.53)则可以认为是模型用身高预测体重的平均误差
F统计量检验所有的预测变量预测响应变量是否都在某个几率水平上。由于简单回归只有一个预测变量,此处F检验等同于身高回归系数的t检验
> #使用coefficients()列出拟合模型的参数
> coefficients(fit)
(Intercept) height
-87.51667 3.45000
> #提供模型参数的置信区间(默认为0.95),从中可以看出参数的稳定性
> confint(fit)
2.5 % 97.5 %
(Intercept) -100.342655 -74.690679
height 3.253112 3.646888
> #输出数据框中女性体重的数据
> women$weight
[1] 115 117 120 123 126 129 132 135 139 142 146 150 154 159 164
> #列出拟合模型的预测值(会显示模型中提供的所有自变量通过模型得出的预测量,这样可以比较预测变量和因变量)
> fitted(fit)
1 2 3 4 5 6 7 8 9
112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.7333 140.1833
10 11 12 13 14 15
143.6333 147.0833 150.5333 153.9833 157.4333 160.8833
> #用拟合模型对新的数据集预测响应变量值
> predict(fit,newdata=data.frame(height=c(90,100)))
1 2
222.9833 257.4833
> #列出拟合模型的残差值
> residuals(fit)
1 2 3 4 5 6 7
2.41666667 0.96666667 0.51666667 0.06666667 -0.38333333 -0.83333333 -1.28333333
8 9 10 11 12 13 14
-1.73333333 -1.18333333 -1.63333333 -1.08333333 -0.53333333 0.01666667 1.56666667
15
3.11666667
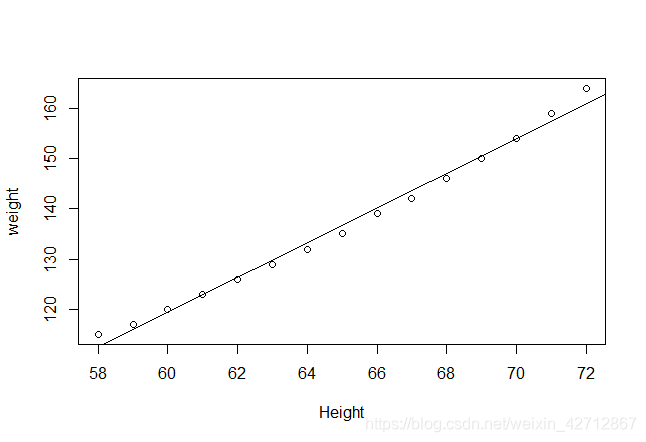
> plot(women$height,women$weight,xlab="Height",ylab="weight")
> #制作回归线(注意abline()函数只能制作线性的直线的回归线,非直线的回归线不能制作)
> abline(fit)
从图中可以看出你可以用一个弯曲的曲线来提高预测的精度,可以尝试使用多项式回归
8.2.3 多项式回归
从上个例子的图中可以看出可以添加一个二项次来提高回归的预测精度
例子
fit2 <- lm(weight~height + I(height^2),data=women)
> summary(fit2)
Call:
lm(formula = weight ~ height + I(height^2), data = women)
Residuals:
Min 1Q Median 3Q Max
-0.50941 -0.29611 -0.00941 0.28615 0.59706
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 261.87818 25.19677 10.393 2.36e-07 ***
height -7.34832 0.77769 -9.449 6.58e-07 ***
I(height^2) 0.08306 0.00598 13.891 9.32e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3841 on 12 degrees of freedom
Multiple R-squared: 0.9995, Adjusted R-squared: 0.9994
F-statistic: 1.139e+04 on 2 and 12 DF, p-value: < 2.2e-16
> #输出模型参数的置信区间
> confint(fit2)
2.5 % 97.5 %
(Intercept) 206.97913605 316.77723111
height -9.04276525 -5.65387341
I(height^2) 0.07003547 0.09609252
> #输出拟合模型的模型参数
> coefficients(fit2)
(Intercept) height I(height^2)
261.87818358 -7.34831933 0.08306399
> #输出拟合模型的预测值
> confint(fit2)
2.5 % 97.5 %
(Intercept) 206.97913605 316.77723111
height -9.04276525 -5.65387341
I(height^2) 0.07003547 0.09609252
> women$weight
[1] 115 117 120 123 126 129 132 135 139 142 146 150 154 159 164
> #输出拟合模型的预测值
> fitted(fit2)
1 2 3 4 5 6 7 8 9
115.1029 117.4731 120.0094 122.7118 125.5804 128.6151 131.8159 135.1828 138.7159
10 11 12 13 14 15
142.4151 146.2804 150.3118 154.5094 158.8731 163.4029
> #输出残差值
> residuals(fit2)
1 2 3 4 5 6
-0.102941176 -0.473109244 -0.009405301 0.288170653 0.419618617 0.384938591
7 8 9 10 11 12
0.184130575 -0.182805430 0.284130575 -0.415061409 -0.280381383 -0.311829347
13 14 15
-0.509405301 0.126890756 0.597058824
> #作图
> plot(women$height,women$weight,xlab="Height",ylab="Weight")
> #函数lines()其作用是在已有图上加线,命令为lines(x,y),其功能相当于plot(x,y,type="1")
> lines(women$height,fitted(fit2))
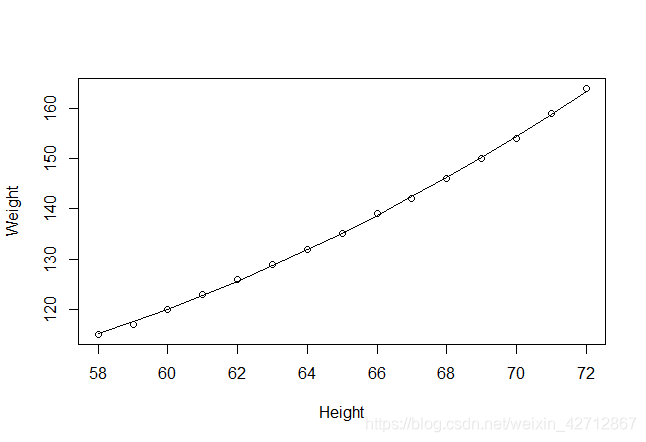
注意多项式等式仍可认为是线性回归模型,因为等式仍是预测变量的加权和形式
只有这样的形式才不是线性模型y=B0 + B1*e^(x/B2)
像这种y = log(x1) + sin(x2) 仍认为是线性的
注意使用比三次更高的项基本没有必要
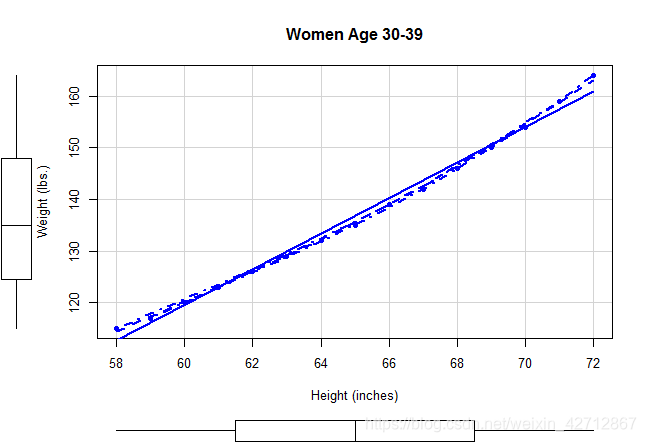
car包中的scatterplot()函数快速生成二元关系图
scatterplot()函数可以提供散点图,线性拟合曲线和平滑拟合曲线,还在响应边界展示了每个变量的箱线图。
spread=FALSE选项删除了残差正负均方根在平滑曲线上的展开和非对称信息,
smoother.args=list(lty=2)选项设置loess拟合曲线为虚线
library(car)
scatterplot(weight~height,data=women,spread=FALSE,smoother.args=list(lty=2),pch=19,
main="Women Age 30-39",
xlab="Height (inches)",
ylab="Weight (lbs.)")
8.2.4多元线性回归
当预测变量不止一个时,简单线性回归就变成了多元线性回归,
使用基础包中的state.x77数据集,探究一个州的犯罪率和其他因素的关系,包括人口,文盲率,平均收入和结霜天数
states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
names(states)
[1] "Murder" "Population" "Illiteracy" "Income" "Frost"
在多元回归分析中,第一步需要检查一下变量间的相关性。
cor()函数提供了二变量之间的相关系数,car包中的scatterplotMatrix()函数则会生成散点图矩阵
示例
states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
> names(states)
[1] "Murder" "Population" "Illiteracy" "Income" "Frost"
> cor(states)
Murder Population Illiteracy Income Frost
Murder 1.0000000 0.3436428 0.7029752 -0.2300776 -0.5388834
Population 0.3436428 1.0000000 0.1076224 0.2082276 -0.3321525
Illiteracy 0.7029752 0.1076224 1.0000000 -0.4370752 -0.6719470
Income -0.2300776 0.2082276 -0.4370752 1.0000000 0.2262822
Frost -0.5388834 -0.3321525 -0.6719470 0.2262822 1.0000000
> library(car)
> scatterplotMatrix(states,spread=FALSE,smoother.args=list(lty=2),main="Scatter Plot Matrix")

scatterplotMatrix()函数默认在非对角区域绘制变量间的散点图,并添加平滑和线性拟合曲线。
对角线区域绘制每个变量的密度图和轴须图
从图中可以看到,谋杀率是双峰的曲线,每个预测变量都一定程度上出现了偏斜,谋杀率随着人口和文盲率的增加而增加,随着收入水平和结霜天数增加而下降。
使用lm()函数拟合多元线性回归模型
states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
> fit <- lm(Murder~.,data=states)
> summary(fit)
Call:
lm(formula = Murder ~ ., data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
> residuals(fit)
Alabama Alaska Arizona Arkansas California
4.11179210 3.27433977 -1.68700264 0.26668056 -0.57424792
Colorado Connecticut Delaware Florida Georgia
1.68594493 -3.81042204 0.73768277 1.91178879 2.97838044
Hawaii Idaho Illinois Indiana Iowa
-3.41984294 1.05927673 2.42954793 1.41893921 -2.02545720
Kansas Kentucky Louisiana Maine Maryland
-0.09731294 1.68494109 -0.72117551 -2.00277259 2.21479548
Massachusetts Michigan Minnesota Mississippi Missouri
-4.15834611 3.72023253 -2.69149081 0.57035176 3.34806321
Montana Nebraska Nevada New Hampshire New Jersey
0.74271628 -1.53684814 7.62104160 -1.39312273 -2.63613735
New Mexico New York North Carolina North Dakota Ohio
-1.20643853 -0.54123176 0.89516295 -3.72716517 0.08408941
Oklahoma Oregon Pennsylvania Rhode Island South Carolina
-0.30323290 -0.35693643 -2.29005973 -4.79596633 -0.06492602
South Dakota Tennessee Texas Utah Vermont
-2.12674691 1.50235895 -1.17607560 0.17189817 1.32479323
Virginia Washington West Virginia Wisconsin Wyoming
0.99906692 -0.54828949 -1.02808130 -2.53545933 2.70090366
> confint(fit)
2.5 % 97.5 %
(Intercept) -6.552191e+00 9.0213182149
Population 4.136397e-05 0.0004059867
Illiteracy 2.381799e+00 5.9038743192
Income -1.312611e-03 0.0014414600
Frost -1.966781e-02 0.0208304170
> fitted(fit)
Alabama Alaska Arizona Arkansas California
10.988208 8.025660 9.487003 9.833319 10.874248
Colorado Connecticut Delaware Florida Georgia
5.114055 6.910422 5.462317 8.788211 10.921620
Hawaii Idaho Illinois Indiana Iowa
9.619843 4.240723 7.870452 5.681061 4.325457
Kansas Kentucky Louisiana Maine Maryland
4.597313 8.915059 13.921176 4.702773 6.285205
Massachusetts Michigan Minnesota Mississippi Missouri
7.458346 7.379767 4.991491 11.929648 5.951937
Montana Nebraska Nevada New Hampshire New Jersey
4.257284 4.436848 3.878958 4.693123 7.836137
New Mexico New York North Carolina North Dakota Ohio
10.906439 11.441232 10.204837 5.127165 7.315911
Oklahoma Oregon Pennsylvania Rhode Island South Carolina
6.703233 4.556936 8.390060 7.195966 11.664926
South Dakota Tennessee Texas Utah Vermont
3.826747 9.497641 13.376076 4.328102 4.175207
Virginia Washington West Virginia Wisconsin Wyoming
8.500933 4.848289 7.728081 5.535459 4.199096
当预测变量不止一个时,回归系数的含义为:一个预测变量增加一个单位,其他预测变量保持不变时,因变量将要增加的数量。
8.2.5有交互项的多元线性回归
若两个预测变量的交互项显著,说明响应变量与其中一个预测变量的关系依赖于另一个预测变量的水平
fit <- lm(mpg ~ hp +wt + hp:wt,data=mtcars)
> summary(fit)
Call:
lm(formula = mpg ~ hp + wt + hp:wt, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.0632 -1.6491 -0.7362 1.4211 4.5513
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.80842 3.60516 13.816 5.01e-14 ***
hp -0.12010 0.02470 -4.863 4.04e-05 ***
wt -8.21662 1.26971 -6.471 5.20e-07 ***
hp:wt 0.02785 0.00742 3.753 0.000811 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.153 on 28 degrees of freedom
Multiple R-squared: 0.8848, Adjusted R-squared: 0.8724
F-statistic: 71.66 on 3 and 28 DF, p-value: 2.981e-13
>
通过effects包中的effect()函数,可以展示交互项结果
effect函数的格式为
plot(effect(term,mod,xlevels),multiline=TRUE)
根据lm()函数生成的二元一次方程,给定因变量中的一个因变量几个固定值得到不同的一元一次方程,然后作图
library(effects)
plot(effect("hp:wt",fit,,list(wt=c(2.2,3.2,4.2))),multiline=TRUE)
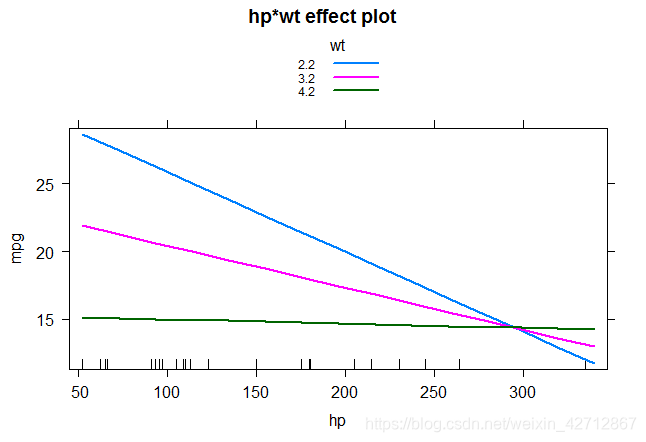
从图中可以看到hp和mpg的斜率随着wt的改变而改变,说明对于mpg来说hp和wt存在交互,如果不存在交互,当wt不同时hp和mpg的关系只会改变截距而不会改变斜率。
