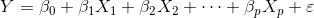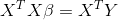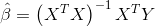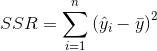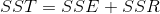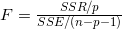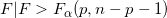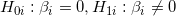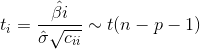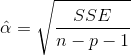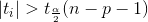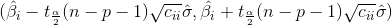多元线性回归分析（R语言）

▼多元线性回归分析▼

一、多元线性回归模型

设变量Y与X1，X2，……，Xp之间有线性关系

$Y = \beta _{0} + \beta _{1} X_{1}+ \beta _{2} X_{2}+ \cdots +\beta _{p} X_{p} + \varepsilon$

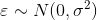
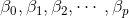
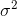
其中 $\varepsilon \sim N(0,\sigma ^{^{2}})$ ， $\beta _{0},\beta _{1},\beta _{2},\cdots ,\beta _{p}$ 和 $\sigma ^{2}$ 是未知参数，p≥2，称上公式为多元线性回归模型。

二、参数估计

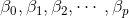
我们根据多元线性回归模型，认为误差 $\varepsilon$ 应是比较小的，然后对 $\beta _{0},\beta _{1},\beta _{2},\cdots ,\beta _{p}$ 求偏导并令其等于0，可以得到正规方程：

$X^{^{T}}X\beta = X^{T}Y$

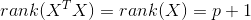
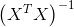
因为 $rank(X^{T}X) = rank(X) = p+1$ ，故 $\left ( X^{T} X\right )^{-1}$ 存在，解正规方程，可以得到β的最小二乘估计：

$\hat{\beta }=\left ( X^{T}X \right )^{-1}X^{T}Y$

三、回归方程的显著性检验

给出定义：回归方程的显著性检验等价于检验回归系数是否全为零，即检验：

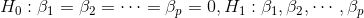
$H_{0}:\beta _{1}=\beta _{2}=\cdots =\beta _{p}=0,H_{1}:\beta _{1},\beta _{2},\cdots ,\beta _{p}$ 不全为零

下面给出必要的公式：

残差平方和SSE：

$SSE=\sum_{i=1}^{n}\left ( y_{i} -\hat{y}\right )^{2}$

回归平方和SSR：

$SSR=\sum_{i=1}^{n}\left (\hat{} y_{i} -\bar{y}\right )^{2}$

总的离差平方和：

SST=SSE+SSR

统计量F：

$F=\frac{SSR/p}{SSE/(n-p-1)}$

对于给定的显著性水平α，检验的拒绝域：

$F|F>F_{\alpha }(p,n-p-1)$

四、回归系数的显著性检验

回归方程显著，并不意味着每个自变量对因变量的影响都显著，通常会进行回归系数的检验，假设检验为：

$H_{0i}:\beta _{i}=0, H_{1i}:\beta _{i}\neq 0$

给出t值检验法公式：

$t_{i}=\frac{\hat{\beta i}}{\hat{\sigma }\sqrt{c_{ii}}}\sim t(n-p-1)$

其中

$\hat{\alpha }=\sqrt{\frac{SSE}{n-p-1}}$

对于给定的显著性水平α，检验的拒绝域：

$|t_{i}|>t_{\frac{\alpha }{2}}(n-p-1)$

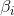
另外，还可以确定 $\beta _{i}$ 的置信度为1-α的置信区间：

$(\hat{\beta _{i}}-t_{\frac{\alpha }{2}}(n-p-1)\sqrt{c_{ii}}\hat{\sigma},\hat{\beta _{i}}+t_{\frac{\alpha }{2}}(n-p-1)\sqrt{c_{ii}}\hat{\sigma})$

五、例题实战

题目： 文件“T3house.txt”中给出了美国某住宅区的20个家庭房价相关数据。

数据：T3house.txt

15.31 57.3 74.8
15.20 63.8 74.0
16.25 65.4 72.9
14.33 57.0 70.0
14.57 63.8 74.9
17.33 63.2 76.0
14.48 60.2 72.0
14.91 57.7 73.5
15.25 56.4 74.5
13.89 55.6 73.5
15.18 62.6 71.5
14.44 63.4 71.0
14.87 60.2 78.9
18.63 67.2 86.5
15.20 57.1 68.0
25.76 89.6 102.0
19.05 68.6 84.0
15.37 60.1 69.0
18.06 66.3 88.0
16.35 65.8 76.0

a.将矩阵第一列记为变量z1=总居住面积，第二列记为变量z2=评估价值，第三列记为Y=售价。

library(foreign)
data <-read.table("T3house.txt")
data1<-as.matrix(data[1:20,1:3],dimnames="cc")
colnames(data1) <- c("z1","z2","Y");data1

b.将a中的各个变量生成数据框，做关于Y和z1,z2的回归，显示计算结果。

data2<-data.frame(data1);data2

#使用内置函数
#lm.1<-lm(Y~z1+z2,data=data2)
#summary(lm.1)

#自编程序
z0<-c(rep(1,20))
data3<-data.frame(z0,data2)
attach(data3)
A<-as.matrix(data3)
X<-A[1:20,1:3]
Y<-A[1:20,4]
Y<-as.vector(Y)
b<-solve(t(X)%*%X)%*%t(X)%*%Y;b
#结果
#z0 30.96656634
#z1  2.63439962
#z2  0.04518386
#故回归方程为Y=30.6656634+2.63439962 z1 + 0.04518386 z2

c.根据b中的结果分别给出β1和β2的置信系数为90%的置信区间。

data3<-data.frame(z0,data2);data3
n<-nrow(data3);
p<-ncol(data3);
p<-p-1
C<-solve(t(X)%*%X)
A<-as.matrix(data3)
X<-A[1:20,1:3]
lm.1<-lm(Y~z1+z2,data=data3)
SSE=deviance(lm.1)
shita<-sqrt(SSE/(n-p-1))
t1<-b[2]/(shita*sqrt(C[1,1]));t1
t2<-b[3]/(shita*sqrt(C[2,2]));t2
b1<-c(b[2]-1.7247*shita*sqrt(C[1,1]),b[2]+1.7247*shita*sqrt(C[1,1]));b1
b2<-c(b[3]-1.7247*shita*sqrt(C[2,2]),b[3]+1.7247*shita*sqrt(C[2,2]));b2
#结果
#-11.37843  16.64723
#-1.351438  1.441806

d.假设某房间总居住面积为15，评估价值为55，试给出该房屋售价的点估计、预测区间和估计区间（置信系数95%）。

y0<-b[1]+15*b[2]+55*b[3];y0
#点估计72.96767

newdata<-data.frame(z1=15,z2=55)
lmpred<-predict(lm.1,newdata,interval="prediction",level=0.95)
lmpred

e.计算20个房屋价格的拟合值，并做残差对拟合值的残差图。

resid<-residuals(lm.1)
pre<-predict(lm.1);pre #等价于y,拟合值

#方法二
y=x
for(i in 1:20)
{
  y[i]=b[1]+X[i,2]*b[2]+X[i,3]*b[3]
}
y; #拟合值
plot(pre,resid)

f.计算回归系数β的最小二乘估计，误差方差σ2的估计，残差向量，残差平方和，回归平方和，方程显著性检验F统计量，复相关系数，修正的复相关系数。将上述8个量写入一个列表并显示出结果。

#第一个量
b;
#第二个量
shita2<-SSE/(n-p-1);shita2
#第三个量
e<-Y-X%*%b;e
#第四个量
y1<-mean(Y)
sse<-0
for(i in 1:20)
{
   y[i]=b[1]+X[i,2]*b[2]+X[i,3]*b[3]
}
for(j in 1:20)
{
   sse<-sse+(Y[j]-y[j])**2
}
sse;
#第五个量
ssr<-0;
y0<-mean(Y)
for(k in 1:20)
{
  ssr<-ssr+(y[k]-y0)**2
}
ssr;
#第六个量
F<-(ssr/p)/(sse/(n-p-1));F
#第七个量
R<-ssr/(sse+ssr);R
#第八个量
R2<-sqrt(1-(sse/(n-p-1))/((sse+ssr)/(n-1)));R2
#列表
list.data <- list(b, shita2, e, sse, ssr,F,R,R2);list.data

相关资料：数据分析与R软件第二版（李素兰著）每章例题代码和数据，下载地址：https://download.csdn.net/download/lph188/10802159