1. 决策树
决策树是一种分类算法,它像是一个倒着的树,遵循if—then原则来对样本进行分类,如下图:
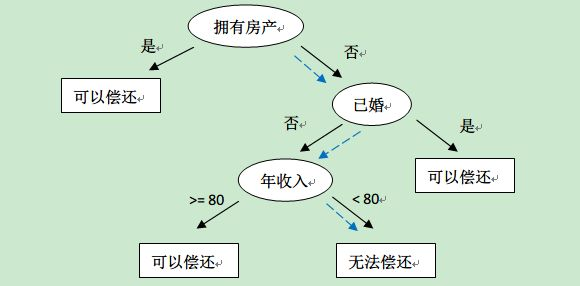
这是一个简单的决策树模型,它通过样本数据的特征来一点一点判断,最终将样本归到正确的分类中。最上面的"拥有房产"这个节点称为根节点,中间诸如"已婚"、"年收入"等节点称为内部节点,内部节点就是表示一个特征或属性的取值。“可以偿还”、"无法偿还"等节点称为叶节点,叶节点对应着类别。
2. 信息熵
有些地方把信息熵叫做信息量,其实也能大致这样理解。信息量就是你知道一件事以后能得到的信息的多少,说白了是一种度量单位,然而得到信息的多少跟事件发生的概率有关系。最常举的例子,若有人告诉你,“太阳从东方升起从西方落下”,那你得到的信息量就为0,因为这件事发生的概率为1,就是一定会发生,所以在别人告诉你的那一刻,你就没有获得信息量。若别人告诉你,世界杯国足出线了,那么你获得的信息量就是巨大的,因为这件事发生的概率太低了(皮一下很开心)。从这里我们就得到了一条重要的性质或者可以叫信息熵的一条必要条件:信息熵随着事件发生的概率的增大而减小。
若别人告诉你国足出线了,这件事的概率记做P(x),信息熵为X。同时又告诉你,今天上课点名了,这件事的概率记做P(y),信息熵为Y。你知道了两件事,你所得到的信息量一定是X+Y,然而这两件事情是独立的(不要说老师知道你看球故意点名),他们同时发生的概率P(x,y)=P(x)P(y)。这便得到了信息熵的第三个性质:两件独立的事情发生时,概率是乘积,信息熵是累加。
如果要用一个公式来表示信息熵,从第三条性质我们很容易想到它一定与log有关系,然而log是个递增函数,我们需要个递减的,那么log前面一定需要加一个负号。还要不为负数,那么一定是概率作为log的自变量,因为概率最大为1。综上所述,信息熵的公式就浮出水面了。
从随机变量角度来看,随机变量X的可能取值有
,对于每个可能的取值,其概率
,因此随机变量X的熵为:
为什么用2作为底数?其实这里用e作为底数也行,这里的log只是为了实现第一条性质和第三条性质,它的底数是没关系的,所以根据传统取2。
从离散样本空间角度来看,对于样本集合D来说,假设样本有K个类别,
表示类别k的样本个数,
表示样本总数,则对于样本集合D来说熵为:
信息熵计算代码实现:
from math import log
def getShannonEnt(dataSet):
dataNum=len(dataSet)
labelCounts={}
for data in dataSet:
label=data[-1] #获取标签
if label not in labelCounts.keys():
labelCounts[label]=0
labelCounts[label]+=1
ShannonEnt=0.0
for key in labelCounts:
#计算概率=频数/总数
pro=float(labelCounts[key])/dataNum
# print(f'pro[{key}]={pro}')
#累加香农熵
ShannonEnt -=pro*log(pro,2)
return ShannonEnt
dataSet=[[1,1],[2,1],[3,0],[4,1],[5,0]]
print(f'ShannonEnt={getShannonEnt(dataSet)}')
dataSet=[[1,1],[2,1],[3,0],[4,1],[5,0],[6,1],[7,1],[8,0],[9,1],[10,2]]
print(f'ShannonEnt={getShannonEnt(dataSet)}')
ShannonEnt=0.9709505944546686
ShannonEnt=1.295461844238322
以weka中的天气数据为例(weather.norminal.arff),数据集如下图所示:
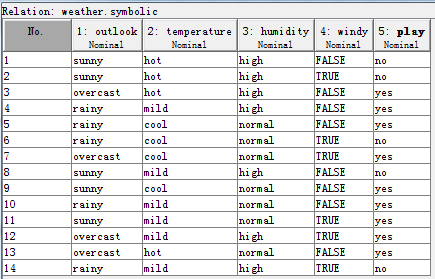
令D为天气数据集,共14个样本,每个样本有5个属性。类别标签属性play有两个值
。C1=yes在D中出现的概率为
,C2=no出现的概率为
。因此D的熵为:
dataSet=[[1,0],[2,0],[3,1],[4,1],[5,1],[6,0],[7,1],[8,0],[9,1],[10,1],[11,1],[12,1],[13,1],[14,0]]
print(f'ShannonEnt={getShannonEnt(dataSet)}')
ShannonEnt=0.9402859586706309
3. 特征选择
特征选择指选择有较强分类能力的特征。**而分类能力通过信息增益或者信息增益比来刻画。**选择特征的标准是找出局部最优的特征作为判断进行切分,取决于切分后节点数据集合中类别的有序程度(纯度),划分后的分区数据越纯,切分规则越合适。衡量节点数据集合的纯度有:熵、基尼系数和方差。熵和基尼系数是针对分类的,方差是针对回归的。
4. 信息增益(ID3算法)
ID3名字中的ID是Iterative Dichotomiser(迭代二分器)的简称。
信息增益(gain)是熵与条件熵的差。前面是训练集D的熵,表示训练机D的不确定程度。后面是训练集D在特征A给定的情况下不确定程度。那么二者的差值就可以理解为由于给定了特征A,训练集D的不确定性降低了多少。显然,这个值越大说明这个特征对提纯的贡献越多。
根据信息增益的特征选择方法为:对数据集D的每个特征计算其信息增益,然后排序,选择最大的最为最先划分的特征。根据此特征划分之后可以形成几波子集(取决于此特征的取值多少),然后在这些子集上再分别计算信息增益并选择最大的进行划分,这样不断循环下去,直到所有特征都被划分完。
计算每个属性划分数据集D所得的信息增益:
以上面天气数据中的属性windy为例,取值为{FASLE,TRUE},将D划分为2个子集{
(8个),
(6个)}。
对于
,play=yes 有6个样本,play=no 有2个样本,则:
对于
,play=yes 有3个样本,play=no 有3个样本,则:
D1=[[1,0],[2,1],[3,1],[4,1],[5,0],[6,1],[7,1],[8,1]]
print(f'H(D1)={getShannonEnt(D1)}')
D2=[[1,0],[2,0],[3,1],[4,1],[5,1],[6,0]]
print(f'H(D2)={getShannonEnt(D2)}')
H(D1)=0.8112781244591328
H(D2)=1.0
利用属性windy划分D后的条件熵为:
则按属性windy划分数据集D所得的信息增益值为:
同理,得到S对其他所有属性的信息增益,如下所示:
,
,
如果只用ID3算法,则将信息增益取值最大的那个属性作为分裂节点,因此以outlook属性作为决策树的根节点。接下来根决策节点的三个不同取值的分支,递归计算信息增益,求子树,最后得到的决策树。
ID3算法的缺点:
1、无法处理连续值特征,比如来一个西瓜的密度作为特征,密度的数值是连续的,它就无法处理。
2、对取值较多的特征有偏向。若数据集中最左侧的编号No.也作为一个特征的话,那么他被首先选上是必然的,因为总共14条数据它就有14个取值,意思是用它来划分将会产生14个分支,这14个分支每个分支仅仅包含一个样本,纯度自然非常非常高。当然这是一个比较极端的例子,但也反映了ID3算法对取值较多的特征有偏向。
3、没有考虑缺失值的处理。
4、没有考虑过拟合。
5. 信息增益比(C4.5算法)
信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的 C4.5 决策树算法(Quinlan 1993)不直接使用信息增益,而是使用"增益率" (gain ratio) 来选择最优划分属性。信息增益比定义为:
其中 ,表示将当前特征A作为随机变量(取值为特征A的各个特征值)求得的经验熵。
以outlook属性为例,取值为overcast的样本有4条,取值为rain的样本有5条,取值为sunny的样本有5条:
那么,
同理,计算其他属性的信息增益比:
使用C4.5算法则将信息增益率取值最大的那个属性作为分裂节点,因此以outlook属性作为决策树的根节点。接下来根决策节点的三个不同取值的分支,递归计算信息增益比,求子树。最后得到的决策树如下图:
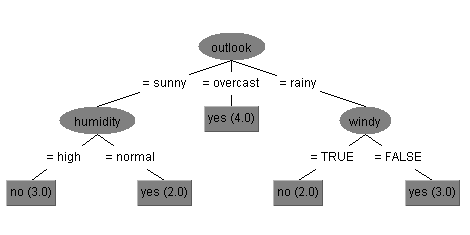
基本的决策树的生成算法中,典型的有ID3生成算法和C4.5生成算法,它们生成树的过程大致相似,ID3是采用的信息增益作为特征选择的度量,而C4.5则采用信息增益比。
虽然C4.5算法改进了ID3算法的一些缺点,但其自身仍有缺点:
1、容易过拟合。(决策树过拟合的解决方法一般是剪枝)
2、C4.5生成的是多叉树结构,运行效率较低。(二叉树效率高)
3、C4.5中的大量的对数计算影响效率。
4、C4.5算法只能处理分类问题。
6. CART 决策树
CART全称为Classification and Regression Tree(分类与回归树),这是一种著名的决策树学习算法,分类和回归任务都可用。基本原理还是与之前的两个算法相同,不同的仍然是选择特征的依据。
CART决策树[Breiman et al., 1984] 使用"基尼指数" (Gini index) 来选择划分属性。数据集的纯度可用基尼值来度量:
基尼指数反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,基尼指数越小,数据集的纯度越高。
那么特征A的基尼指数定义为:
7. 决策树停止生成条件
决策树不会无限制的生长,总会有停止分裂的时候,最极端情况为节点分裂到只剩一个数据点时自动停止分裂。为降低决策树的复杂度和提高预测精度,会适当提前终止节点的分裂(先剪枝)。决策树停止分裂的一般性条件为:
- 最小节点数
当节点数小于一个指定数时,不再继续分裂。因为数据量较少时,再做分裂容易强化噪声数据的作用。其次,降低树生长的复杂性,提前结束分裂一定程度上有利于降低过拟合的影响。 - 熵或基尼指数小于阀值
熵和基尼指数的大小表示数据的复杂程度,当熵或者基尼值过小时,表示数据的纯度比较大,如果熵或者基尼值小于一定程度数,节点停止分裂。 - 决策树的深度达到指定上限。
- 所有特征已经使用完毕。
8. 总结
三个决策树算法总结对比:
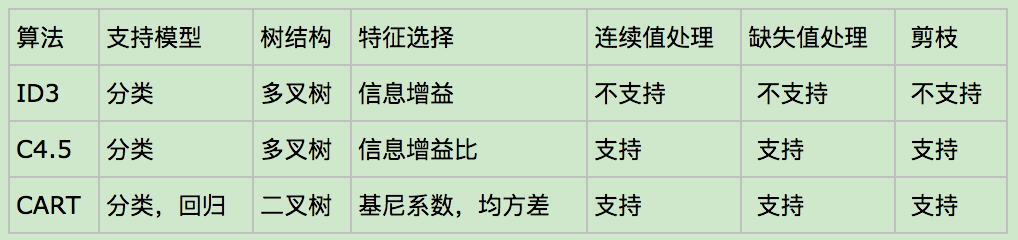
参考资料:
《决策树》
《机器学习笔记 16_决策树》
《机器学习-周志华》
《机器学习实战-李锐》
本文主要参考前两篇文章,摘选片段根据自己的理解进行重新排版整合,并对公式符号进行统一描述。
