场景
之前有说过k近邻算法,k近邻算法是根据寻找最相似特征的邻居来解决分类问题。k近邻算法存在的问题是:不支持自我纠错,无法呈现数据格式,且吃性能。k近邻算法的决策过程并不可视化。对缺失数据的样本处理很不友好,而且当处理具有许多特征的高维数据时,K-NN的性能可能会下降。
熵
在了解决策树之前,有必要了解一个熵的概念,这是高数必学的一个东西。
熵(Entropy)的定义
熵是信息论中的一个核心概念,最初由克劳德·香农提出。它是用来量化信息中的不确定性或混乱度的度量。在信息论中,熵可以理解为传输的信息量或系统的无序程度。
举例
抛硬币,硬币有正有反,理论上抛到正面和抛到负面的概率是一样大,我跑了三次硬币,分别是
| 次数 | 结果 |
|---|---|
| 1 | 正 |
| 2 | 反 |
| 3 | 正 |
问:我第四抛硬币的结果是什么?
这不扯淡吗?我怎么会知道?这种情况下的熵是最大的。
拿小球,我一个袋子里有一百个球,其中一个黑球,九十九个白球,问:你会拿到什么球?
我可以直接预测:白球。
结论是:不确定性较小,熵也相应较低。不确定性越高,熵就越高。
数学上,对于一个离散随机变量 X,其熵 H(X) 可以通过以下公式定义:
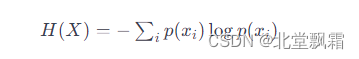
有了公式我们可以计算一下抛一枚硬币的熵值是多少?
from math import log2
# 抛硬币是一个典型的二分类问题,正面和反面出现的概率相等,都是0.5
prob_head = 0.5 # 正面的概率
prob_tail = 0.5 # 反面的概率
# 根据熵的公式计算熵
entropy = - (prob_head * log2(prob_head) + prob_tail * log2(prob_tail))
entropy
结果是 1
熵和决策树
案例
假设我们有以下简单的数据集,它包含了一些关于天气条件的观察结果,以及人们是否选择出门郊游的决定:
| 天气 | 温度 | 风速 | 出门郊游 |
|---|---|---|---|
| 晴朗 | 热 | 高 | 否 |
| 雨天 | 凉 | 低 | 是 |
| 阴天 | 温暖 | 高 | 是 |
| 晴朗 | 凉 | 低 | 否 |
| 晴朗 | 温暖 | 高 | 是 |
| 雨天 | 热 | 高 | 否 |
| 阴天 | 凉 | 低 | 是 |
步骤1:计算数据集的熵
首先,我们计算整个数据集的熵。熵是衡量数据集不确定性的度量,它基于最终决定(出门郊游)的分布。
在这个数据集中,有4个“是”和3个“否”。因此,数据集的熵将基于这两个类别的分布来计算。
# 计算熵
def calcShannonEnt(dataSet):
# 统计实例总数
numEntries = len(dataSet)
# 字典标签,统计标签出现的次数
labelCounts = {
}
for data in dataSet:
# 每个实例的最后一个元素是标签元素
currentLabel = data[-1]
if currentLabel not in labelCounts:
labelCounts[currentLabel] = 0
# 为当前类别标签的计数加一
labelCounts[currentLabel] += 1
# 设置初始熵
shannonEnt = 0.0 # 初始化熵为0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries # 计算每个类别标签的出现概率
shannonEnt -= prob * log(prob, 2) # 使用香农熵公式计算并累加熵
return shannonEnt # 返回计算得到的熵
步骤2:特征分割
接下来,我们尝试不同的特征来分割数据集,并计算每种分割的熵。
例如,以“天气”为分割特征:
当天气为“晴朗”时,我们有3个样本,其中有1个“是”和2个“否”。
当天气为“雨天”时,有2个样本,都是“否”。
当天气为“阴天”时,有2个样本,都是“是”。
除了天气,我们还有其他的特征,遍历所有的特征,并且得到所有特征的熵累加
for i in range(numFeatures): # 遍历所有特征
featList = [example[i] for example in dataSet] # 提取当前特征列的所有值
uniqueVals = set(featList) # 获取当前特征的唯一值集合
newEntropy = 0.0 # 初始化新熵
for value in uniqueVals: # 遍历当前特征的每个唯一值
subDataSet = splitDataSet(dataSet, i, value) # 根据当前特征和值分割数据集
prob = len(subDataSet) / float(len(dataSet)) # 计算子数据集的比例
newEntropy += prob * calcShannonEnt(subDataSet) # 计算新熵,并累加
步骤3:计算信息增益
什么是信息增益?
信息增益衡量的是在知道某个特征的信息之后,数据集熵的减少量,即该特征给我们带来多少信息。

H(D) 是数据集的熵,H(D∣A) 是在知道特征 A 的信息之后数据集 D 的条件熵。
这是数据集当前的熵,初始化最佳信息增益, 初始化最佳特征的索引,初始化新熵
baseEntropy = calcShannonEnt(dataSet) # 计算数据集当前的熵
bestInfoGain = 0.0 # 初始化最佳信息增益
bestFeature = -1 # 初始化最佳特征的索引
newEntropy = 0.0 # 初始化新熵
目前我们有三种天气,分别是晴朗,雨天,阴天。
那么,晴朗占总数据的多少?subDataSet是总数据集中晴朗的数据明细,那么算出晴朗的熵,然后到了雨天,阴天同理,将他们的熵累加起来。
for value in uniqueVals: # 遍历当前特征的每个唯一值
subDataSet = splitDataSet(dataSet, i, value) # 根据当前特征和值分割数据集
prob = len(subDataSet) / float(len(dataSet)) # 计算子数据集的比例
newEntropy += prob * calcShannonEnt(subDataSet) # 计算新熵,并累加
构建决策树
决策树
决策树是一种流行的机器学习算法,用于分类和回归任务。它模拟了人类决策过程的方式,通过一系列的问题来推导出结论。
基本原理:
节点:决策树由节点组成,包括决策节点和叶节点。决策节点表示一个属性或特征,叶节点代表决策的结果。
分割:从根节点开始,根据数据集的特征对数据进行分割,每个分割创建子节点。
信息增益:选择分割的特征基于信息增益(或其他类似指标,如Gini不纯度)。目标是选择能最有效提高决策纯度的特征。
递归:重复这个过程,为每个子节点继续创建更深层次的分割,直到满足停止条件(如达到预定深度,或子节点纯度足够高)。
和熵关联起来
我们之前得到了每一个特征的熵,也得到了他们的信息增益。根据前面的例子(自行计算)我们选择具有最大信息增益的特征来分割数据集。这意味着该特征在减少预测是否去郊游的不确定性方面最有效。在我们的例子中,假设“天气”特征带来了最大的信息增益,那么它将成为决策树的第一个决策点。基于“天气”特征构建决策树的顶部。然后,针对“晴朗”、“雨天”和“阴天”这三个子集重复上述过程,选择下一个最佳分割特征,直到所有子集都足够“纯净”或达到树的最大深度。通过这个过程,熵和信息增益帮助我们识别哪些特征对于预测结果最重要,从而可以构建一个有效的决策树模型。每次分割旨在创建更“纯净”的子集,最终构建出能够准确预测新样本类别的决策树。
总结
我们通过信息增益构建决策树,决策树类似于if else条件流程,我们可以使用python的绘图工具画出来。决策树的范例,如下,我们通过决策树就可以直接得到预测结果。
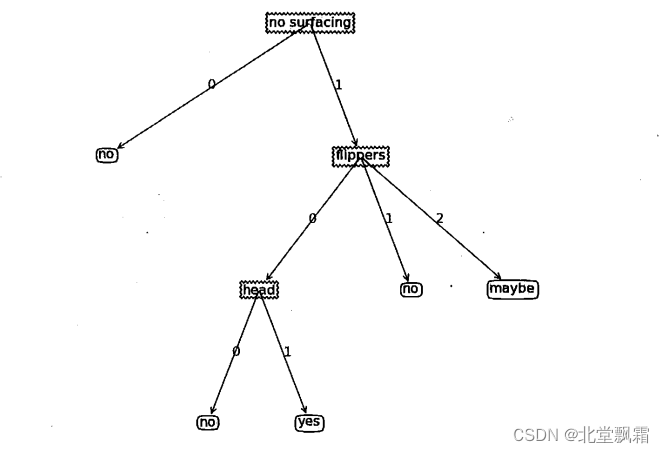
结束
决策树虽然是一个强大且易于理解的机器学习工具,但它们也有一些缺点和局限性:
过拟合问题:决策树非常容易过拟合,尤其是当树变得非常深或复杂时。过拟合意味着树对训练数据过于精确地建模,从而捕捉到了噪声和异常值,这会降低其在新数据上的预测性能。
不稳定性:决策树可能对数据中的小变化非常敏感。即使是非常小的数据变动,也可能导致生成完全不同的树。
处理非线性问题的能力有限:决策树可能不擅长处理数据间的复杂关系或非线性问题。例如,如果类别边界是圆形的,单一的决策树可能很难处理这样的情况。
信息增益偏好:在选择分割的特征时,决策树倾向于选择拥有更多水平(levels)的特征,这并不总是最佳选择。
结果不一定最优:决策树算法(如ID3、C4.5、CART)通常使用启发式方法来构建树,这意味着结果可能并不是全局最优的。
类别不平衡问题:如果数据集中的类别分布极不平衡,决策树可能会偏向于多数类,从而影响模型的性能。
由于这些原因,决策树通常与其他技术(如剪枝、集成方法等)结合使用,以提高其性能和鲁棒性。例如,随机森林和梯度提升树就是使用决策树构建的集成学习算法,它们通常能提供比单个决策树更好的性能和泛化能力。