开始，从4个盒子里以等概率（0.25,0.25,0.25,0.25）随机抽取1个盒子，从这个盒子里随机抽出1个球，记录颜色后，放回。
然后，从当前盒子随机转移到下一个盒子，规则是：如果当前盒子是盒子1，那么下一盒子一定是2；如果当前盒子是2或3，那么分别以概率0.4和0.6转移到左边或右边的盒子；如果当前盒子是4，那么各以0.5的概率停留在盒子4或转移到盒子3。

转移概率	1盒子	2盒子	3盒子	4盒子
初始概率，也就是第一次拿球的概率	0.25	0.25	0.25	0.25
如果上一次是1盒子，这次取球概率	0	1	0	0
如果上一次是2盒子，这次取球概率	0.4	0	0.6	0
如果上一次是3盒子，这次取球概率	0	0.4	0	0.6
如果上一次是4盒子，这次取球概率	0	0	0.5	0.5

确定转移的盒子后，再从这个盒子里随机抽出1个球，记录其颜色，放回。
如此下去，重复5次，得到一个球的颜色的观测序列：O = {红，红，白，白，红}

分析如下：

在这个过程中，观测者只能观测到球的颜色的序列，观测不到球是从哪个盒子取出的，即观测不到盒子的序列（状态序列）。

这个例子中，有两个随机序列，一个是盒子的序列（状态序列），一个是球的颜色的观测序列（观测序列）。前者是隐藏的，后者是可观测的。根据所给条件，可以明确状态集合、观测集合、序列长度、模型的三要素（初始概率，状态转移概率，观测概率）。

盒子对应状态，状态的集合是：Q = {盒子1，盒子2，盒子3，盒子4}，长度：N = 4

球的颜色对应观测。观测的集合是：V = {红，白}，长度：M = 2

状态序列（隐藏的抽盒子序列）和观测序列（得到的球的序列）长度 T = 5,

初始化概率分布为：

状态转移概率分布为：

观测概率分布为：

解释 B：

B = {从1盒子拿到红、白球的概率；从2盒子拿到红、白球的概率；从3盒子拿到红、白球的概率；从4盒子拿到红、白球的概率}

1.2 隐马尔可夫模型的定义：

1.2.1 定义

记住上面例子的关键术语，下面概念+公式，就更容易理解。

隐马尔可夫模型是关于时序的概率模型，

也就是说：这个模型是根据时间的顺序（即事情发生的先后顺序），推导的下一个事情发生的概率的模型。

描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测从而产生观测随机序列的过程。

直白地说：有一个过程，隐藏的随机发生，不可知，这个过程叫“隐藏的马尔可夫链”，是一个观测不到的状态，且这个状态是随机的，是根据时间的顺序发生。接着，有好多隐藏的状态发生，然后产生了一个可观测到的结果，就是我们看到的红白球序列。

（上面黑体是定义，只是为了解释，被我拆成了两行）

状态序列：隐藏的马尔可夫链随机生成的状态的序列（跟事件发生了几次有关）。

观测序列：每个状态生成一个观测，而由此产生的观测的随机序列（跟事件发生了几次有关）。

序列的每一个位置又可以看做是一个时刻。

隐马尔可夫模型由三个东西确定：初始概率分布π + 状态转移概率分布 A+ 观测概率分布B。隐马尔可夫模型的形式定义如下：

设 Q 是所有可能的状态的集合（对应盒子种类集合），N 是可能的状态数，
设 V 是所有可能的观测的集合（对应球种类集合），M 是可能的观测数，
设 I 是长度为 T 的状态序列（隐藏的从哪个盒子取的序列），T 是长度，
设 O 是对应的观测序列（可看到的红白球的序列），
A是状态转移概率矩阵：，从一种状态出发，到另一种状态。共有N种状态，所以是N*N。

其中，

是在时刻 t 处于状态 qi （处于某个盒子）的条件下，在时刻 t+1 转移到状态 qj （处于某个盒子）的概率。

B是观测矩阵概率：

其中，

是在时刻 t 处于状态 qj （某盒子）的条件下，生成观测 vk （红球还是白球）的概率。

π 是初始状态概率向量：

其中，

是时刻 t = 1 处于状态 qi 的概率（第一次，选择某个盒子的概率，如例子中，第一次每个盒子被选中的概率都是0.25）。

A B π 是隐马尔可夫模型的三要素：

状态转移概率矩阵 A 与初始状态概率向量 π 确定了隐藏的马尔可夫链，生成不可观测的状态序列。观测概率 B 确定了如何从状态生成观测（从每个盒子单独抽取红白球的概率），与状态序列综合确定了如何产生观测序列。

1.2.2 隐藏的马尔可夫模型的两个基本假设

（1）齐次马尔可夫性假设。即假设隐藏的马尔可夫链在任意时刻 t 的状态只依赖于其前一时刻的状态， 与其他时刻的状态及观测无关，也与 t 无关：

（2）观测独立性假设。即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关（也就是本次选取的红白球，跟之前从哪个盒子选取哪个球没有什么关系，只跟这次是从哪个盒子取的，有关。）：

隐藏的马尔可夫模型可以用于标注，这时状态对应着标记。标注问题是给定观测的序列，预测其对应的标记序列。可以假设标注问题的数量是由隐马尔可夫模型生成的。这样我们可以利用隐藏的马尔可夫模型的学习与预测算法进行标注。

1.2.3 公式证明两个基本假设

用公式证明两个假设：

状态序列，观测序列，长度为T。也就是抽取的盒子的序列为 I, 看到的球的序列为 O，共发生了 T 次。

根据贝叶斯公式可知：P(A|B) = P(A) * P(B|A) / P(B),

对应盒子和球，就是：P(I|O) = P(I) * P(O|I) / P(O)，

$\large P(I|O) = P(i_{1}, i_{2}, ..., i_{t} | o_{1}, o_{2}, ..., o_{t})$

$\large = P(i_{1}, i_{2}, ..., i_{t}) *P( o_{1}, o_{2}, ..., o_{t} | i_{1}, i_{2}, ..., i_{t}) / P(o_{1}, o_{2}, ..., o_{t})$

其中，

$\large P(i_{1}, i_{2}, ..., i_{t})$

$\large =P(i_{1})*P( i_{2}, i_{3}, ..., i_{t} | i_{1})$

$\large =P(i_{1})*P(i_{2} | i_{1})*P(i_{3}, ..., i_{t} | i_{1}, i_{2})$

$\large =P(i_{1})*P(i_{2}|i_{1})*P(i_{3}|i_{1}, i_{2}) * P(i_{4}, ..., i_{t} | i_{1}, i_{2}, i_{3})$

$\large \cdot \cdot \cdot =P(i_{1})\prod_{2}^{t}P(i_{i}|i_{1}, i_{2}, ..., i_{t-1})$

$\large =P(i_{1})\prod_{2}^{t}P(i_{t} | i_{t-1})$ (1)

(1) 结果，根据齐次性假设，t 时刻的状态，只依赖于前一次的状态，上面式子的最后一个连乘公式

$\large P( o_{1}, o_{2}, ..., o_{t} | i_{1}, i_{2}, ..., i_{t})$

$\large =P(o_{1})*P(o_{2}, o_{3}, ..., o_{t} | i_{1}, i_{2}, ..., i_{t}, o_{1})$

$\large =P(o_{1})*P(o_{2})*P(o_{3}, ..., o_{t} | i_{1}, i_{2}, ..., i_{t}, o_{1}, o_{2})$

$\large =\prod_{i=1}^{t}P(o_{i} | i_{i})$ （2）

（2）结果，根据独立性假设，o 球的状态，只取决于 i 盒子的状态。

由于分母的观测概率是已发生事件，所以设为1。P(I|O)可以写成下面的形式：

$\large P(I|O) = P(i_{1}, i_{2}, ..., i_{t} | o_{1}, o_{2}, ..., o_{t})$

$\large \propto P(i_{1})\prod_{2}^{t}P(i_{t} | i_{t-1}) * \prod_{i=1}^{t}P(o_{i} | i_{i})$

1.3 观测序列的生成过程

根据隐马尔可夫模型定义，可以将一个长度为 T 的观测序列的生成过程描述如下：

输入：隐马尔可夫模型，观测序列长度为 T

输出：观测序列

按照初始化状态分布 π 产生状态 $i_{1}$ ；
令 t = 1；
按照状态 $\large i_{t}$ 的观测概率分布 $\large b_{i_t{}}(k)$ 生成 $\large o_{t}$ ;
按照状态 $\large i_{t}$ 的转移概率分布 { $\LARGE { a_{i_{t}i_{t+1}} }$ } 产生
令 t = t + 1；如果 t < T,转步骤 3，否则，终止。

1.4 隐马尔可夫模型的3个基本问题

隐马尔可夫模型有3个基本问题：

（1）概率计算问题。给定模型，和观测序列，计算在模型 λ 下观测序列 O 出现的概率 P(O|λ )。

（2）学习问题。一直观测序列，估计模型参数，使得在该模型下观测序列概率 P(O|λ) 最大。即用极大似然估计的方法估计参数。

（3）预测问题，也称为解码问题。已知模型和观测序列，求对给定观测序列（即已知球的颜色）条件概率 P(I|O) 最大的状态序列。即给定观测序列，求最优可能的对应的状态序列。直白的说：已知球的颜色的序列，求依次选取盒子的序列。

2 概率计算算法

下面介绍计算观测概率 P(O|λ ) 的前向（forward）与后向（backward）算法。

2.1 直接计算算法

概念可行，但计算上不可行。

给定模型和观测序列，计算观测序列 O 出现的概率 P(O|λ ) 。也就是说：三要素知道了，且看到了取出球个序列。计算一下在前面已经发生的情况下，下一次 O 出现的概率。

最直接的方法是按照概率公式直接计算。通过列举所有可能的长度为 T 的状态序列，求各个状态序列 I 与观测序列的联合概率 P(O，I |λ ) ，然后对所有可能的状态序列求和，得到 P(O|λ )。

状态序列 的概率是：

解释：初始概率乘以每一个盒子的转移概率？？

对固定的状态序列，观测序列的概率是：

解释：求某次取出球为O球的概率，就需要把前面每个球的概率，都求出来，然后再继续成上本次球出现的概率。（理解为T叉树，应该是对的，就是每一个结点，下面有T个枝子，都需要计算。）？？

O 和 I 同时出现的联合概率为：

然后，对所有可能的状态序列 I 求和，得到观测序列 O 的概率 P(O|λ ) ，即

使用上面 P(O|λ ) 的公式，计算量很大，是O(TN^T)阶的，所有不可行。下面介绍有效算法，前向-后向算法。

2.2 前向算法

前向概率定义：给定隐马尔可夫模型 λ ，定义到时刻 t ，部分观测序列为 $\large o_{1},o_{2},o_{3}...o_{t},$ 且状态为 $\large q_{j}$ 的概率为前向概率，记作：

可以递推地求得前向概率 $\large \alpha _{t}(i)$ 及观测序列概率 P(O|λ )。

观测序列概率的前向算法推导过程：

输入：隐马尔可夫模型 λ ，观测序列 O；
输出：观测序列概率 P(O|λ ) 。

（1）初值

解释：选中某盒子的概率，乘以，从这个盒子中取出某颜色球的概率。（i 理解为第几个盒子）

（2）递推，对 t = 1,2,......, T-1,

解释：t 时刻之前的都确定好了，然后 t 时刻乘以当前的转移概率，再乘以从某盒子(第 i 个盒子)抽球的概率。

（3）终止

前向算法，步骤（1）初始化前向概率，是初始时刻的状态 $\large i_{1} = q_{i}$ 和观测 $\large o_{1}$ 的联合概率。步骤（2）是前向概率的递推公式，计算到时刻 t + 1 部分观测序列为 $\large o_{1}, o_{2}, ...,o_{t}, o_{t+1}$ 且在时刻 t +1 处于 $\large q_{i}$ 的前向概率，如下图 1 所示：

步骤（2）的方括号里，既然 $\large \alpha _{t}(j)$ 是到时刻 t 观测到 $\large o_{1}, o_{2}, ...,o_{t}$ ，并在时刻 t 处于状态 $\large q_{j}$ 的前向概率，那么乘积 $\large \alpha _{t}(j)a_{ji}$ 就是到时刻 t 观测到 $\large o_{1}, o_{2}, ...,o_{t}$ 并在时刻 t 处于状态 $\large q_{j}$ 而在时刻 t + 1 到达状态 $\large q_{i}$ 的联合概率。

对这个乘积在时刻 t 的所有可能的 N 个状态 $\large q_{j}$ 求和，其结果就是到时刻 t 观测为 $\large o_{1}, o_{2}, ...,o_{t}$ 并在 t + 1 处于状态 $\large q_{i}$ 的联合概率。

方括号里的值与观测概率 $\large b_{i}(o_{t+1})$ 的乘积恰好是到时刻 t + 1 观测到 $\large o_{1}, o_{2}, ...,o_{t}, o_{t+1}$ 并在时刻 t + 1 处于状态 $\large q_{i}$ 的前向概率 $\large \alpha _{t+1}(i)$ 。

步骤（3）给出P(O|λ ) 的计算公式。因为：

所以

如图2 所示，前向算法实际是基于 “状态序列的路径结构” 递推计算 P(O|λ ) 的算法。前向算法高效的关键是其局部计算前向概率，然后利用路径结构将前向概率 “递推” 到全局，得到 P(O|λ )。 具体地，在时刻 t = 1, 计算 $\large \alpha _{1}(i)$ 的 N 个值（i=1,2，...，N）而且每个 $\large \alpha _{t+1}(i)$ 的计算利用前一时刻 N 个 $\large \alpha _{t}(j)$ 。减少计算量的原因在于每一次计算直接引用前一个时刻的计算结果，避免重复计算。这样，利用前向概率计算 P(O|λ ) 的计算量是O(N^2 * T)阶的，而不是直接计算的 O(TN^T)阶。

通过一个例子，来说明前向计算的过程。

例2 考虑盒子和球的模型，状态集合 Q = {1,2,3}, 观测集合 V = {红，白}，

初始概率分布π + 状态转移概率分布 A+ 观测概率分布B 如下：

设 T = 3， O = （红，白，红），试用前向算法计算 P(O|λ)。

此例题属于要解决第一个问题：已知模型求观测序列出现的概率。

解：

（1）计算初始值，

第一次拿红球的概率

$\large \alpha _{1}(1) = \pi _{1}b_{1}(o_{1}) = 0.2 * 0.5 = 0.1$ —— 从1盒子拿红球，π：取1盒的概率；b1(o1)，拿取红球的概率

$\large \alpha _{1}(2) = \pi _{2}b_{2}(o_{1}) = 0.4 * 0.4 = 0.16$ —— 从2盒子拿红球，π：取2盒的概率；b2(o1)，拿取红球的概率

$\large \alpha _{1}(3) = \pi _{3}b_{3}(o_{1}) = 0.4 * 0.7 = 0.28$ —— 从3盒子拿红球，π：取3盒的概率；b3(o1)，拿取红球的概率

（2）递推计算

第二次拿白球的概率：

从1盒拿白球的概率：

$\large \alpha _2(1) [\sum_{i=1}^{3} \alpha _{1}(i)a_{i1}]b_{1}(o_{2}) = (0.1*0.5+0.16*0.3+0.28*0.2)*0.5=0.154*0.5=0.077$

解释：第二次从1盒拿白球的概率等于（上一次从1盒拿红球的概率乘以转移到1盒的概率 + 上一次从2盒拿红球的概率乘以转移到1盒的概率 + 上一次从3盒拿红球的概率转移到1盒的概率）求和后，再乘以从1盒拿白球的概率。

从2盒拿白球的概率：

$\large \dpi{120} \large \alpha _2(2) [\sum_{i=1}^{3} \alpha _{1}(i)a_{i2}]b_{2}(o_{2}) = (0.1*0.2+0.16*0.5+0.28*0.3)*0.6=0.184*0.6=0.1104$

从3盒拿白球的概率

$\large \alpha _2(3) [\sum_{i=1}^{3} \alpha _{1}(i)a_{i3}]b_{3}(o_{2}) = (0.1*0.3+0.16*0.2+0.28*0.5)*0.3=0.202*0.3=0.0606$

第三次拿红球的概率：

从1盒拿红球的概率：

$\large \alpha _{3}(1) = [\sum_{i=1}^{3}\alpha _{2}(i)a_{i1}]b_{1}(o_{3})=(0.077*0.5+0.1104*0.3+0.0606*0.2)*0.5=0.08374*0.5=0.04187$

从2盒拿红球的概率：

$\large \alpha _{3}(2) = [\sum_{i=1}^{3}\alpha _{2}(i)a_{i2}]b_{2}(o_{3})=(0.077*0.2+0.1104*0.5+0.0606*0.3)*0.4=0.08878*0.4=0.035512$

从3盒拿红球的概率：

$\large \alpha _{3}(3) = [\sum_{i=1}^{3}\alpha _{2}(i)a_{i3}]b_{3}(o_{3})=(0.077*0.3+0.1104*0.2+0.0606*0.5)*0.7=0.07548*0.7=0.052836$

（3）终止

代码如下：

# coding=utf-8
import numpy as np


class HiddenMarkov:
    def forward(self, Q, V, A, B, X, PI):
        N = len(Q)  # 状态集合的长度（几个盒子）
        M = len(X)  # 观测序列的长度（实验进行了几次）
        alphas = np.zeros((N, M))  # 前向概率矩阵 alphas 矩阵
        T = M  # 时刻长度，即观测序列的长度
        for t in range(T):  # 第 t 次
            indexOfXi = V.index(X[t])  # 观测值Xi 对应的 V中的索引，即是白球还是红球
            for i in range(N):  # 对每个状态(盒子)进行遍历
                if t == 0:  # 计算初值
                    alphas[i][t] = PI[t][i] * B[i][indexOfXi]  # 填充alphas的第0列，为第一次的概率计算
                    print("alphas_1(%d) = p%d * B%d(x1) = %f" % (i, i, i, alphas[i][t]))
                else:
                    # 计算两个数组的点积(列*列，求和，感觉很奇怪，但事实就是这样的，因为A与alpha就是列相乘)
                    alphas[i][t] = np.dot([alpha[t - 1] for alpha in alphas], [a[i] for a in A]) * B[i][indexOfXi]
                    print("alpha_%d(%d) = [sigma(i=0,..,%d ) alpha_%d(i)*ai%d] * B%d(x%d) = %f" % (t, i, len(A), t - 1, i, i, t, alphas[i][t]))
            print(alphas)

        P = sum(alpha[M - 1] for alpha in alphas)  # alphas的最后一列求和
        print("P = %f" % P)


Q = [1, 2, 3]
V = ['红', '白']
A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
X = ['红', '白', '红']
PI = [[0.2, 0.4, 0.4]]  # 声明为列数组，1列3行

hmm = HiddenMarkov()
hmm.forward(Q, V, A, B, X, PI)

结果如下：

alphas_1(0) = p0 * B0(x1) = 0.100000
alphas_1(1) = p1 * B1(x1) = 0.160000
alphas_1(2) = p2 * B2(x1) = 0.280000
[[0.1  0.   0.  ]
 [0.16 0.   0.  ]
 [0.28 0.   0.  ]]
alpha_1(0) = [sigma(i=0,..,3 ) alpha_0(i)*ai0] * B0(x1) = 0.077000
alpha_1(1) = [sigma(i=0,..,3 ) alpha_0(i)*ai1] * B1(x1) = 0.110400
alpha_1(2) = [sigma(i=0,..,3 ) alpha_0(i)*ai2] * B2(x1) = 0.060600
[[0.1    0.077  0.    ]
 [0.16   0.1104 0.    ]
 [0.28   0.0606 0.    ]]
alpha_2(0) = [sigma(i=0,..,3 ) alpha_1(i)*ai0] * B0(x2) = 0.041870
alpha_2(1) = [sigma(i=0,..,3 ) alpha_1(i)*ai1] * B1(x2) = 0.035512
alpha_2(2) = [sigma(i=0,..,3 ) alpha_1(i)*ai2] * B2(x2) = 0.052836
[[0.1      0.077    0.04187 ]
 [0.16     0.1104   0.035512]
 [0.28     0.0606   0.052836]]
P = 0.130218

2.3 后向算法

后向概率定义给定隐马尔可夫模型 λ ，定义在时刻 t 状态为 $\large q_{i}$ 的条件下，从 t+1 到 T 的部分观测序列为 $\large o_{t+1}, o_{t+2}, ..., o_{T}$ 的概率为后向概率，记作：

可以用递推的方法求得后向概率 $\large \beta _{t}(i)$ 及观测序列概率 $\large P(O|\lambda )$ 。

观测序列概率的后向算法：

输入：隐马尔可夫模型 λ，观测序列 O

输出：观测序列概率 $\large P(O|\lambda )$

（1）

解释：最后一次发生的概率都为1.

（2）对 t = T-1, T-2, ..., 1

解释：后一个状态（t + 1），由前面 t 的所有可能的状态转移过来。求和。

（3）

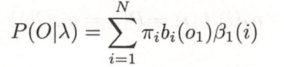
步骤（1）初始化后向概率，对最终时刻的所有状态 $\large q_{i}$ 规定 $\large \beta _{T}(i) = 1$ 。

步骤（2）是后向概率的递推公式。如图3所示。为了计算在时刻 t 、状态为 $\large q_{i}$ 的条件下，时刻 t + 1 之后的观测序列为 $\large o_{t+1}, o_{t+2}, ..., o_{T}$ 的后向概率 $\large \beta _{t}(i)$ ，只需考虑在时刻 t+1 所有可能的 N 个状态 $\large q_{j}$ 的转移概率（即 $\large a_{ij}$ 项），以及在此状态下的观测 $\large O_{t+1}$ 的观测概率（即 $\large b_{j(o_{t+1})}$ 项），然后考虑状态 $\large q_{j}$ 之后的观测序列的后向概率（即 $\large \beta _{t+1}(j)$ 项）。

步骤（3）求 $\large P(O|\lambda )$ 的思路，与步骤（2）一致，只是初始概率 $\large \pi _{i}$ 代替转移概率。

利用前向概率和后向概率的定义可以将观测序列 $\large P(O|\lambda )$ 统一写成：

例如：利用后向概率，求解上面的例题：

（1）初始最后一次取值，都默认为1.

beta3(1)=1

beta3(2)=1

beta3(3)=1

（2）预测倒数第三个球（红色），从哪里取出来 （字母角标表示第几行第几列，都从1开始。）

beta2(1)=(a11*b11*beta3(1) + a12*b21*beta3(2) + a13*b31*beta3(3)) 
= (0.50*0.50*1.00+ 0.20*0.40*1.00+ 0.30*0.70*1.00+ 0)=0.540 

(从1盒转移到1盒的概率 * 从1盒取红球的概率 * 上一步从1盒取球的概率  + 
从2盒转移到1盒的概率 * 从2盒取红球的概率 * 上一步从2盒取球的概率  + 
从3盒转移到1盒的概率 * 从3盒取红球的概率 * 上一步从3盒取球的概率) 

beta2(2)=(a21*b11*beta3(1) + a22*b21*beta3(2) + a23*b31*beta3(3))
= (0.30*0.50*1.00+ 0.50*0.40*1.00+ 0.20*0.70*1.00+ 0)=0.490

(从1盒转移到2盒的概率 * 从1盒取红球的概率 * 上一步从1盒取球的概率  + 
从2盒转移到2盒的概率 * 从2盒取红球的概率 * 上一步从2盒取球的概率  +
从3盒转移到1盒的概率 * 从3盒取红球的概率 * 上一步从3盒取球的概率) 

beta2(3)=(a31*b11*beta3(1) + a32*b21*beta3(2) + a33*b31*beta3(3)) 
= (0.20*0.50*1.00+ 0.30*0.40*1.00+ 0.50*0.70*1.00+ 0)=0.570

(从1盒转移到3盒的概率*从3盒取红球的概率*上一步从1盒取球的概率 + 
从2盒转移到3盒的概率*从2盒取红球的概率*上一步从2盒取球的概率 + 
从3盒转移到3盒的概率*从3盒取红球的概率*上一步从3盒取球的概率)

（3）预测倒数第二个球(白色)，从哪里来取出来
beta1(1)=(a11*b12*beta2(1) + a12*b22*beta2(2) + a12*b32*beta2(3)) 
= (0.50*0.50*0.54+ 0.20*0.60*0.49+ 0.30*0.30*0.57+ 0)=0.245
beta1(2)=(a21*b12*beta2(1) + a22*b22*beta2(2) + a23*b32*beta2(3)) 
= (0.30*0.50*0.54+ 0.50*0.60*0.49+ 0.20*0.30*0.57+ 0)=0.262
beta1(3)= (a31*b12*beta2(1) + a32*b22*beta2(2) + a33*b32*beta2(3)) 
= (0.20*0.50*0.54+ 0.30*0.60*0.49+ 0.50*0.30*0.57+ 0)=0.228

（4）预测倒数第一个球（红色），从哪里取出来

P(X|lambda) = 0.2 * 0.5 *0.245 + 0.4 * 0.4 * 0.262 + 0.4 * 0.7 * 0.228 = 0.130218

2.4 一些概率与期望值的计算

（这部分没看明白，先记录下来，万一以后有机会弄懂呢）

利用前向概率和后向概率，可以得到关于单个状态和两个状态概率的计算公式。

1. 给定模型 λ 和观测 O，在时刻 t 处于状态 $\large q_{i}$ 的概率。记为

可以通过前后向概率计算。事实上，

由前向概率 $\large \alpha _{t}(i)$ 和后向概率 $\large \beta _{t}(i)$ 定义可知：

于是得到：

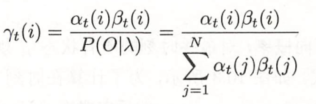
2. 给定模型 λ 和观测 O ，在时刻 t 处于状态 $\large q_{i}$ 且在时刻 t + 1, 处于 $\large q_{j}$ 的概率：

可以通过前向后向概率计算：

而

所以

3. 将 $\large \gamma _{t}(i)$ 和 $\large \zeta _{t}(i, j)$ 对应各个时刻 t 求和，可以得到一些有用的期望值。

（1）在观测O下，状态 i 出现的期望值：

（2）在观测O 下，由状态 i 转移的期望值：

（3）在观测 O 下，由状态转移到状态 j 的期望值：

3 学习算法

隐马尔可夫模型的学习，根据训练数据是包括观测序列和对应的状态序列还是只有观测序列，可以分别由监督学习与无监督学习（Baum-Welch 即 EM 算法）实现。有监督学习可以解决隐马尔可夫模型的第二个问题：已知观测序列，求模型的参数

3.1 监督学习算法

假设已给训练数据包含 S 个长度相同的观测序列和对应的状态序列， $\large \{(O_{1}, I_{1}), (O_{2},I_{2}), ..., (O_{s}, I_{s})\}$ （可以理解为：知道哪次从哪个盒子拿出哪种球）。那么可以利用极大似然估计法来估计隐马尔可夫模型的参数。

1 转移概率 $\large a_{ij}$ 的估计，即从i 转移到 j 的概率。

设样本中，时刻 t 处于状态 i，时刻 t + 1 转移到状态 j 的频数为 $\large A_{ij}$ ，那么状态转移概率 $\large a_{ij}$ 的估计是：

解释：在整个S 序列中，查到 Aij 出现的次数，然后计算 Ai 转移到所有 j 的次数，前者占后者的百分比，即为aij。

2 观测概率 $\large b_{j}(k)$ 的估计

设样本中状态为 j（盒子），并观测为 k（红白球）的频数是 $\large B_{jk}$ （j 盒子取出 k颜色球的个数），那么状态为 j 观测为 k 的概率 $\large b_{j}(k)$ 的估计是：

解释：j 盒子取出 k颜色球的次数，占总体情况（从 j 盒子取出的所有球次数）的比值。

3 初始状态概率 $\large \pi _{i}$ 的估计 $\large \hat{\pi } _{i}$ 为 S 个样本初始状态为 $\large q_{i}$ 的频率

（解释：根据已知的S序列，可以求出每个盒子中每种球出现的频率，即可以当做概率 πi）

由于监督学习需要使用标注的训练数据，而人工标注训练数据往往代价很高，有时就会利用无监督学习的方法。

3.2 Baum-Welch算法

【此部分先跳过，太难懂了。】

假设给定训练数据，只包含S个长度为T的观测序列 { $\large O_{1},O_{2},...,O_{S}$ }, 而没有对应的状态序列，目标是学习隐马尔可夫模型的参数。将观测序列数据看做观测数据 O，状态序列数据看做不可观测的隐藏数据 I ，那么隐马尔可夫模型事实上，是一个含有隐变量的概率模型：

它的参数学习可以由EM 算法实现。

1 确定完全数据的对数似然函数

2 EM 算法的E 步：

......

3.3 标注偏置问题

https://blog.csdn.net/lskyne/article/details/8669301

4 预测算法

下面介绍隐马尔可夫模型预测的两种算法：近似算法与维特比算法（Viterbi algorithm）

这是解决隐马尔可夫模型的第三个问题：已知观测序列求可能的状态序列

4.1 近似算法

近似算法的思想是：在每个时刻 t 选择在该时刻最有可能出现的状态 $\large i_{t}^{*}$ ，从而得到一个状态序列 $\large I^{*} = \{i_{1}^{*}, i_{2}^{*}, ..., i_{T}^{*}\}$ , 将它作为预测的结果。

给定隐马尔可夫模型 λ 和观测序列 O，在时刻 t 处于状态 $\large q_{i}$ 的概率 $\large \gamma _{t}(i)$ 是：

在每一时刻 t 最有可能的状态 $\large i_{t}^{*}$ 是：

从而得到状态序列 $\large I^{*} = \{i_{1}^{*}, i_{2}^{*}, ..., i_{T}^{*}\}$ 。

近似算法的优点是计算简单，其缺点是不能保证预测的状态序列整体是最有可能的状态序列，因为预测的状态序列可能有实际不发生的部分。事实上，上述方法得到的状态序列中，有可能存在转移概率为 0 的相邻状态，即对某些 i, j, aij = 0 时。尽管如此，近似算法仍然是有用的。

4.2 维特比算法（Viterbi algorithm）

4.2.1 先铺垫一个例子，有助于理解后面的概念及公式。

例子 3 已知模型，观测序列 O=（红，白，红），试求最优状态序列，即最优路径

解：理解好题目，其实求最优路径，也就是求，抽取盒子的顺序。

（1）初始化，在 t = 1时，对每一个状态 i ，i = 1,2,3，求状态为 i 的观测 $\large o_{1}$ 为红球的概率，记此概率为 $\large \delta _{1}(i)$ ，则：

第一次从1盒抽红球的概率： $\large \delta _{1}(1) = \pi _{1}b_{1}(o_{1}) = 0.2*0.5 = 0.1$
第一次从2盒抽红球的概率： $\large \delta _{1}(2) = \pi _{2}b_{2}(o_{1}) = 0.4*0.4 = 0.16$
第一次从3盒抽红球的概率： $\large \delta _{1}(3) = \pi _{3}b_{3}(o_{1}) = 0.4*0.7 = 0.28$

记 $\large \psi _{1}(i) = 0$ ， i = 1,2,3. 因为开始不知道是从哪个盒子开始的，此处先设为0.

（2）在 t = 2 时（即第二次抽取），（i = 1,2,3）, 求在 t = 1 时状态（把状态理解为：盒子几）为 j 观测为红并在 t = 2 时，状态为 i，观测 $\large o_{2}$ 为白球的路径的最大概率。（通俗讲：第t次为i 盒子的红球，第j次为白球，求 j 是哪个盒子的最大概率）。记此最大概率为 $\large \delta _{2}(i)$ ，则：

从上次抽盒结果分别转移到 1盒抽取白球的概率，取最大概率：

$\delta_{2}(1) = max(\delta_{1}(1)*a_{11}, \delta_{1}(2)*a_{21}, \delta_{1}(3)*a_{31})*0.5 = max(0.10*0.5, 0.16*0.3, 0.28*0.2)*0.5=0.056*0.5=0.028$

$\large \psi_{2}(1) = 3$ —— 1盒的第二次转移，从3盒子转移过来的概率最大，所以取3盒子。

从上次抽盒结果分别转移到 2盒抽取白球的概率，取最大概率：

$\large \delta_{2}(2) = max(\delta_{1}(1)*a_{12}, \delta_{1}(2)*a_{22}, \delta_{1}(3)*a_{32})*0.5 = max(0.10*0.2, 0.16*0.5, 0.28*0.3)*0.6=0.084*0.6=0.0504$

$\large \psi_{2}(2) = 3$ —— 2盒的第二次转移，从3盒子转移过来的概率最大，所以取3盒子

从上次抽盒结果分别转移到 3盒抽取白球的概率，取最大概率：

$\large \delta_{2}(3) = max(\delta_{1}(1)*a_{13}, \delta_{1}(2)*a_{23}, \delta_{1}(3)*a_{33})*0.3 = max(0.10*0.3, 0.16*0.2, 0.28*0.5)*0.3=0.14*0.3=0.042$

$\large \psi_{2}(3) = 3$ —— 3盒的第二次转移，从3盒子转移过来的概率最大，所以取3盒子

（3）同样，在 t = 3 时，

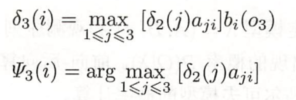
从上次抽盒结果分别转移到 1盒抽取白球的概率，取最大概率：

$\large \delta_{3}(1) = max(\delta_{2}(1)*a_{11}, \delta_{2}(2)*a_{21}, \delta_{2}(3)*a_{31})*0.5 = max(0.028*0.5, 0.0504*0.3, 0.042*0.2)*0.5=0.01512*0.5=0.00756$

$\large \psi_{3}(1) = 2$ ——1盒的第3次转移，从2盒子转移过来的概率最大。

从上次抽盒结果分别转移到 2盒抽取白球的概率，取最大概率：

$\large \delta_{3}(2) = max(\delta_{2}(1)*a_{21}, \delta_{2}(2)*a_{22}, \delta_{2}(3)*a_{32})*0.4 = max(0.028*0.2, 0.0504*0.5, 0.042*0.3)*0.4=0.0252*0.4=0.01008$

$\large \psi_{3}(2) = 2$ ——2盒的第3次转移，从2盒子转移过来的概率最大。

从上次抽盒结果分别转移到 3盒抽取白球的概率，取最大概率：

$\large \delta_{3}(3) = max(\delta_{2}(1)*a_{31}, \delta_{2}(2)*a_{32}, \delta_{2}(3)*a_{33})*0.7 = max(0.028*0.3, 0.0504*0.2, 0.042*0.5)*0.7=0.021*0.7=0.0147$

$\large \psi_{3}(3) = 3$ ——3盒的第3次转移，从3盒子转移过来的概率最大。

（4） 以 P* 表示最优路径的概率，则， P* = max (0.0147, 0.01008, 0.007056) = 0.0147,

最优路径的终点是 $\large i_{3}^{*} = arg max[\delta _{3}(i)] = \psi _{3}(3) = 3$

（5） 由最优路径的终点，i*3, 逆向找到 i*2, i*1:

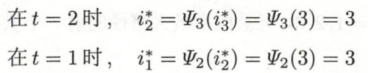
于是，求的最优路径，即为最优状态序列

代码：

class HiddenMarkov:
    def viterbi(self, Q, V, A, B, X, PI):
        N = len(Q)  # 状态集合的长度（几个盒子）
        M = len(X)  # 观测序列的长度（实验进行了几次）
        deltas = np.zeros((N, M))  # 前向概率矩阵 alphas 矩阵
        psis = np.zeros((N, M))  # 记录路径, 存储的每一次概率最大的值盒子
        Y = np.zeros((1, M))  # 最优(概率最大)的状态序列
        for t in range(M):  # 第t次
            realT = t + 1  # 状态号从1开始
            indexofXi = V.index(X[t])
            for i in range(N):  # 第 i 个盒子
                realI = i + 1   # 盒子号从1开始
                if t == 0:    # 第一次取球
                    deltas[i][0] = PI[0][i] * B[i][indexofXi]    # 初始值
                    psis[i][0] = 0  # 第一次初始psis[i][0]为0
                    print("delta_1(%d) = pi_%d * B%d(x1) = %.2f * %.2f = %.2f" % (realI, realI, realI, PI[0][i], B[i][indexofXi], deltas[i][0]))
                    print('psis_1(%d) = 0' % realT)    # 第一次没有决定从哪个盒子取，所以先定为0
                    print()
                else:
                    deltas[i][t] = np.max(
                        np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A])
                    ) * B[i][indexofXi]
                    temp = np.max(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A]))  # 保存最大值
                    print("delta_%d(%d) = max[delta_%d(j) * Aj%d] * B%d(x%d) = %.2f * %.2f = %.5f" % (realT, realI, t, realI, realI, realT, temp, B[i][indexofXi], deltas[i][t]))
                    psis[i][t] = np.argmax(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A])) + 1
                    print("psis_%d(%d) = argmax[delta_%d(j)Aj%d] = %d" % (realT, realI, t, realI, psis[i][t]))
                    print()
        print("deltas: \n", deltas)
        print("psis:\n", psis)
        print()
        # 最后一列的最大值的索引
        Y[0][M-1] = np.argmax([delta[M-1] for delta in deltas]) + 1  # 序号从1开始， 沿着给定轴，返回最大值的索引。
        print("Y[0][M-1]: \n", Y[0][M-1])
        print("Y%d=argmax[deltaT(i)]=%d" % (M, Y[0][M-1]))  # 最优路径的终点
        print()
        for t in range(M-2, -1, -1):  # 逆向推导最优路径， 倒着扫描，间隔为1。填充Y时，也倒着填充
            Y[0][t] = psis[int(Y[0][t+1]) - 1][t+1]    # psis的索引
            print("Y%d = psis%d(Y%d) = %d" % (t+1, t+2, t+2, Y[0][t]))
            print()
        print("最大概率的状态序列 Y 是：", Y)


Q = [1, 2, 3]
V = ['红', '白']
A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
X = ['红', '白', '红']
PI = [[0.2, 0.4, 0.4]]  # 声明为列数组，1行3列

hmm = HiddenMarkov()
hmm.viterbi(Q, V, A, B, X, PI)

结果：

delta_1(1) = pi_1 * B1(x1) = 0.20 * 0.50 = 0.10
psis_1(1) = 0

delta_1(2) = pi_2 * B2(x1) = 0.40 * 0.40 = 0.16
psis_1(1) = 0

delta_1(3) = pi_3 * B3(x1) = 0.40 * 0.70 = 0.28
psis_1(1) = 0

delta_2(1) = max[delta_1(j) * Aj1] * B1(x2) = 0.06 * 0.50 = 0.02800
psis_2(1) = argmax[delta_1(j)Aj1] = 3

delta_2(2) = max[delta_1(j) * Aj2] * B2(x2) = 0.08 * 0.60 = 0.05040
psis_2(2) = argmax[delta_1(j)Aj2] = 3

delta_2(3) = max[delta_1(j) * Aj3] * B3(x2) = 0.14 * 0.30 = 0.04200
psis_2(3) = argmax[delta_1(j)Aj3] = 3

delta_3(1) = max[delta_2(j) * Aj1] * B1(x3) = 0.02 * 0.50 = 0.00756
psis_3(1) = argmax[delta_2(j)Aj1] = 2

delta_3(2) = max[delta_2(j) * Aj2] * B2(x3) = 0.03 * 0.40 = 0.01008
psis_3(2) = argmax[delta_2(j)Aj2] = 2

delta_3(3) = max[delta_2(j) * Aj3] * B3(x3) = 0.02 * 0.70 = 0.01470
psis_3(3) = argmax[delta_2(j)Aj3] = 3

deltas: 
 [[0.1     0.028   0.00756]
 [0.16    0.0504  0.01008]
 [0.28    0.042   0.0147 ]]
psis:
 [[0. 3. 2.]
 [0. 3. 2.]
 [0. 3. 3.]]

Y[0][M-1]: 
 3.0
Y3=argmax[deltaT(i)]=3

Y2 = psis3(Y3) = 3

Y1 = psis2(Y2) = 3

最大概率的状态序列 Y 是： [[3. 3. 3.]]

4.2.2 概念

维特比算法实际是用动态规划解隐马尔可夫预测模型问题，即用动态规划概率最大路径（最优路径）。这时一条路径对应着一个状态序列（盒子序列）。

根据动态规划原理，最优路径具有这样的特性：

如果最优路径在时刻 t 通过结点 $\large i_{t}^{*}$ ,那么这一路经从结点 $\large i_{t}^{*}$ 到终点 $\large i_{T}^{*}$ 的部分路径，对于从 $\large i_{t}^{*}$ 到 $\large i_{T}^{*}$ 的所有可能的部分路径来说，必须是最优的。因为加入不是这样，那么从 $\large i_{t}^{*}$ 到 $\large i_{T}^{*}$ 就有另一条更好的部分路径存在，如果把它和从 $\large i_{1}^{*}$ 到达 $\large i_{t}^{*}$ 的部分路径连接起来，就会形成一条比原来的路径更优的路径，这是矛盾的。

依据这一原理，只需要从时刻 t = 1 开始，递推地计算在时刻 t 状态为 i 的各条部分路径的最大概率，直至得到 t = T 状态为 i 的各条路径的最大概率。时刻 t = T 的最大概率，即为最优路径的概率 P*，最优路径的终点 $\large i_{T}^{*}$ 也同时得到。之后，为了找出最优路径的各个结点，从终点 $\large i_{T}^{*}$ 开始，右后向前逐步求得结点 $\large i_{T-1}^{*}, i_{T-2}^{*},......, i_{1}^{*},$ 得到最优路径 $\large I^{*} = (i_{1}^{*}, i_{2}^{*}, ..., i_{T}^{*})$ ，这就是维特比算法。