一隐马尔可夫模型的基本概念

（1）隐马尔可夫模型的定义

隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列（state sequence);每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列（observation sequence)。序列的每一个位置又可以看作是一个时刻。

隐马尔科夫链简单说来，就是把时间线看做一条链，每个节点只取决于前N个节点。

隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。

隐马尔可夫模型的形式定义如下：

设 $\boldsymbol{Q}$ 是所有可能的状态的集合， $\boldsymbol{V}$ 是所有可能的观侧的集合，N是可能的状态数，M是可能的观测数.

$\boldsymbol{Q}=\left \{ q_{1} ,q_{2},.....,q_{N}\right \}$ ， $\boldsymbol{V}=\left \{ v_{1} ,v_{2},.....,v_{M}\right \}$

$\boldsymbol{I}$ 是长度为 $\boldsymbol{T}$ 的状态序列， $\boldsymbol{O}$ 是对应的观测序列.

$\boldsymbol{I}=\left \{ i_{1} ,i_{2},.....,i_{T}\right \}$ ， $\boldsymbol{O}=\left \{ o_{1} ,o_{2},.....,o_{T}\right \}$

隐马尔可夫模型由初始状态概率向量 $\boldsymbol{\pi}$ 、状态转移概率矩阵 $\boldsymbol{A}$ 和观测概率矩阵 $\boldsymbol{B}$ 决定。 $\boldsymbol{\pi}$ 和 $\boldsymbol{A}$ 决定状态序列， $\boldsymbol{B}$ 决定观测序列。隐马尔可夫模型 $\boldsymbol{\lambda }$ 可以用三元符号表示，即 $\boldsymbol{\lambda } = \left ( \boldsymbol{A},\boldsymbol{B},\boldsymbol{\pi } \right )$ $\boldsymbol{A}$ ， $\boldsymbol{B}$ ， $\boldsymbol{\pi}$ 称为隐马尔可夫模型的三要素。

状态转移概率矩阵 $\boldsymbol{A}$ 与初始状态概率向量 $\boldsymbol{\pi}$ 确定了隐藏的马尔可夫链，生成不可观测的状态序列。观测概率矩阵 $\boldsymbol{B}$ 确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。

$\boldsymbol{A}$ 是状态转移概率矩阵:

$\boldsymbol{A} = \left [ \boldsymbol{a_{ij}} \right ]_{N\times N}$

其中 $\boldsymbol{a_{ij}} = \boldsymbol{P}\left ( i_{i+1} = q_{j} | i_{i} = q_{i} \right )$ 是在时刻 $\boldsymbol{t}$ 处于状态 $\boldsymbol{q_{i}}$ 的条件下在时刻 $\boldsymbol{t}$ +1转移到状态 $\boldsymbol{q_{j}}$ 的概率。

$\boldsymbol{B}$ 是观测概率矩阵:

$\boldsymbol{B} = \left [ \boldsymbol{b_{j}\left (k \right )} \right ]_{N\times M}$

其中 $\boldsymbol{b_{j}\left (k \right )} = \boldsymbol{P}\left ( o_{t} = v_{k} | i_{t} = q_{j} \right )$ 是在时刻 $\boldsymbol{t}$ 处于状态 $\boldsymbol{q_{j}}$ 的条件下生成观测 $\boldsymbol{v_{k}}$ 的概率。

$\boldsymbol{\pi}$ 是初始状态概率向量:

$\boldsymbol{\pi}$ = ( $\boldsymbol{\pi_{i}}$ )

其中 $\boldsymbol{\pi_{i}}$ = $\boldsymbol{P\left ( i_{1} = q_{i} \right )}$ 是时刻 $\boldsymbol{t = 1}$ 处于状态 $\boldsymbol{q_{i}}$ 的概率。

隐马尔可夫模型的例子：

（2）观测序列的生成过程

（3）隐马尔可夫模型的3个基本问题

(1)概率计算问题。给定模型 $\boldsymbol{\lambda } = \left ( \boldsymbol{A},\boldsymbol{B},\boldsymbol{\pi } \right )$ 和观测序列 $\boldsymbol{O}=\left \{ o_{1} ,o_{2},.....,o_{T}\right \}$ ，计算在模型l $\boldsymbol{\lambda }$ 之下观测序列 $\boldsymbol{O}$ 出现的概率。

(2)学习问题。己知观测序列 $\boldsymbol{O}=\left \{ o_{1} ,o_{2},.....,o_{T}\right \}$ ，估计模型参数 $\boldsymbol{\lambda } = \left ( \boldsymbol{A},\boldsymbol{B},\boldsymbol{\pi } \right )$ ，使得在该模型下观测序列概率 $\boldsymbol{P\left ( O|\lambda \right )}$ 最大。即用极大似然估计的方法估计参数。

(3)预测问题。也称为解码(decoding)问题。己知模型和观测序列 $\boldsymbol{O}=\left \{ o_{1} ,o_{2},.....,o_{T}\right \}$ ，求对给定观测序列条件概率 $\boldsymbol{P\left ( I|O \right )}$ 最大的状态序列 $\boldsymbol{I}=\left \{ i_{1} ,i_{2},.....,i_{T}\right \}$ ，即给定观测序列，求最有可能的对应的状态序列。

二概率计算算法

（1）观测序列概率的前向算法

前向概率定义：给定隐马尔可夫模型 $\boldsymbol{\lambda }$ ，定义到时刻 $\boldsymbol{t}$ 部分观测序列为 $o_{1} ,o_{2},.....,o_{t}$ 且状态为 $\boldsymbol{q_{i}}$ 的概率为前向概率，记作

$\boldsymbol{\alpha _{t}\left (i \right )} = \boldsymbol{P}\left ( o_{1} ,o_{2},.....,o_{t}, i_{t} = q_{i} |\lambda \right )$

可以递推地求得前向概率 $\boldsymbol{\alpha _{t}\left (i \right )}$ 及观测序列概率 $\boldsymbol{P\left ( O|\lambda \right )}$

观测序列概率的前向算法：

输入：HMM的参数 $\boldsymbol{\lambda }$ ，观测序列 $\boldsymbol{O}$ ；
输出：观测序列概率 $\boldsymbol{P\left ( O|\lambda \right )}$ .

(1)初值

$\boldsymbol{\alpha _{1}\left (t \right )} =$ $\boldsymbol{\pi _{i}{b _{i}(o_{1})}}, i=1,2,\cdots ,N$

(2)递推：对 $\boldsymbol{t = 1,2,\cdots ,T-1}$ ,

$\boldsymbol{\alpha _{t+1}\left (i \right )} =$ $\left [ \sum_{j=1}^{N}\alpha _{t}(j)\alpha _{ji} \right ]$ $\boldsymbol{{b _{i}(o_{t+1})}}, i=1,2,\cdots ,N$

(3)终止

$\boldsymbol{P\left ( O|\lambda \right )}$ = $\boldsymbol{\sum_{i=1}^{N}\alpha _{T}(i)}$

（2）观测序列概率的后向算法

后向概率定义：给定隐马尔可夫模型 $\boldsymbol{\lambda }$ ，定义到时刻 $\boldsymbol{t}$ 状态为 $\boldsymbol{q_{i}}$ 的条件下，从 $\boldsymbol{t+1}$ 到 $\boldsymbol{T}$ 的部分观测序列为 $o_{t+1} ,o_{t+2},.....,o_{T}$ 的概率为后向概率，记作

$\boldsymbol{\beta _{t}\left (i \right )} = \boldsymbol{P}\left ( o_{t+1} ,o_{t+2},.....,o_{T}, i_{t} = q_{i} |\lambda \right )$

可以递推地求得前向概率 $\boldsymbol{\beta _{t}\left (i \right )}$ 及观测序列概率 $\boldsymbol{P\left ( O|\lambda \right )}$

观测序列概率的后向算法：

输入：HMM的参数 $\boldsymbol{\lambda }$ ，观测序列 $\boldsymbol{O}$ ；
输出：观测序列概率 $\boldsymbol{P\left ( O|\lambda \right )}$ .

(1)初值

$\boldsymbol{\beta _{T}\left (i \right )} = 1$ ， $i=1,2,\cdots ,N$

(2)递推：对 $\boldsymbol{t = T-1,T-2,\cdots ,1}$ ,

$\boldsymbol{\beta _{t}\left (i \right )} =$ $\boldsymbol{\sum_{j=1}^{N}a_{ij}b_{j}(o_{t+1})\beta _{t+1}(j)}$ ， $i=1,2,\cdots ,N$

(3)终止

$\boldsymbol{P\left ( O|\lambda \right )}$ = $\boldsymbol{\sum_{i=1}^{N}\pi _{i}b _{i}(o_{1})\beta _{1}(i)}$

（3）前向算法和后向算法实例

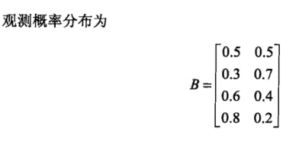
考虑盒子和球模型 $\boldsymbol{\lambda } = \left ( \boldsymbol{A},\boldsymbol{B},\boldsymbol{\pi } \right )$ ，状态集合 $\boldsymbol{Q = \left \{1,2,3 \right \}}$ ，观测序列 $\boldsymbol{V=}$ {红，白}，

A = [0.5，0.2，0.3 B=[0.5，0.5 $\boldsymbol{\pi = \left ( 0.2,0.4,0.4 \right )^{T}}$

0.3，0.5，0.2 0.4，0.6

0.2，0.3，0.5] 0.7，0.3]

设T=3，O=（红，白，红），试分别用前向和后向算法计算 $\boldsymbol{P\left ( O|\lambda \right )}$

from numpy import *
import numpy as np
import matplotlib as plt
import math

class HMM:
    def __init__(self, pi, A, B):
        self.pi = pi
        self.A = A
        self.B = B
        self.M = B.shape[1]
        self.N = A.shape[0]


def forward(hmm, obs):
    T = len(obs)  # 观察序列长度
    N = hmm.N  # 隐藏层状态数
    alpha = matrix(zeros((N, T)))  # 前向概率
    alpha[:, 0] = multiply(hmm.pi[:], hmm.B[:, observation.index(obs[0])])  # 初值
    for t in range(1, T):  # 递推
        for n in range(0, N):
            alpha[n, t] = sum(alpha[:, t - 1].T * hmm.A[:, n]) * hmm.B[n, observation.index(obs[t])]
    prob = sum(alpha[:, T - 1])  # 计算观察序列概率
    return prob, alpha

def backward(hmm, obs):
    T = len(obs)    # 观察序列长度
    N = hmm.N       # 隐藏层状态数
    beta = matrix(zeros((N,T)))    # 后向概率
    beta[:,T-1] = 1
    for t in reversed(range(0,T-1)):
        for n in range(0,N):
            beta[n,t] = sum(multiply(multiply(hmm.A[n,:].T, hmm.B[:,observation.index(obs[t+1])]), beta[:,t+1]))
    prob = sum(multiply(multiply(hmm.pi, hmm.B[:,observation.index(obs[0])]), beta[:,0]))
    return prob, beta

if __name__ == "__main__":
    # 状态转移概率矩阵
    A = matrix([[0.5,0.2,0.3],
                [0.3,0.5,0.2],
                [0.2,0.3,0.5]])
    # 观测概率矩阵
    B = matrix([[0.5,0.5],
                [0.4,0.6],
                [0.7,0.3]])
    pi = matrix([0.2,0.4,0.4]).T
    hmm = HMM(pi, A, B)
    observation = ['red','write']# 所有可能的观测集合
    observed = ['red','write','red']# 观测序列
    prob, alpha = forward(hmm, observed)
    prob, beta = backward(hmm, observed)
    print('The forword probability is: \n', alpha)
    print('The probability of this observed sequence is %f' % prob)
    print('The forword probability is: \n', beta)
    print('The probability of this observed sequence is %f' % prob)

运行结果：

三学习算法

隐马尔可夫模型的学习根据训练数据的不同分为监督学习和非监督学习。

监督学习：训练数据包括观测序列和对应的状态序列

非监督学习：训练数据仅有观测序列

（1）监督学习

假设已给训练数据包含S个长度相同的观测序列和对应的状态序列 $\boldsymbol{\left \{ \left ( O_{1},I_{1} \right ), \left ( O_{2},I_{2} \right ),\cdots ,\left ( O_{S},I_{S} \right )\right \}}$ ，那么可以利用极大似然估计法来估计隐马尔可夫模型的参数。

1.转移概率 $\boldsymbol{a_{ij}}$ 的估计

设样本中时刻 $\boldsymbol{t}$ 处于状态 $\boldsymbol{i}$ 时刻 $\boldsymbol{t+1}$ 处于状态j的频数为 $\boldsymbol{A_{ij}}$ ，那么状态转移概率 $\boldsymbol{a_{ij}}$ 的估计是

$\boldsymbol{\hat{a_{ij}}=\frac{A_{ij}}{\sum_{j=1}^{N}A_{ij}}, i=1,2,\cdots ,N;j=1,2,\cdots ,N}$

2，观测概率 $\boldsymbol{b_{j}(k)}$ 的估计

设样本中状态为 $\boldsymbol{j}$ 且观测为 $\boldsymbol{k}$ 的频数是 $\boldsymbol{B_{jk}}$ ，那么状态为 $\boldsymbol{j}$ 且观测为 $\boldsymbol{k}$ 的概率 $\boldsymbol{b_{j}(k)}$ 的估计是

$\boldsymbol{\hat{b_{j}}(k)=\frac{B_{jk}}{\sum_{k=1}^{M}B_{jk}}, j=1,2,\cdots ,N;k=1,2,\cdots ,M}$

3，初始状态概率 $\boldsymbol{\pi _{i}}$ 的估计 $\boldsymbol{\hat{\pi _{i}}}$ 为S个样本中初始状态为 $\boldsymbol{q_{i}}$ 的频率。

由于监督学习需要使用训练数据，而人工标注训练数据往往代价很高，所以有时会利用非监督学习的方法。

（2）非监督学习

非监督学习用的是Baum-welch算法，这个算法其实就是EM算法。

现在假设给定的训练数据只包含 $\boldsymbol{S}$ 个长度为 $\boldsymbol{T}$ 的观测序列 $\boldsymbol{\left \{ O_{1}, O_{2},\cdots ,O_{S}\right \}}$ 而没有对应的状态序列，然后目标是学习隐马尔可夫模型 $\boldsymbol{\lambda } = \left ( \boldsymbol{A},\boldsymbol{B},\boldsymbol{\pi } \right )$ 的参数。

我们将观测序列数据看做观测数据 $\boldsymbol{O}$ ，状态序列数据看做不可观测的隐数据 $\boldsymbol{I}$ ，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型

$\boldsymbol{P(O|\lambda )=\sum_{I}P(O|I,\lambda)P(I|\lambda )}$

它的参数学习可以由EM算法实现.

推导：

1.确定完全数据的对数似然函数

把所有观测数据写成 $\boldsymbol{O=\left \{ O_{1}, O_{2},\cdots ,O_{T}\right \}}$ ，所有隐数据写成 $\boldsymbol{I=\left \{ i_{1}, i_{2},\cdots ,i_{T}\right \}}$ ，完全数据是 $\boldsymbol{(O,I)=\left \{ o_{1}, o_{2},\cdots ,o_{T} ,i_{1}, i_{2},\cdots ,i_{T}\right \}}$ 。完全数据的对数似然函数是 $\boldsymbol{logP(O,I|\lambda )}$ 。

2.EM算法的E步，求Q函数 $\boldsymbol{Q(\lambda ,\bar{\lambda })}$

$\boldsymbol{Q(\lambda ,\bar{\lambda })=\sum_{I}P(O,I|\lambda)P(O,I|\bar{\lambda })}$

其中， $\bar{\lambda }$ 是隐马尔可夫模型参数的当前估计值，λ是要极大化的隐马尔可夫模型参数。

$\boldsymbol{P(O,I|\lambda)=\pi _{i_{1}}b_{i_{1}}(o_{1})a_{i_{1}i_{2}}b_{i_{2}}(o_{2})\cdots a_{i_{T-1}i_{T}}b_{i_{T}}(o_{T})}$

于是，函数 $\boldsymbol{Q(\lambda ,\bar{\lambda })}$ 可以写成

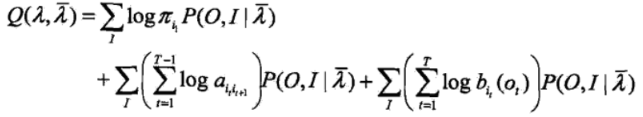
上式中的求和都是对所有训练数据的序列总长度T进行的。

3.EM算法的M步：极大化 $\boldsymbol{Q(\lambda ,\bar{\lambda })}$ 求模型参数A, B,π

4.Baum-welch模型参数的估计公式

Baum-welch算法

输入：观测数据 $\boldsymbol{O=\left \{ O_{1}, O_{2},\cdots ,O_{T}\right \}}$ ；

输出：隐马尔可夫模型参数。

过程：

四预测算法

维特比算法实际是用动态规划解隐马尔可夫模型预侧问题，即用动态规划(dynamic programming)求概率最大路径(最优路径)。一条路径对应着一个状态序列。

根据动态规划原理，最优路径具有这样的特性：如果最优路径在时刻t通过结点 $\boldsymbol{i_{t}^{\ast }}$ ，那么这一路径从结点 $\boldsymbol{i_{t}^{\ast }}$ 到终点 $\boldsymbol{i_{T}^{\ast }}$ 的部分路径，对于从 $\boldsymbol{i_{t}^{\ast }}$ 到 $\boldsymbol{i_{T}^{\ast }}$ 的所有可能的部分路径来说，必须是最优的。依据这一原理，我们只需从时刻t=1开始，递推地计算在时刻t状态为i的各条部分路径的最大概率，直至得到时刻t=T状态为i的各条路径的最大概率。时刻t=T的最大概率即为最优路径的概率P*。

最优路径的终结点 $\boldsymbol{i_{T}^{\ast }}$ 也同时得到。之后，从终结点 $\boldsymbol{i_{T}^{\ast }}$ 开始，由后向前逐步求得结点 $\boldsymbol{i_{T-1}^{\ast },\cdots,i_{1}^{\ast }}$ 。

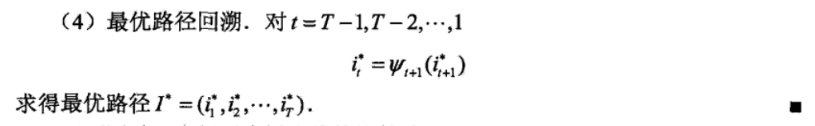
维特比算法的实例：

# -*-coding:utf-8-*-
import numpy as np

# 隐马尔可夫模型λ=(A, B, pai)
# A是状态转移概率分布，状态集合Q的大小N=np.shape(A)[0]
# 从下给定A可知：Q={盒1, 盒2, 盒3}, N=3
A1 = np.array([[0.5, 0.2, 0.3],
              [0.3, 0.5, 0.2],
              [0.2, 0.3, 0.5]])
# B是观测概率分布，观测集合V的大小T=np.shape(B)[1]
# 从下面给定的B可知：V={红，白}，T=2
B1 = np.array([[0.5, 0.5],
              [0.4, 0.6],
              [0.7, 0.3]])
# pai是初始状态概率分布，初始状态个数=np.shape(pai)[0]
pi1 = np.array([[0.2],
                [0.4],
                [0.4]])
# 观测序列
Object1 = np.array([[0],
              [1],
              [0]])  # 0表示红色，1表示白，就是(红，白，红)观测序列

def sum(L):
    sumValue = 0.0
    for i in range(0, len(L)):
        sumValue += L[i]
    return sumValue
def max(L):
    target = 0
    maxValue = L[target]
    for i in range(1, len(L)):
        if (L[i] > maxValue):
            target = i
            maxValue = L[i]
    return maxValue, target + 1

def printTable(table, type="float"):
    if (type == "float"):
        for i in range(0, len(table)):
            for j in range(0, len(table[i])):
                print ("%-16f" % (table[i][j]),)
            print ("\n")
    elif (type == "int"):
        for i in range(0, len(table)):
            for j in range(0, len(table[i])):
                print ("%-2d" % (table[i][j]),)
            print ("\n")


def initTable(x, y, type="float"):
    table = []
    if (type == "float"):
        initValue = 0.0
    elif (type == "int"):
        initValue = 0
    for i in range(0, x):
        temp = []
        for j in range(0, y):
            temp.append(initValue)
        table.append(temp)
    return np.array(table)

def forwardV(A, B, pi, Object, mod="forward"):
    T = len(Object)
    NumState = len(A)
    NodeTable = initTable(NumState, T)
    if (mod == "viterbi"):
        NodePath = initTable(NumState, T, type="int")
    for i in range(0, NumState):
        NodeTable[i][0] = pi[i] * B[i][Object[0]]
    for t in range(1, T):
        for j in range(0, NumState):
            temp = []
            for i in range(0, NumState):
                temp.append(NodeTable[i][t - 1] * A[i][j] * B[j][Object[t]])
            if (mod == "viterbi"):
                NodeTable[j][t], NodePath[j][t] = max(temp)


    if (mod == "viterbi"):
        print (u"viterbi算法结点值记录表：")
        printTable(NodeTable)
        print (u"viterbi算法路径记录表：")
        printTable(NodePath, type="int")
        target = 0
        maxValue = NodeTable[target][T - 1]
        for i in range(1, NumState):
            if NodeTable[i][T - 1] > maxValue:
                target = i
                maxValue = NodeTable[i][T - 1]
        print (u"viterbi算法最终状态：", target + 1, "\n")
        StateSequeues = [0] * T
        StateSequeues[T - 1] = target + 1
        for i in range(1, T):
            StateSequeues[T - i - 1] = NodePath[StateSequeues[T - i] - 1][T - i]
        return StateSequeues

I = forwardV(A1, B1, pi1, Object1, mod="viterbi")
print (u"通过viterbi算法求得最优路径 I=", I, "\n")

运行结果：

九隐马尔可夫模型

一隐马尔可夫模型的基本概念

（1）隐马尔可夫模型的定义

（2）观测序列的生成过程

（3）隐马尔可夫模型的3个基本问题

二概率计算算法

（1）观测序列概率的前向算法

（2）观测序列概率的后向算法

（3）前向算法和后向算法实例

三学习算法

（1）监督学习

（2）非监督学习

四预测算法

猜你喜欢

九 隐马尔可夫模型

一 隐马尔可夫模型的基本概念

（1）隐马尔可夫模型的定义

（2）观测序列的生成过程

（3）隐马尔可夫模型的3个基本问题

二 概率计算算法

（1）观测序列概率的前向算法

（2）观测序列概率的后向算法

（3）前向算法和后向算法实例

三 学习算法

（1）监督学习

（2）非监督学习

四 预测算法

猜你喜欢

九隐马尔可夫模型

一隐马尔可夫模型的基本概念

二概率计算算法

三学习算法

四预测算法