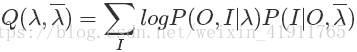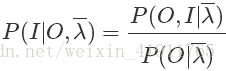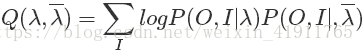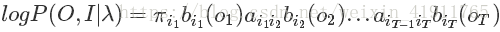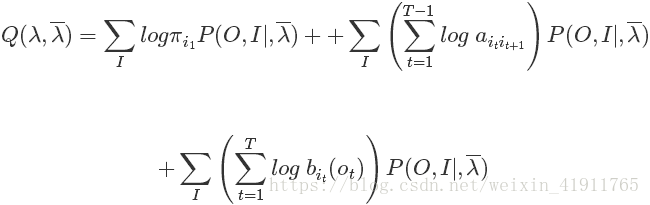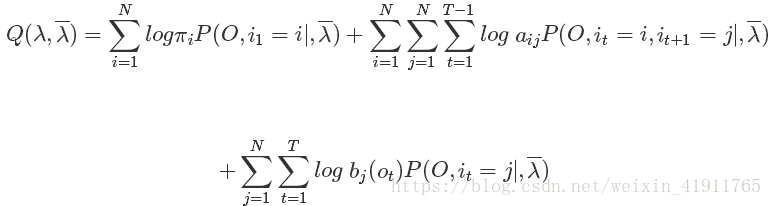HMM隐马尔可夫模型详解

关于什么是隐马尔可夫模型我想你看到的解释应该是酱紫的：

或者是这样子的：

一、什么是隐马尔可夫模型

关于什么是隐马尔可夫模型我想你看到的解释应该是酱紫的：

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，隐马尔科夫模型在语音识别、自然语言处理、生物信息、模式识别等领域有着广泛的应用。

或者是这样子的：

隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观察随机序列的过程......

看不懂没关系，我也看不懂，这可能是出于专业出版的对于定义的严谨性，所以很多时候看不懂一些文献、书籍没关系，我很喜欢博客上各位大神的博文，他们常常能够解决我最根本的问题，看懂了他们博文，再去看书籍和文献，什么都通了。

一、什么是隐马尔可夫模型

我们先用一个例子来说明一下什么是隐马尔可夫模型

该例子来自Yang Eninala博士的知乎https://www.zhihu.com/question/20962240/answer/33438846

一个经典的例子，掷骰子。假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

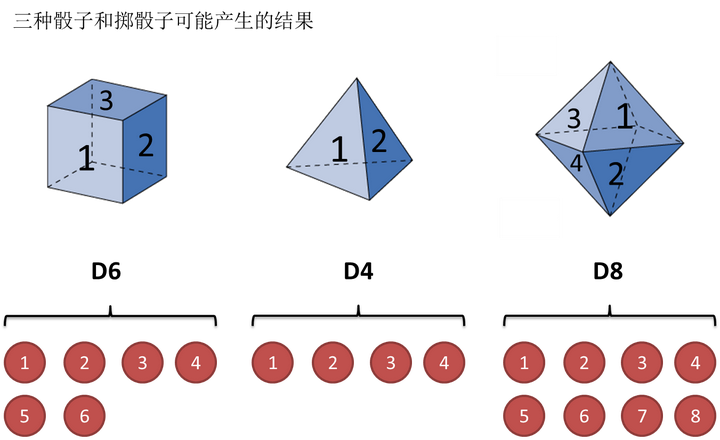
假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4

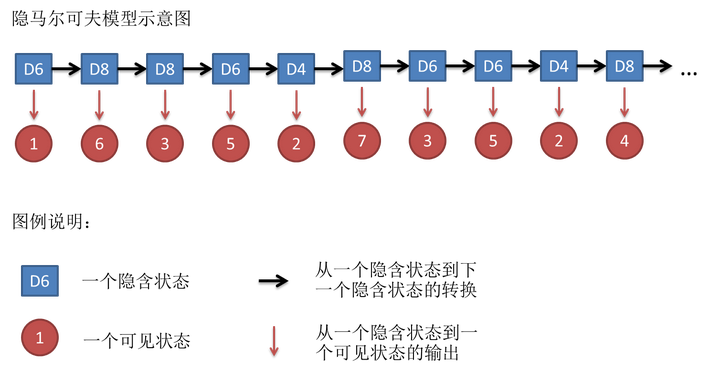
这串数字叫做可见状态链。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8，这条链就是HMM中说到的马尔可夫链。基于这种类型引发的问题就是隐马尔可夫模型。

马尔可夫链不是为了隐马尔科夫模型取的，他的应用也不只是隐马尔可夫。

我们再来看看马尔可夫链的定义过程：

马尔可夫过程的定义：

⑴设是一个随机过程，如果在在时刻所处的状态为已知时，以后的状态与它在时刻之前所处的状态无关，则称具有马尔可夫性。(就是说某个状态的概率只受前一个状态的影响）

⑵设的状态空间为，如果对于任意的，任意的，在条件下，的条件概率分布函数恰好等于其在条件下的条件概率分布函数，即

则称为马尔可夫过程。

((2)在于用公式来表达定义(1)，==》P(t时刻的状态|前1—t-1时刻发生的条件下)=P(t时刻的状态|t-1时刻发生的条件)

其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用HMM模型时候呢，往往是缺失了一部分信息的，有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你只是看到了很多次掷骰子的结果，剩下的什么都不知道。如果应用算法去估计这些缺失的信息，就成了一个很重要的问题。这些东西就是HMM要解决的问题。

二、隐马尔可夫模型要解决的问题

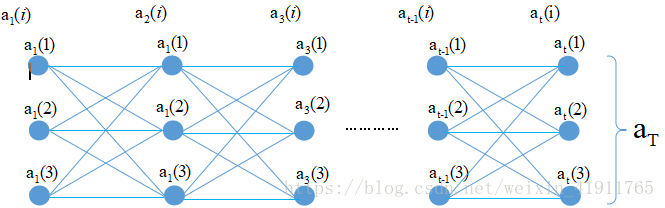
*在提问题之前我们先来定义几个变量(重新看一下这个图的图例)

*几个矩阵的定义

所有可能的状态集合 $Q$ ={ $q_{1},q_{2},q_{3},...,q_{N-1},q_{N}$ }	所有可能的观测集合 $V$ ={ $v_{1},v_{2},v_{3},...,v_{M-1},v_{M}$ }
T时刻的状态序列 $I$ =( $i_{1},i_{2},i_{3},...,i_{t-1},i_{t}$ \| i∈Q)	T时刻的观测序列 $O$ =( $o_{1},o_{2},o_{3},...,o_{t-1},o_{t}$ \| o∈V)
状态转移概率矩阵 $A=[a_{i,j}]_{N*N}$ $a_{i,j}$ 表示t时刻处于状态 $i_{t}=q_{i}$ 转移至 $i_{t+1}=q_{j}$ 的转化概率	观测概率矩阵 $B=[b_{j}(k)]_{N*M}$ $b_{j(k)}$ 表示处于状态 $q_{j}$ 下生成观测 $o_{t}=v_{k}$ 的生成概率
模型参数 λ(A,B,Π)，Π为初始状态概率向量，A为状态转移概率矩阵，B为观测概率矩阵，Π和A决定状态序列，B决定观测序列

*马尔可夫链的两个假设

(1)齐次马尔可夫假设：	即t时刻的状态只受t-1时刻状态的影响
(2)观测独立性假设：	即任意时刻的观测只受该时刻所处状态的影响

*马尔可夫模型的三个基本问题

(1)概率计算问题：	给定模型参数 λ(A,B,Π)和观测序列 $O$ =( $o_{1},o_{2},o_{3},...,o_{t-1},o_{t}$ )，计算在模型λ下观测序列O出现的概率 $P(O\|\lambda)$
(2)学习问题：	给定观测序列 $O$ =( $o_{1},o_{2},o_{3},...,o_{t-1},o_{t}$ )，求参数λ(A,B,Π)，这就是类似EM算法的问题了.
(3)预测问题：	给定参数 λ(A,B,Π)和观测序列 $O$ =( $o_{1},o_{2},o_{3},...,o_{t-1},o_{t}$ )，求隐含的状态序列 $I$ =( $i_{1},i_{2},i_{3},...,i_{t-1},i_{t}$ ).

问题(1)是求条件概率问题。(2)在解决这个问题的时候用的是Baum-welch算法，它是由EM算法引发出来的，而EM算法里面又涉及到极大似然估计的知识，本文会简单的交代一下EM算法，至于极大似然估计的问题如果不懂的话先补完知识再看。往后有时间我会写这个节点的博文。(3)是隐马尔可夫模型的核心，很多领域对隐马尔可夫模型的应用大部分会是问题(3)，比如在机器翻译做中文对英文的翻译时，单词的翻译总是有很多个意思，而词性往往起到很重要的作用，乍一看词性这一序列怎么跟我们说到的隐含的状态序列 $I$ =( $i_{1},i_{2},i_{3},...,i_{t-1},i_{t}$ )很像呢！类似这样的还有很多.......

如果只是想了解一下HMM是什么的话你了解到这里也就差不多了，如果想要知道他长什么样，那就往下。

三、问题解决

1.概率计算问题：

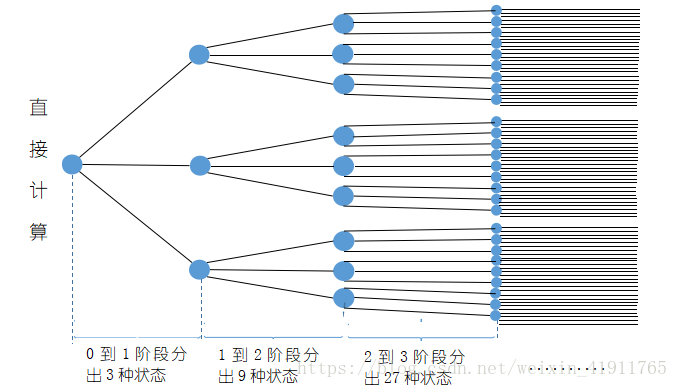
直接计算算法：对所有可能存在的状态序列 $I$ =( $i_{1},i_{2},i_{3},...,i_{t-1},i_{t}$ )，表示出来，形成一个状态序列空间 $D$ { $I_{1},I_{2},I_{3},...,I_{z}$ },并求 $P(O,I|\lambda)$ ，即基于模型 $\lambda$ 求空间D中全部状态序列下出现O的概率。

联合概率 $P(O,I|\lambda)=P(O,|I,\lambda)\cdot P(I|\lambda )$

变成 $\lambda$ 发生的条件下 $I$ 发生的概率 $P(I|\lambda )$ 乘以 $\lambda$ , $I$ 发生的条件下O发生的概率

其中 1) $P(I|\lambda )=\pi _{i}\cdot a_{i_{1},i_{2}}\cdot a_{i_{2},i_{3}}\cdot...\cdot a_{i_{t-1},i_{t}}$ ，

$I$ = $(i_{1},i_{2},i_{3},...,i_{t-1},i_{t})$ , $I\epsilon D$

$D$ 表示所有可能状态序列

2) $P(O,I|\lambda)=b_{i_{1}}(o_{1})\cdot b_{i_{2}}(o_{2})\cdot ...\cdot b_{i_{t}}(o_{t})$

故

$P(O,I|\lambda)=\pi _{i}\cdot b_{i_{1}}(o_{1})\cdot a_{i_{1},i_{2}}\cdot b_{i_{2}}(o_{2})\cdot a_{i_{2},i_{3}}\cdot b_{i_{3}}(o_{3})\cdot...\cdot a_{i_{t-1},i_{t}}\cdot b_{i_{t}}(o_{t})$

对所有满足 $D$ 的 $I$ 求和得到

$P(O|\lambda )=\sum _{I\epsilon D}P(O,I|\lambda )$ $=\sum _{I\epsilon D}\pi _{i}\cdot b_{i_{1}}(o_{1})\cdot a_{i_{1},i_{2}}\cdot b_{i_{2}}(o_{2})\cdot a_{i_{2},i_{3}}\cdot b_{i_{3}}(o_{3})\cdot...\cdot a_{i_{t-1},i_{t}}\cdot b_{i_{t}}(o_{t})$

至此算法结束

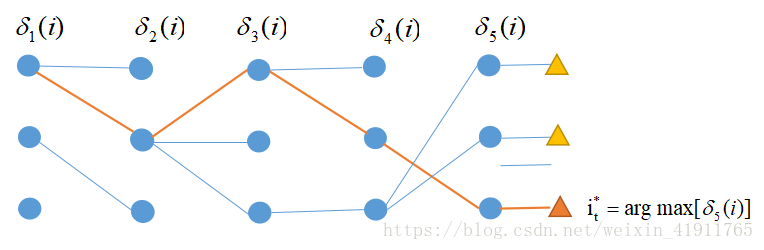
前向算法：直接计算算法很简单便捷，但是计算量很大，假设状态集合 $Q$ 有N个可选的状态，而状态序列 $I$ 有t个节点则可选的状态序列空间 $D$ 就有 $N^{t}$ 个可选序列，这意味这求和项要求和 $N^{t}$ 次，可想而知，计算量不是一般的少。因此引入前向算法：每个节点处先对N个状态分别乘以转化率之后再求和，不理解没关系，先来一幅图。

大概看一下：

定义:

$a_{t}(i)=P(o_{1},o_{2},...,o_{t},i= q_{i} |\lambda )$ ，表示时刻t，其部分观测序列为 $o_{1},o_{2},...,o_{t}$ ，且状态等于 $Q$ 中的 $q_{i}$

故：

(1)初值： $a_{1}(i)=\pi_{i}b_{i}(o_{1}),i\epsilon Q$ 即 $i$ 遍历状态集合

(2)递推 for t =1 to T-1 $a_{t+1}(i)=[ \sum_{j\epsilon Q} a_{t}(j)}\cdot a_{j,i}] b_{i}(o_{t+1}),i\epsilon Q$

即对上一个节点的所以状态乘转化率后求和再乘本节点的生成概率

(3)终止 $P(O|\lambda )=\sum _{I\epsilon Q}a_{T}(i)$ 对最后一节点的所有 $a_{T}(i)$ 求和

后向算法：和前向算法一样，只是顺序倒置了而已,形状参考前向算法，只是对应 $a_t(i)$ 的位置换成 $\beta_t(i)$ 。

定义：

$\beta_t (i)=P(o_{t+1},o_{t+2},...,o_{T}|i_t=q_i,\lambda)$ ，表示 $i_t$ 时刻状态为 $q_i$ 的条件下，往后部分观测序列为 $o_{t+1},o_{t+2},...,o_{T}$ 的概率

(1)初值： $\beta_T(i)=1,i\epsilon Q$

(2)递推 for t=T-1 to 1 $\beta _t(i)=\sum_{j\epsilon D}a_{i,j}\cdot b_j(o_{t+1}) \cdot \beta _{t+1}(j),i\epsilon D$

(3) 终止 $P(O|\lambda )=\sum_{i\epsilon Q}\sum_{j\epsilon Q}\pi_{i}\cdot a_{i,j} \cdot b_j(o_{t+1})\cdot \beta _{t+1}(j)$

至此三个对概率计算的算法算结束了，为了对一下问题(2)和(3)的推导，引入一些概率与期望的计算

一些概率与期望值的计算

1)给定模型 $\lambda$ 和观测序列 $O$ ，在t时刻处于状态 $q_i$ 的概率为：

$\gamma _t(i)=P(i_t=q_i|O,\lambda )=\frac{P(i_t=q_i,O|\lambda )}{P(O|\lambda )}$

由上述前向概率 $a_t(i)$ 和后向概率 $\beta _t(i)$ 的定义可知:

$a_t(i)\cdot \beta _t(i)=P(i_t=q_i,O|\lambda )$

于是得到： $\gamma _t(i)=\frac{a_t(i)\cdot \beta _t(i)}{P(O|\lambda )}=\frac{a_t(i)\cdot \beta _t(i)}{\sum_{j\epsilon Q}a_t(j)\cdot \beta _t(j)}$

2)给定模型 $\lambda$ 和观测序列 $O$ ，在t时刻状态 $q_i$ ，且在t+1时刻处于状态 $q_j$ 的概率为：

$\xi _t(i,j)=P(i_t=q_i,i_{t+1}=q_j|O,\lambda )=\frac{P(i_t=q_i,i_{t+1}=q_j,O|\lambda )}{P(O|\lambda )}$

$\xi _t(i,j)=\frac{a_t(i) a_{ij} b_i(o_{t+1})\beta _{t+1}(j)}{\sum _{i\epsilon D}\sum _{j\epsilon D}a_t(i)a_{ij}b_j(o_{t+1})\beta _{t+1}(j)}$

3)将 $\gamma _t(i)$ 和 $\xi _t(i,j)$ 对各个时刻t求和，可以得到一些有用的期望：

①在观测序列 $O$ 的条件下状态 $i$ 出现的期望值： $\sum_{t=1}^{T}\gamma _t(i)$

②在观测序列 $O$ 的条件下由状态 $i$ 转移的期望值： $\sum_{t=1}^{T-1}\gamma _t(i)$

③在观测序列 $O$ 的条件下由状态 $i$ 转移到状态 $j$ 的期望值： $\sum_{t=1}^{T}\xi _t(i,j)$

注：上面几个应该有错，似乎忽略了各个时刻相交的部分，使得期望变大。

以1为例假如状态集Q有10个状态，时刻T=10，并且各个时刻状态下i出现的概率都是相等的，

则 ${\color{Blue} \gamma _t(i)}$ =0.1， ${\color{Blue}\sum_{t=1}^{T}\gamma _t(i)}$ =1，这是不可能存在的，

应该是 ${\color{Blue} 0.1+(1-0.1)*0.1+(1-0.1)^2*0.1......+(1-0.1)^9*0.1}$ 。

通项就是 ${\color{Blue} 0.1*\sum _{i=1}^{T}(1-0.1)^{T-1}}$

但是 $Q$ 的分布总是乱七八糟的，没办法写出通项来。

2.学习问题：

学习问题就是给定观测序列 $O=(o_{1},o_{2},o_{3},...,o_{t-1},o_{t})$ ，求参数 $\lambda (A,B,\Pi)$ 映射到我们起初提到的骰子的例子大概就是知道了观测序列为 $O=(2,4,8,5,1,3)$ 要求参数

1)A: t时刻选用骰子D4到t+1时刻选用骰子D6或D8的转换概率。

2)B: 任意时刻选用固定骰子后出现某个点数 $v_i$ 的概率。

3)Π: 其实选择骰子D4、D6、D8的概率。

如果知道了隐藏的状态序列 $I$ ，即是每个时刻都选用了哪个骰子的话，求参数 $\lambda (A,B,\Pi)$ 我们直接选用极大似然估计就好了，可是关键在于我们并不知道 $I$ 是什么。因此我们采用Baum-welch算法来求解，而该算法来自与EM算法的变形。

Baum-Welch算法：

是为了解决HMM的参数估计问题而提出的，而且是没有标注也就是HMM的状态序列未知的参数估计问题。具体来说，就是已知观测序列O=(o1,o2,...,oT)O=(o1,o2,...,oT)，估计模型参数λ=(A,B,π)λ=(A,B,π)，使得在该模型下观测序列概率P(O|λ)P(O|λ)最大。由于状态序列未知，因此这可以看做是一个含有隐变量的参数估计问题，解决这一问题的经典算法就是EM算法。Baum-Welch算法就是EM算法在隐马尔科夫模型学习中的具体体现。下面简单叙述一下该算法。

首先按照EM算法，我们需要先写出Q函数。Q函数是完全数据的对数似然函数关于给定模型参数和观测变量的前提下对隐变量的条件概率分布的期望。如下:

我们写出Q函数之后后面就要对它进行极大化，也就是说EM算法的M步骤。既然是最大化，那么只要保证不影响最终的结果，对Q函数进行对于最大化来说没有影响的常数因子乘除是可以的。我们注意到Q函数的后部分

而P(O|λ)P(O|λ)便是概率计算问题中我们解决的问题，对于固定的模型参数来说它是一个常量，因此我们为了后边计算方便可以在上面原先的Q函数的基础上乘以它，使得Q函数成为：

为什么要这么做呢？这是为了后面将概率计算问题中有意义的一些概率计算公式直接套进去。

又因为完全数据可以写成这样：

于是Q函数可以写成：

此时我们看到待估计的参数刚好分别出现在三个项中，所以只需对各个项分别极大化。然后直接极大化我们无法对公式进行细致描述，因此需要将以上Q函数形式修改一下，变成下面这样：

可以看到，我们将三项中分别的对的求和进行了划分。由于隐变量 $I$ =( $i_{1},i_{2},i_{3},...,i_{t-1},i_{t}$ )。原来的求和需要遍历所有 $I$ 的取值，然后进行求和，然而这基本是不可能完成的任务。改写后，我们将遍历的空间进行了划分，同时很好地将 $P(O,I|\bar{\lambda})$ 部分改写后也融入到求和其中。比如第一项，对 $I$ 的遍历等价于先固定状态 $i_1$ ，使其分别取值所有可能的状态（共有N个可取的离散状态），而 $i_2-i_t$ 仍然像原来一样随便取值。这样，就把II空间划分成了N个更小的空间。然后再把这N个空间的结果相加，等价于原来对空间 $I$ 进行遍历。