隐马尔可夫模型：引言

隐马尔可夫模型

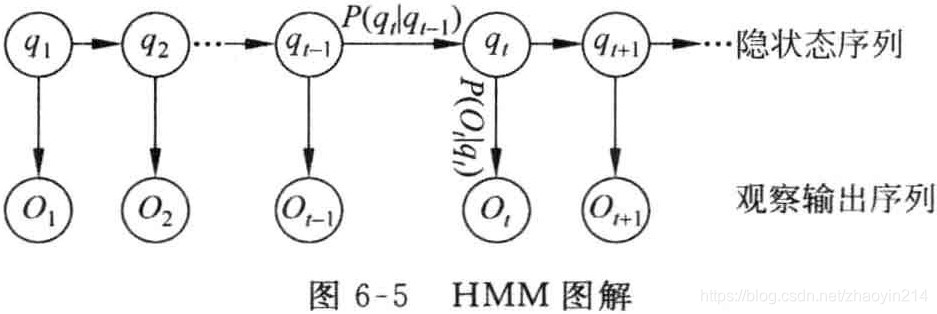
在马尔可夫模型中，每个状态代表了一个可观察的事件，因此，马尔可夫模型又称作可视马尔可夫模型（visible Markov model，VMM）。隐马尔可夫模型（HMM）中，模型所经过的状态序列未知，只知道状态的概率函数，即观察到的事件是状态的随机函数，因此，该模型是一个双重随机过程。其中，模型的状态转换过程是不可观察的（隐蔽的），可观察事件的随机过程是隐蔽状态转换过程的随机函数。

HMM模型可表示为一个五元组 $\mu = (S, K, \mathbf{A}, \mathbf{B}, \mathbf{\pi})$，其中 $S$为状态的集合， $K$为输出符号的集合， $\mathbf{\pi}$、 $\mathbf{A}$和 $\mathbf{B}$分别表示初始状态的概率分布、状态转移概率和符号发射概率。有时也将其简记为三元组 $\mu = (\mathbf{A}, \mathbf{B}, \mathbf{\pi})$。

1. 模型中的状态数 $N = |S|$；

2. 每个状态可能输出的符号数 $M = |K|$；

3. 状态转移概率矩阵 $\mathbf{A} = \{ a_{ij} \}$，其中

$\begin{aligned} & a_{ij} = P(q_{t} = s_{j} | q_{t - 1} = s_{i}) \\ & a_{ij} \geq 0 \\ & \sum_{j = 1}^{N} a_{ij} = 1 \\ & 1 \leq i, j \leq N \\ \end{aligned} \tag {6-6}$

4. 从状态 $s_{j}$观察到符号 $v_{k}$的概率分布矩阵 $\mathbf{B} = \{ b_{j}(k) \}$，其中

$\begin{aligned} & b_{j}(k) = P(O_{t} = v_{k} | q_{t} = s_{j}) \\ & b_{j}(k) \geq 0 \\ & \sum_{k = 1}^{M} b_{j}(k) = 1 \\ & 1 \leq j \leq N, \ 1 \leq k \leq M \\ \end{aligned} \tag {6-7}$

观察符号的概率又称符号发射概率（symbol emission probability）；

5. 初始状态概率分布 $\mathbf{\pi} = \{ \pi_{i} \}$，其中，

$\begin{aligned} & \pi_{i} = P(q_{1} = s_{i}) \\ & \pi_{i} \geq 0 \\ & \sum_{i = 1}^{N} \pi_{i} = 1 \\ & 1 \leq i \leq N \\ \end{aligned} \tag {6-8}$

考虑潜在事件随机地生成表面事件，假设给定HMM模型 $\mu = (\mathbf{A}, \mathbf{B}, \mathbf{\pi})$，则观察序列 $O = O_{1} O_{2} \cdots O_{T}$可以由以下步骤产生：

1. 根据初始状态的概率分布 $\mathbf{\pi}$，选择一个初始状态 $q_{1} = s_{i}$；

2. 设 $t = 1$；

3. 根据状态 $s_{i}$的输出概率分布 $b_{i}(k)$输出 $O_{t} = v_{k}$；

4. 根据状态转移概率分布 $a_{ij}$，将当前时刻 $t$的状态转移到新的状态 $q_{t + 1} = s_{j}$；

5. $t = t + 1$，如果 $t \lt T$，重复执行步骤（3）、（4），否则，结束算法。

HMM的三个基本问题：

1. 估计问题：给定观察序列 $O = O_{1} O_{2} \cdots O_{T}$和模型 $\mu = (\mathbf{A}, \mathbf{B}, \mathbf{\pi})$，计算观察序列 $O$的概率，即 $P( O | \mu)$；

2. 序列问题：给定观察序列 $O = O_{1} O_{2} \cdots O_{T}$和模型 $\mu = (\mathbf{A}, \mathbf{B}, \mathbf{\pi})$，选择在一定意义下“最优”的状态序列 $Q = q_{1} q_{2} \cdots q_{T}$，使得该状态序列“最好地解释”观察序列；

3. 训练问题（参数估计问题）：给定一个观察序列 $O = O_{1} O_{2} \cdots O_{T}$，根据最大似然估计计算模型参数值，即计算使 $P(O | \mu)$最大时，模型 $\mu = (\mathbf{A}, \mathbf{B}, \mathbf{\pi})$的参数。

三个基本问题可通过前后向算法及参数估计解决。