隐马尔可夫模型求解三大问题实例剖析
HMM 模型如图所示:

一、隐马尔可夫模型定义
隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。
设 Q(图中的q)是所有可能的状态的集合,V(图中的O) 是所有可能的观测的集合。
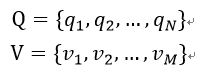
其中,N为可能状态数,M为可能的观测数。
I是长度为T的隐藏状态序列,O是对应的观测序列。
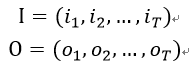
以下三个参数(A、B、π):
A是状态转移概率矩阵:

其中,
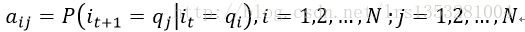
表示在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。
B是观测概率矩阵:

其中,
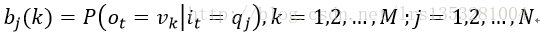
表示在时刻t处于状态qj 的条件下生成观测vk的概率。
π是初始状态概率向量:就是由空状态转换为有状态的一个概率

其中,

表示时刻t=1处于状态qi的概率。
隐马尔可夫模型由π、A、B决定。π和A决定状态序列,B决定观测序列。
隐马尔可夫模型 λ=( A, B,π),A、B、π称为隐马尔科夫模型的三要素。
隐马尔可夫模型的两个基本假设:
(1)齐次马尔可夫性假设
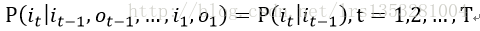
(2)观测独立性假设

二、隐马尔可夫模型的三个基本问题
问题一:概率计算问题:观察序列的概率
给定模型λ=( A, B,π)和观测序列
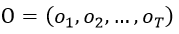
。计算在模型λ下观测序列O出现的概率P(O|λ)。
解决此问题的方法为前向、后向算法。
问题二:预测问题:由观察序列求隐藏序列
比如:HMM 写的拼音输入法
也称为解码问题。已知模型λ=( A, B,π)和观测序列

,求对给定观测序列条件概率P(I|O)最大的状态序列 。即给定观测序列、
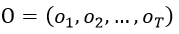
,求最有可能的对应隐藏状态序列
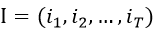
解决此问题的方法为维特比算法。
问题三:学习问题:HMM参数估计
已知观测序列
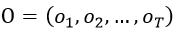
,估计模型λ=( A, B,π)参数,使得在该模型下观测序列概率P(O|λ)最大。
当同时给定观测序列和对应状态序列时,使用极大似然估计方法估计参数。
当只给定观测序列,没有对应状态序列时,基于EM算法进行参数估计。(Baum-Welch算法)
三、隐马尔可夫模型的实例
模型实例
假设 S 是天气状况的集合,分别是“晴天”、"多云"、“下雨”,
其初始概率分布为,
| 晴天 |
多云 |
下雨 |
| 0.63 |
0.17 |
0.20 |
其状态转移概率矩阵为:
| - |
晴 |
阴 |
雨 |
| 晴 |
0.500 |
0.375 |
0.125 |
| 阴 |
0.250 |
0.125 |
0.625 |
| 雨 |
0.250 |
0.375 |
0.325 |
假设有一位盲人住在海边,他不能通过直接观察天气的状态来预报天气。但他有一些水藻,因此可以利用水藻的干湿来预报天气。水藻的干湿与天气状况之间的关系如下表:
| - |
干燥 |
稍干 |
潮湿 |
湿透 |
| 晴 |
0.60 |
0.20 |
0.15 |
0.05 |
| 阴 |
0.25 |
0.25 |
0.25 |
0.25 |
| 雨 |
0.05 |
0.10 |
0.35 |
0.50 |
问题1:求解观察序列的概率
针对上述模型,我们求p(干燥,潮湿,湿透)。思路很简单:
- 确定隐状态的初始概率分布,这是已知的,参见下图第一列。
- 根据隐状态到观测结果“干燥”的发射概率(参见下图第一列到第二列的箭头标注),计算得到“干燥”这个观测结果时,三个隐状态的概率,参见下图第二列。
- 根据隐状态之间的转移概率,重新确定在观测到“干燥”结果后的第二天,隐状态的概率分布,参见下图第三列。图中,我只标注了“晴”的计算过程,其他两天气则省略没画,建议自己亲自计算一下,验证一下。

这个时候再往下计算,方法就和第一步一样了,不再罗嗦了。
问题2:由观察序列确定隐状态序列
例如用HMM 算法来写中文输入法
我们观察到了“干燥、潮湿、湿透”,那么实际天气变化的序列应该是什么呢?会是凭直觉猜测的“晴、阴、雨”这个序列吗?
解决这个问题的关键是,如何计算p(晴阴雨|干燥 潮湿 湿透)?我画了一张图,只要把黑色路径上标注的初始概率、转移概率、发射概率连乘起来,就得到这条路经的概率。

ok,现在问题变成了如何从开始到结束找到一条概率最大的路径。问题转化成了路径最优化问题,可以用动态规划方法解决,我不想再啰嗦了,剩下的任务大家自行解决吧。
问题3:HMM参数估计
假设隐马尔可夫模型的观测序列是“干燥,潮湿,湿透,…”,那么,隐马尔可夫模型的参数A,B,π 如何设置,才能使这个观测序列出现的概率最大?这就是所谓的隐马尔可夫模型参数估计问题。
参照上图,从起点到终点共计27条路径,把这些路径的概率全部加起来,就是“干燥,潮湿,湿透”发生的概率。如果图中箭头随对应的概率全部为未知,可以想想,最终的结果就可以用这些参数表示。因此问题可描述为,这些参数取何值时,所求概率最大。
上图中的实例, 计算观察序列的概率应该不需要遍历27条路径,这样复杂度太高了。这个问题大家自行考虑吧。
转移概率矩阵和发射概率矩阵在多个环节重复出现,让我联想起卷积神经网络的卷积层设计,扯得有点远。但是,这个概率网络求解整体过程的确与神经网络类似。
一个不好的消息是,没办法用公式求解此最优化问题。一个稍好一点的消息是,可以用梯度下降法,求局部极小解,这简直是废话。还有一个稍好点的消息,Baum-Welch算法可以解决此问题,思路类似EM算法,思路也很简单,
Baum-Welch算法
比如,先假设状态序列为已知,参见下表。呵呵,和EM算法套路一样,如果不了解建议看看我写的《简析EM算法(最大期望算法)》。
| t |
观察值 |
晴朗 |
多云 |
下雨 |
| 1 |
干燥 |
1 |
0 |
0 |
| 2 |
潮湿 |
0 |
1 |
0 |
| 3 |
湿透 |
1 |
0 |
0 |
| 4 |
潮湿 |
0 |
0 |
1 |
| 5 |
干燥 |
0 |
1 |
0 |
| 6 |
潮湿 |
1 |
0 |
0 |
| 7 |
湿透 |
0 |
0 |
1 |
| … |
… |
… |
… |
… |
状态的出现次数为0或1,和EM算法是完全一样的套路。如果出现100次"晴朗"
,其中对应70次“干燥”,则可以估计“晴朗”向“干燥”发射概率为70/100=0.7,如此类推,可以求出模型中的所有概率值。
现在的问题是,状态出现的次数是不知道的。依据EM算法思路,可以随机给模型参数赋值(当然要保证数据的合理性)。比如,根据“晴朗”、“阴天”、“下雨”向“干燥”的发射概率,把状态出现次数1按比例分配给三个状态。这样就可以按照上面的方法重新计算模型的参数了。如此类推,直到模型参数收敛为止。
状态转移概率,也可以统计出来。比如从上表1、2两行可以得到“晴天”到“多云”转移累计计数1次。在EM算法中,这个计数可能变成了用小数表示的模糊计数,不过没关系,一样可以得到这个累计计数。
初始概率计算也是同样道理,用模糊计数方法可以帮助估计概率分布。
参考博客和书籍:
https://blog.csdn.net/quicmous/article/details/52208302
https://blog.csdn.net/lrs1353281004/article/details/79417225
《统计学习方法》李航