所谓图像风格迁移,是指利用算法学习著名画作的风格,然后再把这种风格应用到另外一张图片上的技术。著名的图像处理应用Prisma是利用风格迁移技术,普通用户的照片自动变换为具有艺术家风格的图片。
一、图像风格迁移的原理
1、原始图像风格迁移的原理
在学习原始的图像风格迁移之前,可以在先看看ImageNet图像识别模型VGGNet(微调(Fine-tune)原理)。事实上,可以这样理解VGGNet的结构:前面的卷积层是从图像中提取“特征”,而后面的全连接层把图片的“特征”转换为类别概率。其中,VGGNet中的浅层(如conv1_1,conv1_2),提取的特征往往是比较简单的(如检测点、线、亮度),VGGNet中的深层(如conv5_1,conv5_2),提取的特征往往比较复杂(如有无人脸或某种特定物体)。
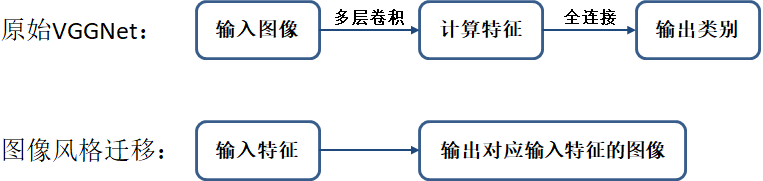
VGGNet本意是输入图像,提取特征,并输出图像类别。图像风格迁移正好与其相反,输入的是特征,输出对应这种特征的图片,如下图所示:
具体来说,风格迁移使用卷积层的中间特征还原出对应这种特征的原始图像。如下图所示,先选取一幅原始图像,经过VGGNet计算后得到各个卷积层的特征。接下来,根据这些卷积层的特征,还原出对应这种特征的原始图像。

下面的a、b、c、d、e分别为使用conv1_2、conv2_2、conv3_2、conv4_2、conv5_2的还原图像。可以发现:浅层的还原效果往往比较好,卷积特征基本保留了所有原始图像中形状、位置、颜色、纹理等信息;深层对应的还原图像丢失了部分颜色和纹理信息,但大体保留原始图像中物体的形状和位置。

还原图像的方法是梯度下降法。设原始图像为$\vec{p}$,期望还原的图像为$\vec{x}$(即自动生成的图像)。使用的卷积是第$l$层,原始图像$\vec{p}$在第$l$层的卷积特征为$P_{ij}^{l}$。$i$表示卷积的第$i$个通道,$j$表示卷积的第$j$个位置。通常卷积的特征是三维的,三维坐标分别对应(高、宽、通道)。此处不考虑具体的高和宽,只考虑位置$j$,相当于把卷积“压扁”了。比如一个10x10x32的卷积特征,对应$1\leqslant i\leqslant 32$,$1\leqslant j\leqslant 100$。对于生成图像$\vec{x}$,同样定义它在$l$层的卷积特征为$F_{ij}^{l}$。
有了上面这些符号后,可以写出“内容损失”(Content Loss)。内容损失$L_{content}(\vec{p},\vec{x},l)$的定义是:
$L_{content}(\vec{p},\vec{x},l)=\frac{1}{2}\sum\limits_{i,j}(F_{ij}^{l}-P_{ij}^{l})^{2}$
$L_{content}(\vec{p},\vec{x},l)$描述了原始图像$\vec{p}$和生成图像$\vec{x}$在内容上的“差异”。内容损失越小,说明它们的内容越接近;内容损失越大,说明它们的内容差距也越大。先使用原始图像$\vec{p}$计算出它的卷积特征$P_{ij}^{l}$,同时随机初始化$\vec{x}$。接着,以内容损失$L_{content}(\vec{p},\vec{x},l)$为优化目标,通过梯度下降法逐步改变$\vec{x}$。经过一定步数后,得到的$\vec{x}$是希望的还原图像了。在这个过程中,内容损失$L_{content}(\vec{p},\vec{x},l)$应该是越来越小的。
除了还原图像原本的“内容”之外,另一方面,还希望还原图像的“风格”。那么,图像的“风格”应该怎么样来表示呢?一种方法是使用图像的卷积层特征的Gram矩阵。
Gram矩阵是关于一组向量的内积的对称矩阵,例如,向量组$\vec{x_{1}}$,$\vec{x_{2}}$,...,$\vec{x_{n}}$的Gram矩阵是
$\begin{bmatrix}
(\vec{x_{1}},\vec{x_{1}}) &(\vec{x_{1}},\vec{x_{2}}) &... &(\vec{x_{1}},\vec{x_{n}}) \\
(\vec{x_{2}},\vec{x_{1}}) & (\vec{x_{2}},\vec{x_{2}}) & ... & (\vec{x_{2}},\vec{x_{n}})\\
...& ...& ...&... \\
(\vec{x_{n}},\vec{x_{1}})& (\vec{x_{n}},\vec{x_{2}}) & ... & (\vec{x_{n}},\vec{x_{n}})
\end{bmatrix}$
通常取内积为欧几里得空间上的标准内积,即$(\vec{x_{i}},\vec{x_{j}}) = \vec{x_{i}}^{T}\vec{x_{j}}$。
设卷积层的输出为$F_{ij}^{l}$,那么这个卷积特征对应的Gram矩阵的第$i$行第$j$个元素定义为
$G_{ij}^{l}=\sum\limits_{k}F_{ik}^{l}F_{jk}^{l}$
设在第$l$层中,卷积特征的通道数为$N_{l}$,卷积的高、宽乘积为$M_{l}$,那么$F_{ij}^{l}$满足$1\leqslant i\leqslant N_{l}$,$1\leqslant j\leqslant M_{l}$。G实际是向量组$F_{1}^{l}$,$F_{2}^{l}$,...,$F_{i}^{l}$,...,$F_{N_{l}}^{l}$的Gram矩阵,其中,其中$F_{i}^{l}=(F_{i1}^{l},F_{i2}^{l},...,F_{ij}^{l},...,F_{iM_{l}}^{l})$。
此处数学符号较多,因此再举一个例子来加深读者对此Gram矩阵的理解。假设某一层输出的卷积特征为10x10x32,即它是一个宽、高均为10,通道数为32的张量。$F_{1}^{l}$表示第一个通道的特征,它是一个100维的向量,$F_{2}^{l}$表示第二个通道的特征,它同样是一个100维的向量,它对应的Gram矩阵G是
$\begin{bmatrix}
(F_{1}^{l})^{T}(F_{1}^{l}) & (F_{1}^{l})^{T}(F_{2}^{l}) & ... &(F_{1}^{l})^{T}(F_{32}^{l}) \\
(F_{2}^{l})^{T}(F_{1}^{l}) & (F_{2}^{l})^{T}(F_{2}^{l}) & ... & (F_{2}^{l})^{T}(F_{32}^{l})\\
...& ... &... &... \\
(F_{32}^{l})^{T}(F_{1}^{l})& (F_{32}^{l})^{T}(F_{2}^{l}) & ... & (F_{32}^{l})^{T}(F_{32}^{l})
\end{bmatrix}$
Gram矩阵可以在一定程度上反映原始图片中的“风格” 。仿照“内容损失”,还可以定义一个“风格损失”(Style Loss)。设原始图像为$\vec{a}$,要还原的风格图像为$\vec{x}$,先计算出原始图像某一次卷积的Gram矩阵为$A^{l}$,要还原的图像$\vec{x}$经过同样的计算得到对应卷积层的Gram矩阵是$G^{l}$,风格损失定义为
$L_{style}(\vec{p},\vec{x},l)=\frac{1}{4N_{l}^{2}M_{l}^{2}}\sum \limits_{i,j}(A_{ij}^{l}-G_{ij}^{l})^{2}$
分母上的$4N_{l}^{2}M_{l}^{2}$是一个归一化项,目的是防止风格损失的数量级相比内容损失过大。在实际应用中,常常利用多层而非一层的风格损失,多层的风格损失是单层风格损失的加权累加,即$L_{style}(\vec{p},\vec{x})=\sum \limits_{i}w_{l}L_{style}(\vec{p},\vec{x},l)$,其中$w_{l}$表示第$l$层权重。
利用风格损失,可以还原出图像的风格了。如下图所示,尝试还原梵高的著名画作《星空》的风格。


其中,图a是由conv1_1的风格损失还原的,图b是由conv1_1,conv2_1两层的风格损失还原的,图c是由conv1_1,conv2_1,conv3_1,图d为conv1_1,conv2_1,conv3_1,conv4_1风格损失还原的。使用浅层还原的“风格图像”的纹理尺度往往比较小,只保留了颜色和局部的纹理(如图a);组合深层、浅层还原出的“风格图像”更加真实且接近原图片(如图e)。
总结一下,到目前为止介绍了两个内容:
(1)利用内容损失还原图像内容。
(2)利用风格损失还原图像风格。
那么,可不可以将内容损失和风格损失结合起来,在还原一张图像的同时还原另一张图像的风格呢?答案是肯定的,这是图像风格迁移的基本算法。
设原始的内容图像为$\vec{p}$,原始的风格图像为$\vec{a}$,待生成的图像为$\vec{x}$。希望$\vec{x}$可以保持内容图像$\vec{p}$的内容,同时具备风格图像$\vec{a}$的风格。因此组合$\vec{p}$的内容损失和$\vec{a}$的风格损失,定义总的损失函数为
$L_{total}(\vec{p},\vec{a},\vec{x})=\alpha L_{content}(\vec{p},\vec{x})+\beta L_{style}(\vec{a},\vec{x})$
$\alpha$,$\beta$是平衡两个损失的超参数。如果$\alpha$偏大,还原的图像会更接近于$\vec{p}$中,如果$\beta$偏大,还原的图像会更接近$\vec{a}$。使用总的损失函数可以组合$\vec{p}$的内容和$\vec{x}$的风格,这实现了图像风格的迁移。部分还原的图像如下图所示

以上是原始的图像风格迁移的基本原理。事实上,原始的图像风格迁移速度非常慢,在CPU上生成一张图片需要数十分钟甚至几个小时,即使在GPU上也需要数分钟才能生成一张较大的图片,这大大的限制了这项技术的使用场景。速度慢的原因在于,要使用总损失$L_{total}(\vec{p},\vec{a},\vec{x})$优化图片$\vec{x}$,这意味着生成一张图片需要几百步梯度下降法的迭代,而每一步的迭代都需要耗费大量的时间。从另一个角度看,优化$\vec{x}$可以看作是一个“训练模型”的过程,以往都是针对模型参数训练,而这里训练的目标是图片$\vec{x}$,而训练模型一般都比执行训练好的模型要慢很多。下面将会讲到快速图像风格迁移,它把原来的“训练”的过程变成了一个“执行”的过程,因此大大加快了生成风格话图片的过程。
二、快速图像风格迁移的原理
原始的图像风格迁移用一个损失$L_{total}(\vec{p},\vec{a},\vec{x})$来衡量$\vec{x}$是否成功组合了$\vec{p}$的内容和$\vec{a}$的风格。然后以$L_{total}(\vec{p},\vec{a},\vec{x})$为目标,用梯度下降法来逐步迭代$\vec{x}$。因为在生成图像的过程中需要逐步对$\vec{x}$做优化,所以速度比较慢。
快速图像风格迁移的方法是:不使用优化的方法来逐步迭代生成$\vec{x}$,而是使用一个神经网络之间生成$\vec{x}$。对应的网络结构如下图所示:

整个系统由两个神经网络组成,它们在图中由两个虚线框分别标出。左边的是图像生成网络,右边是损失网络。损失网络实际上是VGGNet,这与原始的风格迁移是一致的。同原始图像风格迁移一样,利用损失网络来定义内容损失、风格损失。这个损失用来训练图像生成网络。图像生成网络的职责是生成某一种风格的图像,它的输入是一个图像,输出同样是一个图像。由于生成图像只需要在网络中计算一遍,所以速度比原始图像风格迁移提高很多。
同样使用数学符号严格地阐述上面地过程:设输入的图像为$\vec{x}$,经过图像生成网络生成的图像为$\vec{y}$。$\vec{y}$在内容上应该与原始的内容图像$\vec{y}_{c}$接近,因此可以利用损失网络定义内容损失$L_{content}(\vec{y},\vec{y}_{c})$,内容损失使用的是VGG-16中的relu3_3层输出的特征,对应上图中的$l_{feat}^{\phi ,relu3\_3}$。另一方面,我们还希望$\vec{y}$具有目标风格图像$\vec{y}_{s}$的风格,因此又可以定义一个风格损失$L_{total}(\vec{y},\vec{y}_{c},\vec{y}_{s})$。定义风格损失时使用了VGG-16的四个中间层relu1_2,relu2_2,relu3_3,relu4_3,对应图中的$l_{style}^{\phi ,relu1\_2}$、$l_{style}^{\phi ,relu2\_2}$、$l_{style}^{\phi ,relu3\_3}$、$l_{style}^{\phi ,relu4\_3}$。同样组合这两个损失得到一个总损失$L_{total}(\vec{y},\vec{y}_{c},\vec{y}_{s})$。利用总损失可以训练图像生成网络。训练完成后直接使用图像生成网络生成图像。值得一提的是,在整个训练过程中,一般只固定一种风格$\vec{y}_{s}$,而内容图像$\vec{y}_{c}$取和输入$\vec{x}$一样,即$\vec{y}_{s}$=$\vec{x}$。
下面详细的比较原始图像风格迁移与快速图像风格迁移。

这篇博客详细介绍了原始图像风格迁移的基本原理,其中内容损失、风格损失两种损失函数的定义尤为关键。接着还介绍了快速图像风格迁移的原理,以及它和原始图像风格迁移的对比。