机器学习：多分类及多标签分类

多分类及多标签分类

单标签二分类

单标签二分类问题为最为常见的算法，主要指：label的取值只有两种，即每个实例可能的类别只有两种(A or B)；此时的分类算法其实是在构建一个分类的边界将数据划分为两个类别；

常见的二分类算法有：Logistic，SVM，KNN等
\[ y=f(x),y∈\{-1,+1\} \]

单标签多分类

单标签多分类问题，主要指：待预测的label标签只有一个，但是label标签的取值可能有多种情况，即每个实例的可能类别有K种\((t_1,t_2,...,t_k,k \geq 3 )\)；

常见的单标签多分类算法有：Softmax，KNN等
\[ y=f(x),y∈\{t_1,t_2,...,t_k\} \]

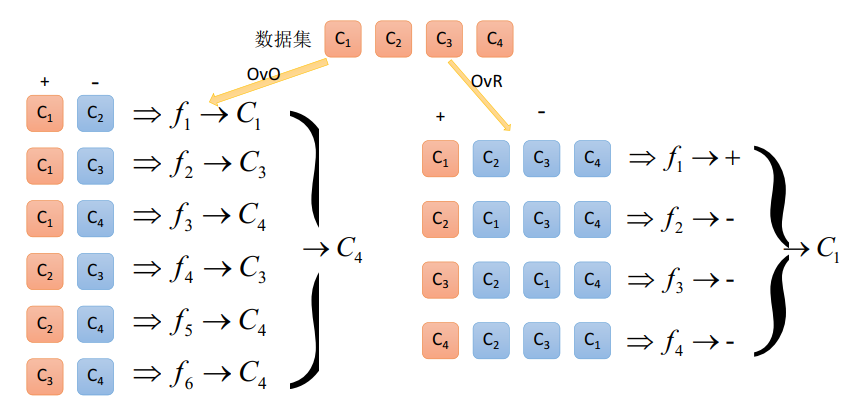
实际上，如一个多分类的问题，可将带求解的多分类的问题转化为二分类问题的延伸；即将多分类任务拆分为若干个二分类任务的求解，具体策略如下：

• OVO(One-Versus-One)：一对一
• OVA/OVR(One-Versus-All/One-Versus-the-Rest)：一对多
• Error Correcting Output Codes(纠错码机制)：多对多

\[ D=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} \]

\[ y_i=j,i=1,2,3,...,m;j=1,2,...,k \]

OVO

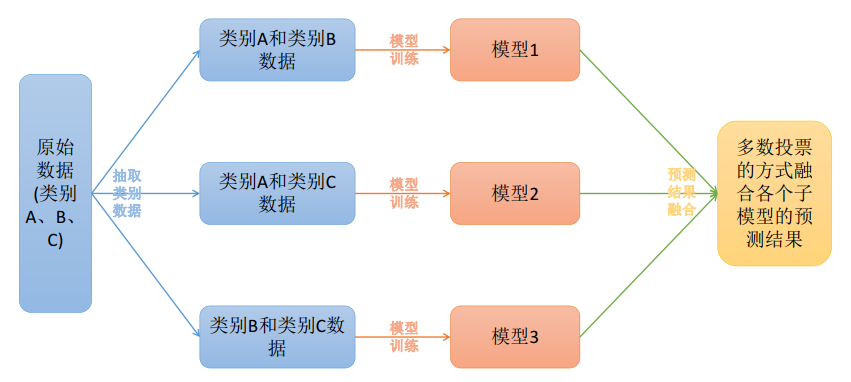
原理：将K个类别中的两两类别数据进行组合，然后使用组合后的数据训练出模型，从而产生\(\frac{K(K-1)}{2}\)个分类器模型，将这些分类器的结果进行融合，并将分类器的预测结果用多数投票的方式输出最终的预测结果值。

eg:

• 若此时有3个类别A,B,C的数据；
• 通过两两组合后，产生AB,AC,BC的数据；
• 采用上述组合后的数据训练出3个模型；
• 对带预测的样本用生成的3个模型采用多数投票的方式进行预测结果。

在生成的模型中还可增加上相应的权重

OVR

原理：在一对多模型训练中，将一个类别作为正例，而其余的样例作为反例来训练K个模型；在进行预测时，若K个模型中，有一个模型输出为正例，那么最终的预测结果就是属于该分类器的这个类别；若产生了多个正例，则可选择分类器的置信度作为指标，选择置信度最大的分类器作为最终的预测结果，常见的置信度有：精确度，召回率。

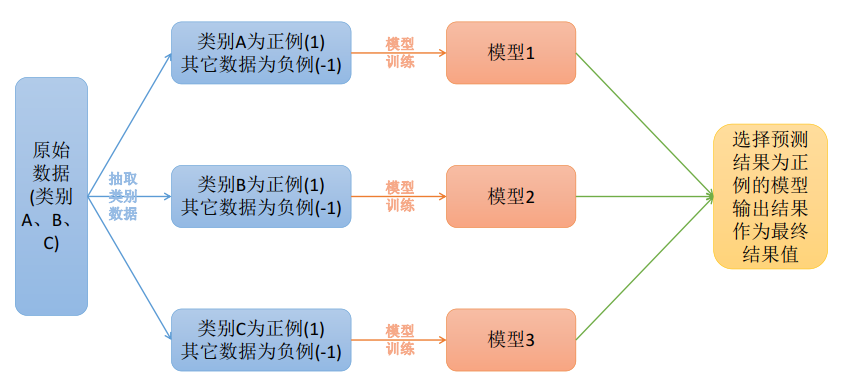
OVO和OVR的区别：

纠错码机制

原理：将模型构建应用分为两个阶段：编码和解码阶段；

• 编码阶段：对K个类别中进行M此划分，每次划分将一部分数据分为正类，一部分数据分为反类，每次划分都构建出一个模型，模型的结果是在空间中对于每个类别都定义了一个点；
• 解码阶段：使用训练出来的模型对测试样例进行预测，将待预测的样本也定义为空间中的一个点，计算该待测点与类别之间的点的距离，选择距离最近的类别作为最终的预测类别。

多标签

Multi-Lable Machine Learning(MLL)，是指预测模型中存在多个y值，具体分为两类不同的情况：

1. 多个预测y值；
2. 在分类模型中，一个样例可能存在多个不固定的类别。

根据多标签问题的复杂性，可以将问题分为两大类：

1. 待预测值之间存在相互的依赖关系；
2. 待预测值之间不存在依赖关系。

x_1	x_2	x_2	x_2	y_1	y_2
1.1	1.5	1.8	1.2	1	1.5
2.1	2.8	2.4	2.4	2.1	2.45
-1.2	-0.5	0.25	-0.12	-0.5	-1
0	0.2	0.89	1.2	0	0.5

x_1	x_2	x_2	x_2	y_1
1.1	1.5	1.8	1.2	a
2.1	2.8	2.4	2.4	b,c
-1.2	-0.5	0.25	-0.12	a,c
0	0.2	0.89	1.2	e

策略转换

Problem Transformation Methods，策略转换，问题转换，是一种将多标签分类问题转换为单标签模型构造的问题，然后将模型合并的一种方式，可分为：

• Binary Relevance(first-order)：标签之间无关联
• Classifier Chains(high-order)：标签之间有依赖关系
• Calibrated Label Ranking(second-order)：两两标签之间有关系

Binary Relevance

Binary Relevance的核心思想是将多标签分类问题进行分解，将其转化为q个二元分类问题，其中每个二元分类器对应一个待预测的标签。

q:标签的数目，即有多少个y；

例如上方表一中的有两个y，\(y_1和y_2\)，用x和\(y_1\)训练一个模型；用用x和\(y_2\)再训练一个模型

\[ D_j=\{ (x_i,Φ(Y_i,y_j))| 1 \leq i \leq m\},其中Φ(Y_i,y_j)=\begin{cases} +1，y_j∈Y_i\\ -1， otherwise \end{cases} \]

\[ i:样本数量;Y_i:第i个样本的标签序列;y_j:第j个标签;D_j:表示x是否属于y_j，属于则为+1，否则为-1 \]

\[ g_j=f(D_j) \]

\[ eg:g_1(x)=1,g_2(x)=-1,g_3(x)=1;表示此事Y=[y_1,y_2,y_3]=\left[ \begin{matrix} 1 & 0 & 1 \end{matrix} \right] \]

\[ Y=\{ y_i | g_j(x) > 0, 1 \leq j \leq q \} ∪ \{ y_{j^*}|j^*=argmax_{1 \leq j \leq q} g_j(x) \} \]

\[ 其中，若存在所有的g_j(x) < 0，因此加上\{ y_{j^*}|j^*=argmax_{1 \leq j \leq q} g_j(x) \}以保证Y不为空 \]

优点：

• 实现方式简单，容易理解；
• 当y值之间不存在相互的依赖关系的时候，模型的效果不错

缺点：

• 如果y之间存在相互的依赖关系，那么最终构建的模型的泛华能力比较弱；
• 需要构建q个二分类器，q为待预测的y值数量，当q较大时，需要构建的模型就相应的较多。

Classifier Chains

Classfier Chains核心思想是将多标签分类问题进行分解，将其转换成一个二元分类器链的形式，其中链后的二元分类器的构建是在前面分类器预测结果的基础上进行的；

在模型构建的时候，首先将标签顺序进行打乱排序操作，然后按照从头到尾构建每个标签对应的模型。

\[ eg：X，Y=[y_1,y_2,y_3,y_4,y_5] \]

\[ shuffle:X，Y=[y_2,y_4,y_1,y_5,y_3] \]

\[ 然后，用X+y_2构建一个预测模型，构建完成后再用X+y_2+y_4构建下一个模型，... \]

\[ τ：shuffle\_sorted\{1,2,...,q\}，对q个划分类别进行打乱 \]

\[ D_{τ(j)}=\{([x_i,pre^i_{τ(j)}],Φ(Y_i,y_{τ(j)}))|1 \leq i \leq m\} \]

\[ pre^i_{τ(j)}=(Φ(Y_i,y_{τ(1)}), Φ(Y_i,y_{τ(2)}),...,Φ(Y_i,y_{τ(j-1)}))^T \]

\[ Φ(Y_i,y_{τ(j)}):打乱后的第j个类别是否在Y_i中存在，若存在为+1，否则为-1 \]

\[ 注：其中pre^i_{τ(1)}为空，因为第一个类别不依赖于任何其他的y值 \]

\[ g_{τ(j)}=f(D_{τ(j)}) \]

\[ λ^x_{τ(1)}=sign(g_{τ(1)}(x)) \]

\[ λ^x_{τ(j)}=sign(g_{τ(j)}([x,λ^x_{τ(1)},λ^x_{τ(2)},...,λ^x_{τ(j-1)}])),2 \leq j \leq q \]

\[ Y=\{y_{τ(j)}|λ^x_{τ(j)}=\pm1,1 \leq j \leq q\} \]

优点：

• 考虑标签之间的依赖关系，最终模型的泛华能力相对于Binary Relevance方式构建的模型效果要好；

缺点：

• 很难找到一个比较合适的标签之间的依赖关系

Calibrated Label Ranking

其核心思想是将多标签分类问题进行分解，将其转换为标签的排序问题，最终的标签就是排序后最大的几个标签值。
\[ D_{jk}=\{ (x_i,l(Y_i,y_j,y_k)) | Φ(Y_i,y_j) \neq Φ(Y_i,y_k), 1 \leq i \leq m \} \]

若有q个类型的标签，则可构建\(\frac{q(q-1)}{2}\)个模型

\[ l(Y_i,y_j,y_k)=\begin{cases} +1，if \space\space Φ(Y_i,y_j)=+1 \space and \space Φ(Y_i,y_k)=-1 \\ -1， if \space\space Φ(Y_i,y_j)=-1 \space and \space Φ(Y_i,y_k)=+1 \end{cases} \]

\[ 由g_{jk}=f(D_{jk})，得 \hat{y}=y_j \space\space if \space g_{jk}(x)>0 \space else \space y_k \]

\[ ζ(x,y_j)=\sum_{k=1}^{j-1}{||g_{jk}(x) \leq 0||} + \sum_{k=j+1}^{q}{||g_{jk}(x) > 0||} \]

和j相关的模型有k-1个，用这k-1个模型对任意样本x进行预测，判断x样本是否属于j类别，而从下方公式看出，j可取多个值，即多标签

\[ Y=\{y_j|ζ(x,y_j)>threshold,1 \leq j \leq q\} \]

上述体现了OVO的思想

但是存在了一个threshold，需要给定，出于给定的困难，故引出下述内容

\[ D_{jV}=\{(x_i,Φ(Y_i,y_j))|1 \leq i \leq m \} \]

\[ 构建模型g_{jV}=f(D_{jV})，得 \hat{y}=y_j \space\space if \space g_{jV}(x)>0 \]

上述体现了OVR的思想

再将OVO和OVR的思想进行结合，引出下述内容

\[ ζ^*(x,y_j)=ζ(x,y_j)+||g_{jV}(x)>0|| \space\space\space\space\spaceζ^*(x)=\sum_{j=1}^{q}{||g_{jV}(x)\leq0||} \]

\(ζ^*(x)\)用于判断x样本是否不属于j类别，两个极端情况：若不属于任何类别，则结果为q；若属于所有类别，则结果为0。用该值来取代了上述threshold，值越大表示样本x越难判断，越小表示样本x越容易判断类别，引出最终的分类结果如下：

\[ Y=\{y_j|ζ^*(x,y_j)>ζ^*(x),1 \leq j \leq q\} \]

优点：

• 考虑了标签两两组合的情况，最终的模型相对来讲泛化能力比较好

缺点：

• 只考虑了两两标签的组合情况， 没有考虑到标签与标签之间所有的依赖关系

Algorithm Adaptation

Algorithm Adaptation，算法适应性策略，一种将现有的单标签算法直接应用到多标签上的一种方式，主要有：

• Multi Label-KNN
• Multi Label-DT

ML-KNN

对于每一个实例而言，先获取距离它最近的K个实例，然后使用这些实例的标签集合，通过最大后验概率(MAP)来判断这个实例的预测标签集合的值。

最大后验概率(MAP)：在最大似然估计(MLE)中加入了这个要估计量的先验概率分布
\[ \hatθ_{MLE}(x)=argmax_θf(x|θ) \]

\[ \hat{θ}_{MAP}(x)=argmax_θ\frac{f(x|θ)g(θ)}{\int_{θ}{f(x|θ^{'})g(θ^{'})}dθ^{'}}=argmax_θf(x|θ)g(θ) \]

\[ C_j=\sum_{(x^*,Y^*)∈N(x)}{||y_j∈Y^*||} \]

\[ N(x):样本x的k近邻;(x^*,Y^*):属于样本x的k近邻的实例;C_j:表示第j个标签在x的K个邻居中间出现的次数 \]

\[ Y=\{ y_j|\frac{P(H_j|C_j)}{P(!H_j|C_j)} > 1, 1 \leq j \leq q\} \]

\[ H_j=1,!H_j=0;P(H_j|C_j)表示在C_j的条件下，属于y_j的概率;上述Y表示了，属于y_j的概率值要大于不属于y_j的概率值 \]

\[ 由贝叶斯公式：\frac{P(H_j|C_j)}{P(!H_j|C_j)}=\frac{\frac{P(C_j|H_j)P(H_j)}{P(C_j)}}{\frac{P(C_j|!H_j)P(!H_j)}{P(C_j)}}=\frac{P(C_j|H_j)P(H_j)}{P(C_j|!H_j)P(!H_j)} \]

\[ 其中P(H_j)=\frac{1}{n}\sum_{i=1}^{n}{y_j∈Y_i}~~~~~~~~~~P(!H_j)=1-P(H_j) \]

\[ P(C_j|H_j)=\frac{k_j[C_j]}{\sum_{r=0}^{K}{k_j[r]}}~~~~~~~~~~P(C_j|!H_j)=\frac{!k_j[C_j]}{\sum_{r=0}^{K}{!k_j[r]}} \]

\[ 其中：k_j[r]=\sum_{i=1}^{n}{||y_j∈Y_i|| \cdot||C_j=r||},0\leq r \leq k~~~~~~~~~~!k_j[r]=\sum_{i=1}^{n}{||y_j∉Y_i|| \cdot||C_j=r||},0\leq r \leq k \]

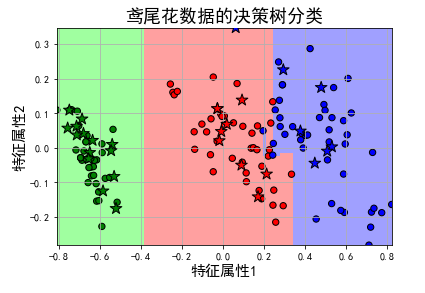
ML-DT

ML-DT使用决策树处理多标签内容，核心在于给予更细粒度的信息熵增益准则来构建这个决策树模型。
\[ entry=\sum_{j=1}^{q}{[-p_jlog_2p_j-(1-p_j)log(1-p_j)]} \]

\[ 其中p_j=\frac{\sum_{i=1}^{n}{||y_i∈Y_i||}}{n} \]

\[ p_j表示在n条样本中，有几条样本包含y_j这个标签值 \]

同样目的也是使得entry信息熵足够的小。

实际应用

• 01_OvO案例代码
• 02_OvR案例代码
• 03_Error-Correcting案例代码
• 04_多标签分类问题
• 05_宫颈癌预测(属于直接使用RF模型训练预测多个y值的情况).ipynb

GitHub