关于主成分分析的理论推导(PCA降维算法)
一 特征选择与特征提取
关于主成分分析,严格一点说,它应该属于特征提取,而不是特征选择。
我们先来看看什么是特征选择?
比如现在我们的训练数据集是:
\[ \left \{ (x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3}),...(x_{p},y_{p}) \right \} \]
其中 :
\[ x_{i} = [ x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} ]^{T} \]
即\(x_{i}\)是一个n维的列向量。
那么特征选择的问题是什么呢?
问:这n个维度有冗余,即\(x_{i}\) 的某些维度对于所研究问题无作用,那么如何从这n个维度中选出最有用的 m(m<n)个特征?
这是特征选择的问题。无论怎样,最后出来的特征,也只是原来特征中挑选出来的,没有出现新增加的特征。
那么特征提取的问题是什么呢?
n个维度\([x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} ]\),构造:
\[ \left \{ f_{1}( x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} ), f_{2}( x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} ), f_{3}( x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} ), ..., f_{m}( x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} ) \right \} \]
即:构造\(\left ( f_{1},f_{2},f_{3},..f_{m} \right )\),以每一个\(f\)来映射\([x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} ]\),从而得到m个\(f_{i}( x_{i1} ,x_{i2} ,x_{i3} ,...x_{in} )\),如果这里的m<n,那么同样达到降维的目的,这种方式称为特征提取,最后产生的每一个特征都是全新的。
那么明确一点,主成分分析(PCA)是属于特征提取。
二 主成分分析的理论推导
第一个主成分的推导
主成分分析的思想其实很简单,困难在于理论证明。本质上主成分分析就是矩阵相乘的本质,矩阵相乘的本质就是把右边矩阵的每一列投影到以左边矩阵每一行为基组的新的矩阵空间当中,如果左边矩阵的行数小于右边矩阵的行数,那么以行来看就会实现降维。举个列子:
\[ A_{3\times 5}\times B_{5\times 8}=C_{3\times 8} \]
这样简单看\(B\)矩阵以行来看,就从5维降成了3维。ok,有了这个了解,我们再来看看主成分分析。
主成分分析在做这些事:构造\(A_{m\times n},b_{m\times 1}\),使\(Y_{m\times 1}=A_{m\times n}X_{n\times 1}+b_{m\times 1}\),m<n
这样,我们就把\(X_{n\times 1}\)降维成了\(Y_{m\times 1}\)。
看起来还是很简单是吧,随便找个满足上面降维的\((A\ b)\)就行了,但是我们不禁思考一个问题,我们这样利用一个矩阵降维,会不会损失\(X\)所含有的信息呢?
答案是一定的,降维几乎肯定是会损失信息,所以我们肯定不能随便找组\((A\ b)\),我们需要的是降维后尽可能的保留\(X\)所含有的全部信息。但是问题来啦:
1、\(X\)的信息在哪里?
2、用什么来衡量?
3、如何找到能保留最多信息的\((A\ b)\)?
其实在统计学里面 ,一个分布的主要信息是方差或者标准差来衡量的,所以主成分分析要做的就是:
找到使投影后方差最大的方向,并向这个方向投影
举个例子:
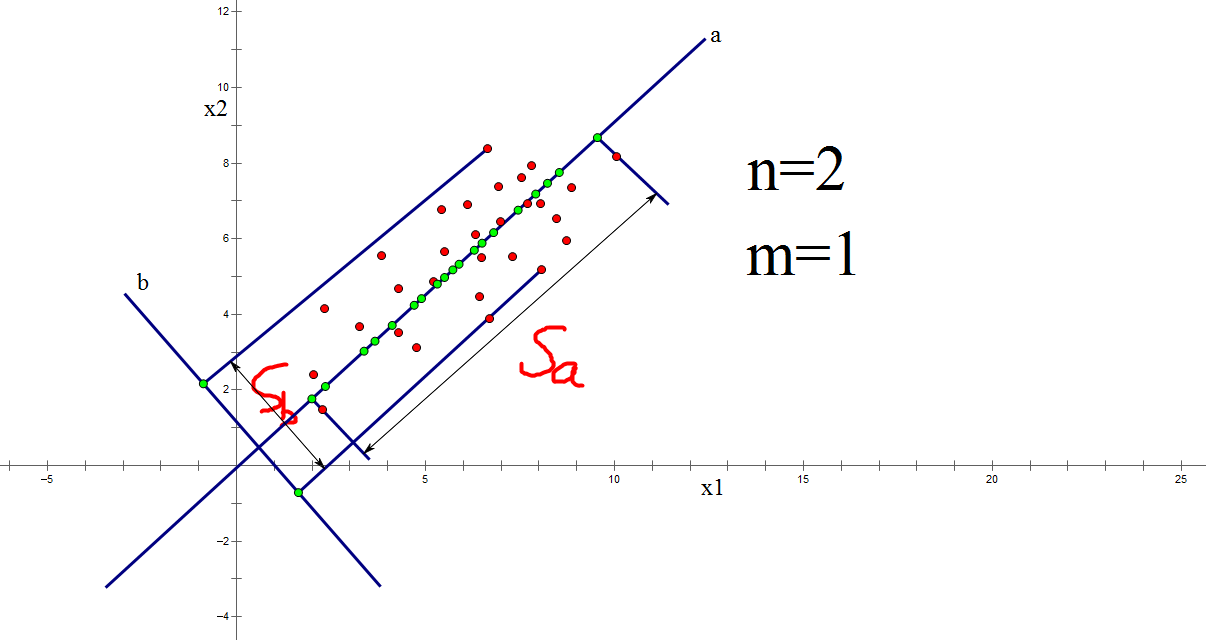
每个红色点代表一个样本\(x_{i}\),\(x_{i}=[x_{i1},x_{i2}]^{T}\)
即,每个样本\(x_{i}\)是两个维度,那么如果要降维的话,只能降成1维。我这里给出了两个投影方向,a b ,在a方向上画出了投影后的绿色点。那么主成分分析认为往a方向上投影更好。原因你可以这样认为,如果投影后的点越分散就越不容易出现重合点,重合的话一定造成信息完全损失。我们把往a投影后得到的称为第一个主成分,往b投影后得到的称为第二个主成分。而如何衡量‘分散’呢?就是方差!所以投影后的数据方差越大,那么含有的信息就越多,损失的信息就越少。
ok,那我们来找最好的\((A\ b)\),但是呢,我们这里先改写一下:
\[ Y_{m\times 1}=A_{m\times n}(X_{n\times 1}-\overline{X_{n\times 1}}) \]
这样只是把\(b_{m\times 1}\)变成了\(-A_{m\times n}\overline{X_{n\times 1}}\),只需要去求\(A_{m\times n}\)
首先呢,我们把\(A_{m\times n}\)写出行向量的形式:
\[ A_{m\times n}=\begin{bmatrix} a_{1}\\ a_{2}\\ ...\\ a_{m} \end{bmatrix} \]
其中\(a_{i}=[a_{i1},a_{i2},a_{i3},...,a_{in}]\),每一个\(a_{i}\)表示一个投影方向。
此时:
\[ Y_{m\times 1}= \begin{bmatrix} a_{1}\\ a_{2}\\ ...\\ a_{m} \end{bmatrix}_{m\times n} \times (X_{n\times 1}-\overline{X_{n\times 1}}) = \begin{bmatrix} a_{1}(X_{n\times 1}-\overline{X_{n\times 1}})\\ a_{2}(X_{n\times 1}-\overline{X_{n\times 1}})\\ ...\\ a_{m}(X_{n\times 1}-\overline{X_{n\times 1}}) \end{bmatrix} \]
这里我们假设一共有\(p\)个\(X\),即:\(\left \{ X_{i} \right \}_{i=1\sim p}\)
那么同样有:
\[ \left \{ Y_{i} \right \}_{m\times 1} = \begin{bmatrix} a_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})\\ a_{2}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})\\ ...\\ a_{m}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})) \end{bmatrix} ,i=1\sim p \]
同样的,这里我们把上式写成行向量的形式:
\[ \left \{ Y_{i} \right \}_{m\times 1} = \begin{bmatrix} y_{i1}\\ y_{i2}\\ ...\\ y_{im} \end{bmatrix} ,i=1\sim p \]
那么现在呢,我们来回顾一下前面说的东西,每一个\(a_{i}\)代表着一个投影方向。
那么既然:\(y_{i1}=a_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})\)
那么\(y_{i1}\)就代表着在第一个方向\(a_{1}\)上投影后的结果,称之为第一个主成分,我们需要的是投影后的结果的方差最大,即:
\[ max:\sum_{i=1}^{p}(y_{i1}-\overline{y}_{i1})^2 \]
那么我们先来计算一下 \(\overline{y}_{i1}\)
\[ \overline{y}_{i1}=\frac{1}{p}\sum_{i=1}^py_{i1} =\frac{1}{p}\sum_{i=1}^pa_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}}) =\frac{a_{1}}{p}[(\sum_{i=1}^p\left \{ X_{i} \right \}_{n\times 1})-p\overline{X_{n\times 1}}] \]
而
\[ p\overline{X_{n\times 1}}=p*\frac{1}{p}\sum_{i=1}^p\left \{ X_{i} \right \}_{n\times 1} =\sum_{i=1}^p\left \{ X_{i} \right \}_{n\times 1} \]
所以
\[ \overline{y}_{i1}=\frac{1}{p}\sum_{i=1}^py_{i1} =\frac{1}{p}\sum_{i=1}^pa_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}}) =\frac{a_{1}}{p}[(\sum_{i=1}^p\left \{ X_{i} \right \}_{n\times 1})-p\overline{X_{n\times 1}}]=0 \]
问题转化为:
\[ max:\sum_{i=1}^{p}y_{i1}^2=[a_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})]^2 \]
这里说明一下,\(a_{1}=(a_{11},a_{12},a_{13},...a_{1n})\),所以\(a_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})\)是一个常数!
所以可以上式可以继续改写:(一个常数的转置就等于本身,下面把右边那个因式转置一下)
\[ max:\sum_{i=1}^{p}y_{i1}^2=\sum_{i=1}^{p}a_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})*[a_{1}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})]^{T} \]
又根据 \((AB)^{T}=B^TA^T\), 把右边的转置因式展开:
\[ max:a_{1}[\sum_{i=1}^{p}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}}) (\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})^{T}]a_{1}^{T} \]
这整个式子最后的结果是一个常数!看下图:
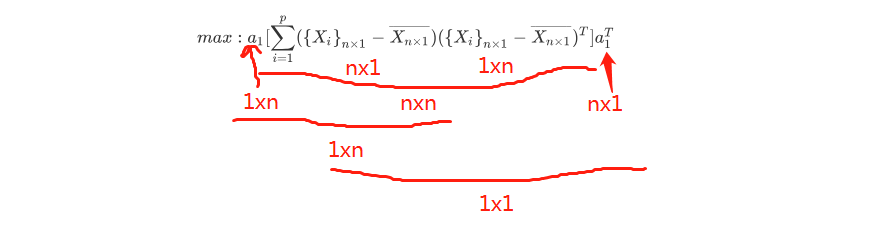
ok,那么现在呢,我们用一个符号来代替中间那一部分!如下式:
\[ [\sum_{i=1}^{p}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}}) (\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})^{T}]=\Sigma \]
上面这个式子在统计学中就叫协方差矩阵( covariance matrix)
这里再来补充一个知识点:\((A+B)^{T}=A^{T}+B^{T}\)
那么来看看下面这个计算:
\[ \Sigma^{T}=[\sum_{i=1}^{p}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})(\left \{ X_{i} \right\}_{n\times 1}-\overline{X_{n\times 1}})^{T}]^{T}=\\ [\sum_{i=1}^{p}(\left \{ X_{i} \right \}_{n\times 1}-\overline{X_{n\times 1}})(\left \{ X_{i}\right\}_{n\times 1}-\overline{X_{n\times 1}})^{T}]=\Sigma \]
这个我们下面会用到。
按理说这里我们的优化问题已经求出来了,协方差矩阵是已经知道的,求\(a_{1}\),但是我们必须再对\(a_{i}\)进行一定的限制,为什么呢?我们说了这里\(a_{i}\)是一个投影的方向,在数学的表达里就是一个多维的向量,一个向量具有方向和模长。而我们主要关注的是方向,必须保证模长一定,所以我们必须对\(a_{i}\)进行一些归一化限制。
于是我们给出下面完整的优化问题:
\[ 最大化:a_{1}\Sigma a_{1}^{T}\\ 限制条件:a_{1}a_{1}^{T}=\left | a_{1} \right |^{2}=1 \]
要解此优化问题要用到拉格朗日乘子法:
不了解的课参考下这篇文章看下:https://zhuanlan.zhihu.com/p/38625079
拉格朗日变换如下:
\[ F(a_{1})=a_{1}\Sigma a_{1}^{T}-\lambda (a_{1}a_{1}^{T}-1) \]
对\(a_{1}\)求导:先给出一些求导的结果,矩阵求导比较陌生,不清楚的网上查一查。
\(\frac{\mathrm{d} (a_{1}\Sigma a_{1}^{T})}{\mathrm{d} a_{1}}=2(\Sigma a_{1}^{T})^{T},\ \ \ \frac{\mathrm{d} (a_{1}a_{1}^{T})}{\mathrm{d} a_{1}}=2a_{1}\)
所以求导后的结果是:
\[ \frac{\partial F}{\partial a_{1}}=2(\Sigma a_{1}^{T})^{T}-2\lambda a_{1} \]
令其等于0:
\[ 2(\Sigma a_{1}^{T})^{T}-2\lambda a_{1}=0\\ \Rightarrow (\Sigma a_{1}^{T})^{T}=\lambda a_{1} \]
上式两边再同时转置:注意\(\lambda\)是一个常数!
\[ \Sigma a_{1}^{T}=(\lambda a_{1})^{T}=\lambda a_{1}^{T} \]
根据特征值与特征向量的定义,上式中:重点来了!
\(a_{1}^{T}\)是协方差矩阵\(\Sigma\)的特征向量,\(\lambda\)是其对应的特征值!
我们要最大化 \(a_{1}\Sigma a_{1}^{T}\\\),可作如下变换:
\[ a_{1}\Sigma a_{1}^{T}=a_{1}(\Sigma a_{1}^{T})=a_{1}\lambda a_{1}^{T}=\lambda(a_{1}a_{1}^{T})=\lambda \]
那么到此我们可以得出结论,我们要想最大化\(a_{1}\Sigma a_{1}^{T}\),就要最大化\(\lambda\)。而\(\lambda\)就是协方差矩阵\(\Sigma\)最大的特征值,此时所求的\(a_{1}\)就是最大特征值所对应的特征向量。
此时求得的\(a_{1}\)就是使得方差最大化的方向,这时得到的第一个主成分就保留了最多的信息。
第二个主成分的推导
我们开始来求第二个主成分,也就是要求\(a_{2}\),但是\(a_{2}\)的限制条件除了归一化限制以外,还要求\(a_{2}\)与\(a_{1}\)保持正定,你也可以认为是垂直。
所以其完整优化问题就是如下:
\[ 最大化:a_{2}\Sigma a_{2}^{T}\\ 限制条件:a_{2}a_{2}^{T}=\left | a_{2} \right |^{2}=1\\ a_{2}a_{1}^{T}=a_{1}a_{2}^{T}=0 (a_{1} , a_{2}要正定) \]
构造拉格朗日函数如下:
\[ F(a_{2})=a_{2}\Sigma a_{2}^{T}-\lambda (a_{2}a_{2}^{T}-1)-\beta a_{2}a_{1}^{T} \]
其中:\(\frac{\mathrm{d} (a_{2}a_{1}^{T})}{\mathrm{d} a_{2}}=a_{1}\)
则原式对\(a_{2}\)求导结果如下:
\[ \frac{\mathrm{d} F}{\mathrm{d} a_{2}}=2(\Sigma a_{2}^{T})^{T}-2\lambda a_{2}-\beta a_{1} \]
令上式等于0:
\[ 2(\Sigma a_{2}^{T})^{T}-2\lambda a_{2}-\beta a_{1}=2a_{2}\Sigma ^{T}-2\lambda a_{2}-\beta a_{1}=0 \]
现在需要先证明\(\beta\)=0
这里要用到我们前面所说的:\(\Sigma\)=\(\Sigma^{T}\),带入上面的第二个等式,得到:
\[ 2a_{2}\Sigma -2\lambda a_{2}-\beta a_{1}=0 \]
我们看看这个式子的结构:
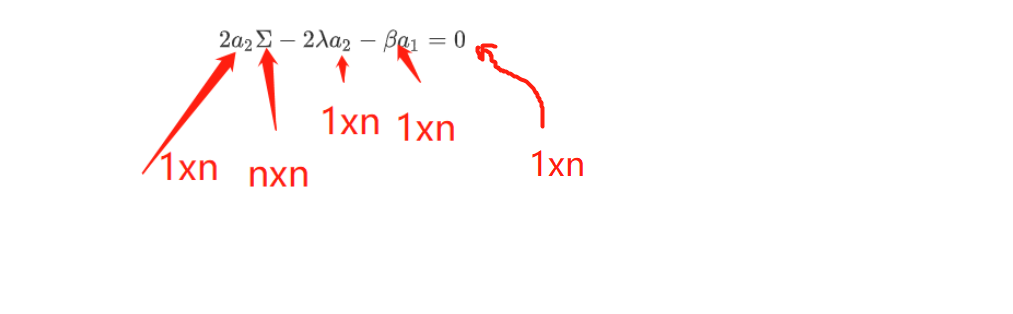
现在上式两边同时乘以\(a_{1}^{T}\):
\[ (2a_{2}\Sigma -2\lambda a_{2}-\beta a_{1})a_{1}^{T}=0,这里0是一个常数! \]

化简:
\[ (2a_{2}\Sigma-2\lambda a_{2}-\beta a_{1})a_{1}^{T}=0\\ \Rightarrow 2a_{2}\Sigma a_{1}^{T}-2\lambda a_{2}a_{1}^{T}-\beta a_{1}a_{1}^{T}=0\\ \Rightarrow 2a_{2}\lambda_{1}a_{1}^{T}-\beta =0\\ \Rightarrow \beta=2a_{2}\lambda_{1}a_{1}^{T}=0 \]
则:
\[ \frac{\mathrm{d} F}{\mathrm{d} a_{2}}=2(\Sigma a_{2}^{T})^{T}-2\lambda a_{2}=0\\ \Rightarrow (\Sigma a_{2}^{T})^{T}-\lambda a_{2}=0\\ \Rightarrow (\Sigma a_{2}^{T})^{T}=\lambda a_{2}\\ \Rightarrow \Sigma a_{2}^{T}=\lambda a_{2}^{T} \]
同样根据矩阵的特征值与特征向量的概念,可以推出\(a_{2}^{T}\)是协方差矩阵的特征向量,\(\lambda\)是其对应的特征值。
我们的目的是最大化:\(a_{2}\Sigma a_{2}^{T}\),同样可根据以下变换:
\[ a_{2}\Sigma a_{2}^{T}=a_{2}(\Sigma a_{2}^{T})=a_{2}\lambda a_{2}^{T}=\lambda a_{2} a_{2}^{T}=\lambda \]
也就是说,我要取一个最大的\(\lambda\),但是我们在第一个主成分里已经取得了协方差矩阵\(\Sigma\)最大的特征值,那我们这里只能取第二大的特征值,此时求得的投影方向就是第二大特征值所对应的特征向量。
数学归纳
前面通过推导,我们可以求出第一个主成分和第二个主成分,具体我们求多少个主成分,看自己需求,每一个的求法和前面都差不多,唯一的区别在于优化问题中,要新增限制条件,新求的\(a_{i}\)必须保持与之前求得的\((a_{i-1},a_{i-2},....)\)全部保持正定。这样我们理论上就证明了如何通过协方差矩阵进行降维。
实际主成分分析(PCA降维算法)的算法流程
第一步:求协方差矩阵,
\[ \Sigma =\sum _{i=1}^{p}(X_{i}-\overline{X})(X_{i}-\overline{X})^{T} \]
第二步:求出上面的协方差矩阵的特征值,并按从大到小排列\((\lambda _{1},\lambda _{2},\lambda _{3},...)\)
对应的特征向量排序为\((a_{1}^{T},a_{2}^{T},a_{3}^{T},....)\)
第三步:归一化所有\(a_{i}\),使得\(a_{i}a_{i}^{T}=1\)
第四步:选取前m(m<n)个特征值所对应的特征向量,求出降维矩阵\(A\)
\[ A=\begin{bmatrix} a_{1}\\ a_{2}\\ ...\\ a_{m} \end{bmatrix}_{m\times n} \]
第五步:降维
\[ Y_{m\times 1}= \begin{bmatrix} a_{1}\\ a_{2}\\ ...\\ a_{m} \end{bmatrix}_{m\times n} \times (X_{n\times 1}-\overline{X_{n\times 1}}) = \begin{bmatrix} a_{1}(X_{n\times 1}-\overline{X_{n\times 1}})\\ a_{2}(X_{n\times 1}-\overline{X_{n\times 1}})\\ ...\\ a_{m}(X_{n\times 1}-\overline{X_{n\times 1}}) \end{bmatrix} \]
这样就把维度从\(n\times 1\)降成了\(m\times 1\)