主成分分析（Principal Component Analysis，PCA）

文章目录

1. 总体主成分分析
2. 样本主成分分析
3. 主成分分析方法

3.1 相关矩阵的特征值分解算法
3.2 矩阵奇异值分解算法

主成分分析（Principal Component Analysis，PCA）是一种常用的无监督学习方法
利用正交变换把由线性相关变量表示的观测数据 转换为 少数几个由线性无关变量表示的数据，线性无关的变量 称为 主成分
主成分的个数通常小于原始变量的个数，所以PCA属于降维方法
主要用于发现数据中的基本结构，即数据中变量之间的关系，是数据分析的有力工具，也用于其他机器学习方法的前处理
PCA属于多元统计分析的经典方法

1. 总体主成分分析

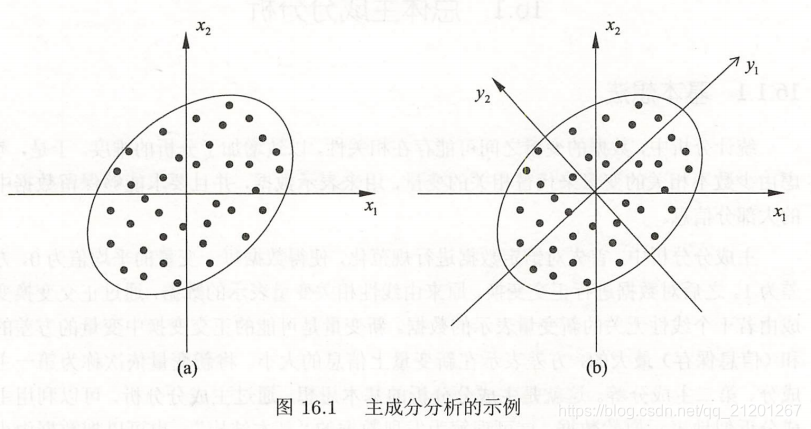
第一轴选取方差最大的轴 y1
在这里插入图片描述
主成分分析的主要目的是降维，所以一般选择 k（ $k\ll m$ ）个主成分（线性无关变量）来代替m个原有变量（线性相关变量），使问题得以简化，并能保留原有变量的大部分信息（原有变量的方差）。

在实际问题中，不同变量可能有不同的量纲，直接求主成分有时会产生不合理的结果。
为了消除这个影响，常常对各个随机变量实施规范化，使其均值为0，方差为1。

主成分分析的结果可以用于其他机器学习方法的输入。

将样本点投影到以主成分为坐标轴的空间中，然后应用聚类算法，就可以对样本点进行聚类

定义：

假设 $\pmb x$ 为 $m$ 维随机变量，均值为 $\mu$ ，协方差矩阵为 $\Sigma$
随机变量 $\pmb x$ 到 $m$ 维随机变量 $\pmb y$ 的线性变换
$y_i = \alpha_i^T \pmb x = \sum\limits_{k=1}^m \alpha_{ki}x_k, \quad i=1,2,...,m$
其中 $\alpha_i^T = (\alpha_{1i},\alpha_{2i},...,\alpha_{mi})$
如果该线性变换满足以下条件，称之为总体主成分：

$\alpha_i^T\alpha_i = 1, i = 1, 2,...,m$
$cov (y_i,y_j) = 0(i \neq j)$
$y_1$ 是 $\pmb x$ 的所有线性变换中方差最大的， $y_2$ 是与 $y_1$ 不相关的 $\pmb x$ 的所有线性变换中方差最大的，以此类推， $y_1,y_2,...,y_m$ 称为第一主成分…第 $m$ 主成分

假设 $\pmb x$ 是 $m$ 维随机变量，其协方差矩阵 $\Sigma$ 的特征值分别是 $\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_m \ge 0$ ，特征值对应的单位特征向量分别是 $\alpha_1,\alpha_2,...,\alpha_m$ ，则 $\pmb x$ 的第 $i$ 主成分可写作：
$y_i = \alpha_i^T \pmb x = \sum\limits_{k=1}^m \alpha_{ki}x_k, \quad i=1,2,...,m$
并且， $\pmb x$ 的第 $i$ 主成分的方差是协方差矩阵 $\Sigma$ 的第 $i$ 个特征值，即：
$var (y_i) = \alpha_i^T\Sigma\alpha_i = \lambda_i$

主成分性质：

主成分 $\pmb y$ 的协方差矩阵是对角矩阵 $cov(\pmb y) = \Lambda = diag(\lambda_1,\lambda_2,...,\lambda_m)$
主成分 $\pmb y$ 的方差之和等于随机变量 $\pmb x$ 的方差之和
$\sum\limits_{i=1}^m \lambda_i = \sum\limits_{i=1}^m \sigma_{ii}$
其中 $\sigma_{ii}$ 是 $x_i$ 的方差，即协方差矩阵 $\Sigma$ 的对角线元素
主成分 $y_k$ 与变量 $x_i$ 的相关系数 $\rho(y_k,x_i)$ 称为因子负荷量（factor loading），它表示第 $k$ 个主成分 $y_k$ 与变量 $x_i$ 的相关关系，即 $y_k$ 对 $x_i$ 的贡献程度
$\rho(y_k, x_i) = \frac{\sqrt{\lambda_k}\alpha_{ik}}{\sqrt{\sigma_{ii}}},k,i=1,2,...,m$

2. 样本主成分分析

是基于样本协方差矩阵的主成分分析
给定样本矩阵 $X$
在这里插入图片描述
$X$ 的样本协方差矩阵
$S = [s_{ij}]_{m \times n}, \quad s_{ij} = \frac{1}{n-1}\sum\limits_{k=1}^m(x_{ik}-\bar x_i)(x_{jk}-\bar x_j)\\ i = 1,2,...,m,\quad j = 1,2,...,m, 其中 \bar x_i = \frac{1}{n}\sum\limits_{k=1}^n x_{ik}$

给定样本 $X$ ，考虑 $\pmb x$ 到 $\pmb y$ 的线性变换 $\pmb y = A^T \pmb x$
在这里插入图片描述
如果满足以下条件，称之为样本主成分：

样本第一主成分 $y_1 = \alpha_1^T \pmb x$ 是在 $\alpha_1^T\alpha_1 = 1$ 条件下，使得 $\alpha_1^T \pmb x_j (j=1,2,...,n)$ 的样本方差 $\alpha_1^TS\alpha_1$ 最大的 $\pmb x$ 的线性变换，以此类推。
样本第 $i$ 主成分 $y_i = \alpha_i^T \pmb x$ 是在 $\alpha_i^T\alpha_i = 1$ 和 $\alpha_i^T\pmb x_j$ 与 $\alpha_k^T \pmb x_j \quad(k < i,j = 1,2,...,n)$ 的样本协方差 $\alpha_k^TS\alpha_i=0$ 条件下，使得 $\alpha_i^T \pmb x_j (j=1,2,...,n)$ 的样本方差 $\alpha_i^TS\alpha_i$ 最大的 $\pmb x$ 的线性变换