PCA原理:
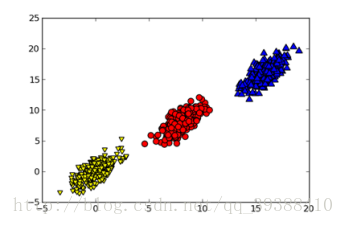
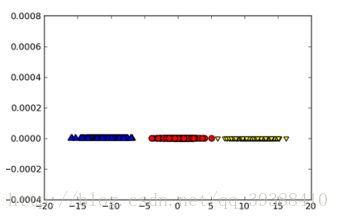
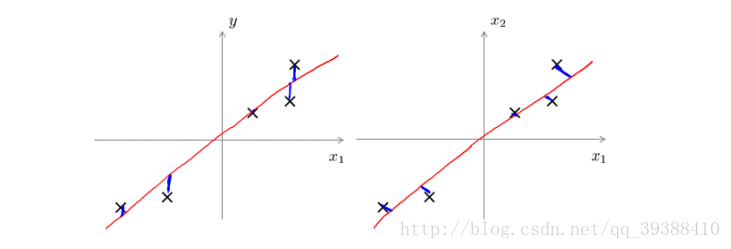
通常情况下,在收集数据集时会有很多的特征,这代表着数据是高冗余的表示,但是对于某个工程来说其实可能并不需要那么多的特征。所以就需要给数据进行降维(Dimensionality Reduction)。降维可以简化数据,使数据集更易使用,降低时间开销,而且能减少一部分噪音的影响,使最后的效果变好。比如上图中,如果进行降维后再进行分类,将会易于处理。
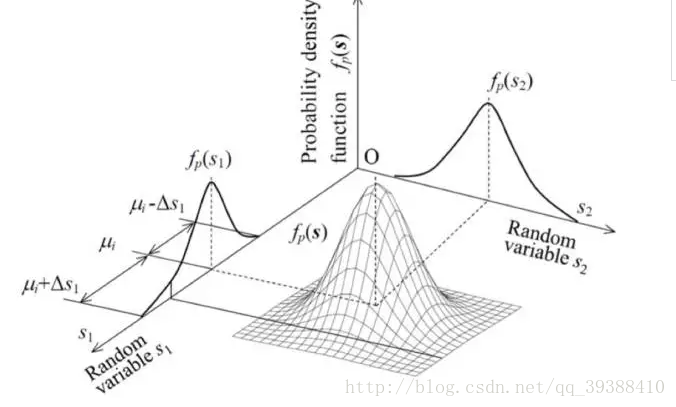
主成分分析(Principal Component Analysis,PCA),顾名思义就是找出最主要的成分来代替就好,那么如何选择最主要的成分来代替能使误差最小呢?即如何选择能最大的代替原来的数据。
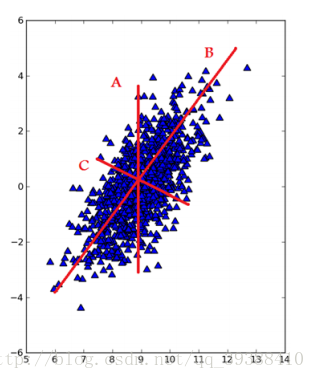
PCA的目的就是找到一个方向向量,当我们投影在这个方向上时,希望它的方差尽可能大,均方误差尽可能的小,这样做可以保证所有的点都尽可能的离这条线近。比如在上图,不用想也能明白哪一个方向是最好的。不过这里的均方误差,有必要和线性回归的代价函数做一下比较,一个是投影误差,一个是预测误差。
为了将数据从原来的坐标系转移到了新的坐标系,新的坐标系将由数据本身决定,第一个新坐标是方差最大的方向,其他的是与第一个方向方向正交且具有最大方差的方向。因为发现大部分方差都包含在前几个新坐标中,因此可以忽略余下的坐标轴,从而保证了数据的特征的最小损失。那么可以求出其协方差矩阵来判断。证明一下,如果对于任意一个点
算法实现:(Python)
def pca(dataMat, topNfeat=9999999):#topNfeat是应用的前N个特征,不指定就返回前999999
meanVals = mean(dataMat, axis=0)
meanRemoved = dataMat - meanVals #去平均值
covMat = cov(meanRemoved, rowvar=0)#协方差
eigVals,eigVects = linalg.eig(mat(covMat))#特征值
eigValInd = argsort(eigVals)#从小到大排序
eigValInd = eigValInd[:-(topNfeat+1):-1]
redEigVects = eigVects[:,eigValInd]#topN的特征向量
lowDDataMat = meanRemoved * redEigVects#转换新空间
reconMat = (lowDDataMat * redEigVects.T) + meanVals
return lowDDataMat, reconMatPCA应用:
PCA参数说明:
PCA(copy=True, iterated_power=’auto’, n_components=None, random_state=None,svd_solver=’auto’, tol=0.0, whiten=False)
copy=True:是否复制
iterated_power='auto':迭代
n_components=None:降维特征数目
random_state=None:随机状态
svd_solver='auto':自否采用SVD
tol=0.0:容忍度
whiten=False:是否特征归一化
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA#导入PCA模块
from mpl_toolkits.mplot3d import Axes3D#绘制3D散点图
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
iris=datasets.load_iris()
x=iris.data[:,1]
y=iris.data[:,2]
species=iris.target
x_reduced=PCA(n_components=3).fit_transform(iris.data)
fig=plt.figure()
ax=Axes3D(fig)
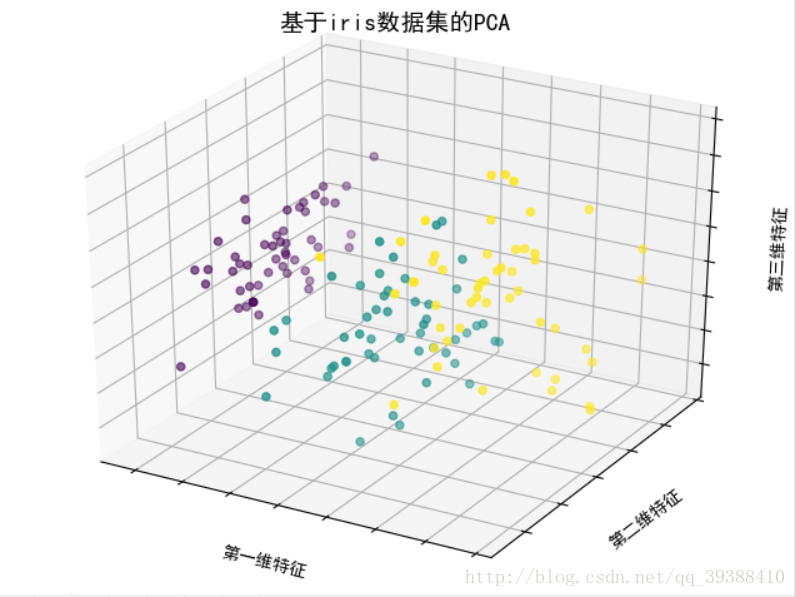
ax.set_title('基于iris数据集的PCA',size=14)#设置题目
ax.scatter(x_reduced[:,0],x_reduced[:,1],x_reduced[:,2],c=species)
ax.set_xlabel('第一维特征')#设置x轴标签
ax.set_ylabel('第二维特征')
ax.set_zlabel('第三维特征')
ax.w_xaxis.set_ticklabels(())#去除刻度文本,便于观察数据
ax.w_yaxis.set_ticklabels(())
ax.w_zaxis.set_ticklabels(())
plt.show()
现在让我们换个角度理解PCA,PCA的目的不就是找个新的基坐标来减少维度(自由度)吗?然后再根据基坐标重建整个数据。那么目标函数就可以变为了要最小化这个重建的误差,然后同样的也可以推导出类似上面方法的目标形式。那么关键是这个视角与第一种的差距在哪呢?可以看出一个是为了找主成分,一个直接进行维度缩减。所以其实从某种角度上来看,这个视角或许才是更适合PCA降维的理解。
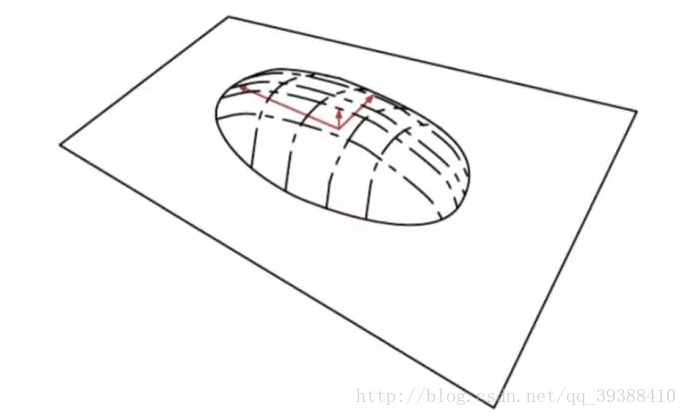
《Deep Learning》一书中打过的比方–烙饼空间(Pancake), 而在烙饼空间里面找一个线性流行就是PCA的另一种理解,即把数据概率值看成是空间!!。