前言
典例剖析
(1).求椭圆\(C\)的标准方程;
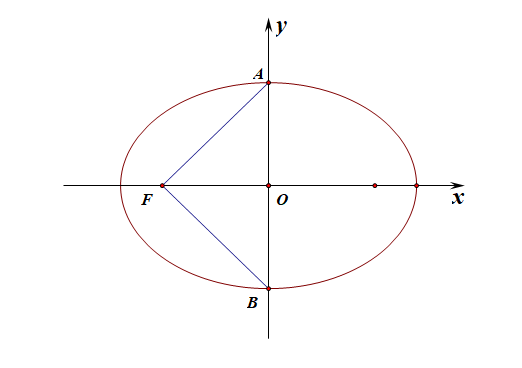
分析:示意图如图所示,由于\(S_{\triangle ABF}=1\),即\(\cfrac{1}{2}\cdot c\cdot 2b=1\),则\(bc=1\);
又由于\(e=\cfrac{c}{a}=\cfrac{\sqrt{2}}{2}\),则\(a=2k(k>0)\),\(c=\sqrt{2}k\),则\(b^2=a^2-c^2=2k^2\),\(b=\sqrt{2}k\),
由\(bc=1=2k^2\),解得\(k=\cfrac{\sqrt{2}}{2}\),故\(a=\sqrt{2}\),\(b=1\),
所以椭圆\(C\)的标准方程为\(\cfrac{x^2}{2}+y^2=1\);
(2).过点\(D(2,0)\)的直线\(l\)与椭圆\(C\)交于不同的两点\(M\),\(N\)(\(M\)在\(D\),\(N\)之间),求\(\frac{S_{\triangle ODM}}{S_{\triangle ODN}}\)(\(O\)为坐标原点)的取值范围;
分析:设\(M(x_1,y_1)\),\(N(x_2,y_2)\),
由于直线恒过点\(D(2,0)\),故可设直线\(l\)的方程为\(x=my+2\),
与椭圆方程\(\cfrac{x^2}{2}+y^2=1\)联立,

消掉\(x\)得到,\((m^2+2)y^2+4my+2=0\),
由\(\Delta=8m^2-16>0\),解得\(m^2>2\),
又由韦达定理得到,\(y_1+y_2=-\cfrac{4m}{m^2+2}\),\(y_1y_2=\cfrac{2}{m^2+2}\);
令\(\frac{S_{\triangle ODM}}{S_{\triangle ODN}}=\cfrac{|y_1|}{|y_2|}=t\)(则由于\(|y_1|<|y_2|\),则\(0<t<1\);且\(y_1\),\(y_2\)同号)
又由于\(\cfrac{(y_1+y_2)^2}{y_1y_2}=\cfrac{y_1^2+y_2^2+2y_1y_2}{y_1y_2}=\cfrac{y_1}{y_2}+\cfrac{y_2}{y_1}+2=t+\cfrac{1}{t}+2\);
且\(\cfrac{(y_1+y_2)^2}{y_1y_2}=\cfrac{8m^2}{m^2+2}=\cfrac{8}{1+\frac{2}{m^2}}\);
由于\(m^2>2\),则得到\(4<\cfrac{8}{1+\frac{2}{m^2}}<8\),故得到\(4<t+\cfrac{1}{t}+2<8\),
结合\(0<t<1\),解得\(3-2\sqrt{2}<t<1\),
所以\(\frac{S_{\triangle ODM}}{S_{\triangle ODN}}\)的取值范围为\((3-2\sqrt{2},1)\);
名师点评:本题考查椭圆的标准方程、直线与椭圆的位置关系;考查函数与方程、转化与划归思想;考查数学运算、逻辑推理等核心素养。
分析:求\(\Delta APF\)面积的最小值,其中边AF长度固定,故只需要求边AF上的高线的最小值即可。
法1、平行线法,如图1所示,容易知道点\(F(3,0)\),故直线\(AF:2\sqrt{6}x+y-6\sqrt{6}=0\),
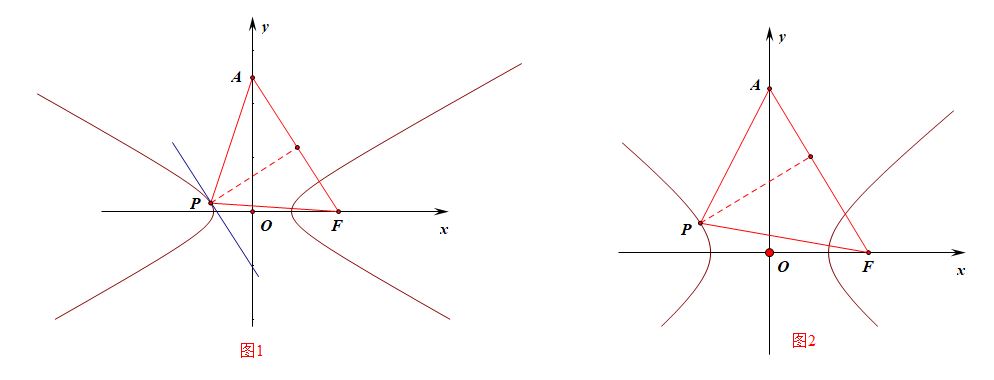
设\(l\)和直线AF平行且和双曲线的左支相切与点P,故直线\(l:2\sqrt{6}x+y+m=0\),
联立\(2\sqrt{6}x+y+m=0\)和\(x^2-\cfrac{y^2}{8}=1\),消\(y\)得到\(16x^2+4\sqrt{6}mx+m^2+8=0\),
由于相切得到\(\Delta =96m^2-4\times16(m^2+8)=0\),解得\(m=\pm 4\),结合图像将\(m=-4舍弃\),
即直线\(l:2\sqrt{6}x+y+4=0\),故三角形的高的最小值即两条平行线的间距,
故AF边上的高\(h=\cfrac{|4-(-6\sqrt{6})|}{\sqrt{(2\sqrt{6})^2+1}}=\cfrac{6\sqrt{6}+4}{5}\),
故\(S_{min}=\cfrac{1}{2}\times|AF|\times \cfrac{6\sqrt{6}+4}{5}=\cfrac{1}{2}\times15\times \cfrac{6\sqrt{6}+4}{5}=9\sqrt{6}+6\)。
法2、函数法,如图2所示,由题目可知双曲线的左支对应的函数为\(y=f(x)=\pm\sqrt{8x^2-8}(x<0)\),
设点\(P(x_0,y_0)\),则\(f'(x)=\pm\cfrac{1}{2\sqrt{8x^2-8}}\cdot 16x=\pm\cfrac{8x}{\sqrt{8x^2-8}}\),
结合图像可知\(f'(x)<0\),故取\(f'(x)=\cfrac{8x}{\sqrt{8x^2-8}}(x<0)\),当\(f'(x)=k_{AF}=-2\sqrt{6}\)时,
AF边上的高线最小(可结合平行线法理解),故\(\cfrac{8x_0}{\sqrt{8x_0^2-8}}=-2\sqrt{6}\),
解得\(x_0=-\cfrac{\sqrt{6}}{2}\),代入得到\(y=2\),即切点\(P(-\cfrac{\sqrt{6}}{2},2)\),
故高\(h=\cfrac{|2\sqrt{6}\cdot(-\cfrac{\sqrt{6}}{2})+2-6\sqrt{6}|}{5}=\cfrac{6\sqrt{6}+4}{5}\),
故\(S_{min}=\cfrac{1}{2}\times|AF|\times \cfrac{6\sqrt{6}+4}{5}=\cfrac{1}{2}\times15\times \cfrac{6\sqrt{6}+4}{5}=9\sqrt{6}+6\)。
法3、参数方程法,不要求学生掌握。由于双曲线为\(x^2-\cfrac{y^2}{8}=1\),
故其参数方程为\(\begin{cases}x=\cfrac{1}{cos\theta}\\y=2\sqrt{2}tan\theta\end{cases}(\theta为参数)\),
故\(h=\cfrac{|\cfrac{2\sqrt{6}}{cos\theta}+2\sqrt{2}tan\theta-6\sqrt{6}|}{5}=\cfrac{|\cfrac{2\sqrt{6}}{cos\theta}+\cfrac{2\sqrt{2}sin\theta}{cos\theta}-6\sqrt{6}|}{5}\),
以下难点转化为求\(\cfrac{2\sqrt{6}}{cos\theta}+\cfrac{2\sqrt{2}sin\theta}{cos\theta}\)的值。
令\(m=\cfrac{2\sqrt{6}}{cos\theta}+\cfrac{2\sqrt{2}sin\theta}{cos\theta}\),
则有\(2\sqrt{6}+2\sqrt{2}sin\theta=mcos\theta\),故\(\sqrt{m^2+8}cos\theta=2\sqrt{6}\),
即\(cos\theta=\cfrac{2\sqrt{6}}{\sqrt{m^2+8}}\),故\(|cos\theta|=|\cfrac{2\sqrt{6}}{\sqrt{m^2+8}}|\leq 1\),
解得\(m\ge 4\)或者\(m\leq -4\),由于参数\(\theta\in(0,\pi)\),且点P在左支,
故\(\theta\in(\cfrac{\pi}{2},\pi)\),故\(m<0\),故当\(m=-4\)时\(d\)有最小值,
此时\(d_{min}=\cfrac{|-4-6\sqrt{6}|}{5}=\cfrac{4+6\sqrt{6}}{5}\),
故\(S_{min}=\cfrac{1}{2}\times|AF|\times \cfrac{6\sqrt{6}+4}{5}=\cfrac{1}{2}\times15\times \cfrac{6\sqrt{6}+4}{5}=9\sqrt{6}+6\)。
分析:如下图所示,可知圆\(F_2\)的圆心为\(F_2(c,0)\),半径为\(r=\cfrac{c}{2}\),由于圆和双曲线都关于坐标轴对称,故只需要保证圆和一条渐近线\(y=\cfrac{b}{a}x\)有公共点即可,
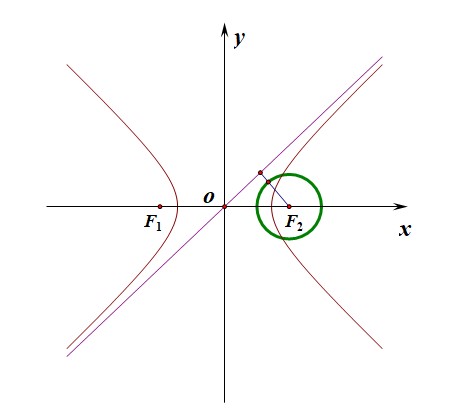
此时可以使用联立直线方程和双曲线的方程,使用\(\Delta \ge 0\)的思路,也可以利用圆心到直线的距离小于半径的思路,很明显第二个思路的运算量要小一些。
此时圆心为\(F_2(c,0)\),半径为\(r=\cfrac{c}{2}\),直线为\(bx-ay=0\),故\(d=\cfrac{|bc-a\times 0|}{\sqrt{a^2+b^2}}\leq \cfrac{c}{2}\),
化简整理得到,\(2b\leq c\),即\(4b^2\leq c^2\),则\(4c^2-4a^2\leq c^2\),整理为\(\cfrac{c^2}{a^2}\leq \cfrac{4}{3}\),故\(e\leq \cfrac{2\sqrt{3}}{3}\),又双曲线的\(e>1\),故\(e\in (1,\cfrac{2\sqrt{3}}{3}]\).
分析:设\(A(x_1,y_1)\),\(B(x_2,y_2)\),弦\(AB\)的垂直平分线交\(x\)轴于点\(C(t,0)\),
\(AB\)的中点为\(M(x_0,y_0)\),则\(x_0>\sqrt{6}\),

由题意有\(\cfrac{x_1^2}{6}-\cfrac{y_1^2}{3}=1\)①,\(\cfrac{x_2^2}{6}-\cfrac{y_2^2}{3}=1\)②,两式相减得到,
\((x_1+x_2)(x_1-x_2)-2(y_1+y_2)(y_1-y_2)=0\),于是有\(x_0(x_1-x_2)-2y_0(y_1-y_2)=0\),
即\(k_{AB}=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{x_0}{2y_0}\),又\(k_{MC}=\cfrac{y_0}{x_0-t}\),由\(k_{AB}\cdot k_{MC}=-1\)得到,
\(\cfrac{y_0}{x_0-t}\cdot \cfrac{x_0}{2y_0}=-1\),即\(x_0+2(x_0-t)=0\),则\(t=\cfrac{3x_0}{2}>\cfrac{3\sqrt{6}}{2}\)。
故\(t\in (\cfrac{3\sqrt{6}}{2},+\infty)\)。
法1:做出如下的示意图,设直线\(AB\)的斜率为\(k\),不妨只考虑\(k>0\),则\(AB:y=k(x-4)\),即\(kx-y-4k=0\);
将直线和抛物线方程联立,消去\(x\)得到,\(ky^2-4y-16k=0\),则\(y_1+y_2=-\cfrac{-4}{k}=\cfrac{4}{k}\),\(y_1y_2=-16\),
则\(|AB|=\sqrt{1+\cfrac{1}{k^2}}|y_1-y_2|=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(y_1+y_2)^2-4y_1y_2}\)
\(=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(\cfrac{4}{k})^2-4\times (-16)}=\sqrt{\cfrac{k^2+1}{k^2}}\cdot 4\cdot \sqrt{\cfrac{4k^2+1}{k^2}}\)
\(=4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\),
又点\(F\)到直线\(AB\)的距离为\(d=h=\cfrac{|3k|}{\sqrt{k^2+1}}=\cfrac{3k}{\sqrt{k^2+1}}\),
则\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\cdot \cfrac{3k}{\sqrt{k^2+1}}\)
\(=6\times \cfrac{\sqrt{4k^2+1}}{k}=6\times \sqrt{4+\cfrac{1}{k^2}}\),
当\(k\rightarrow \infty\)时,所求面积有最小值,\(S_{min}=6\times 2=12\)。故选\(B\).
法2:仿上利用均值不等式可以说明,当\(AB\)和\(x\)轴垂直时,\(S_{\triangle ABF}\)有最小值;
\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 3\cdot (|y_1|+|y_2|)\ge \cfrac{3}{2}\cdot 2\sqrt{|y_1y_2|}= \cfrac{3}{2}\cdot 2\cdot 4=12\),故选\(B\).
解析:由\(\overrightarrow{AP}=(\lambda-1)\overrightarrow{OA}\),即\(\overrightarrow{OP}-\overrightarrow{OA}=(\lambda-1)\overrightarrow{OA}\)
则有\(\overrightarrow{OP}=\lambda\overrightarrow{OA}\),故\(O、P、A\)三点共线,即夹角\(\theta=0\)
由\(\overrightarrow{OA}\cdot \overrightarrow{OP}=12\),得到\(|\overrightarrow{OA}|\cdot |\overrightarrow{OP}|=12\),

设OP与\(x\)轴的夹角为\(\theta\),点\(A(x,y)\),\(B\)为点\(A\)在\(x\)轴上的投影,由图可知,线段\(OP\)在\(x\)轴上的投影长度为\(||\overrightarrow{OP}|\cdot cos\theta|\)
则\(||\overrightarrow{OP}|\cdot cos\theta|=|\overrightarrow{OP}|\times \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|}\)
\(=\cfrac{12}{|\overrightarrow{OA}|}\times \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|}\)
\(=12\cdot \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|^2}\),\(|\overrightarrow{OB}|=|x|\),\(|\overrightarrow{OA}|=\sqrt{x^2+y^2}\),
\(=12\times \cfrac{|x|}{x^2+y^2}\), 接下来施行变量集中,由于\(\cfrac{x^2}{16}+\cfrac{y^2}{8}=1\),得到\(y^2=8-\cfrac{x^2}{2}\),代入
\(=12\times \cfrac{|x|}{\cfrac{x^2}{2}+8}\),分子分母同除以\(|x|\)得到,
\(=12\times \cfrac{1}{\frac{|x|}{2}+\frac{8}{|x|}}\leq 12\times \cfrac{1}{4}=3\),
当且仅当\(|x|=4\)时等号成立,故线段\(OP\)在\(x\)轴上的投影长度的最大值为\(3\)。