圆锥曲线的定值定点问题

前言

典例剖析

例1 【衡水金卷，直线过定点类型】如图所示，已知点\(A(-1，0)\)是抛物线的准线与\(x\)轴的交点，过点\(A\)的直线与抛物线交于点\(M，N\)两点，过点\(M\)的直线交抛物线于另一个点\(Q\)，且直线\(MQ\)过点\(B(1，-1)\).

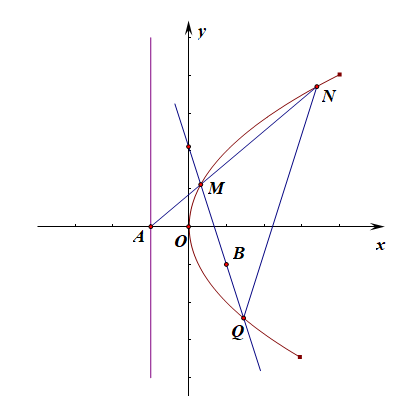
(1).求抛物线的方程。

分析：由题目图形可知，\(\cfrac{p}{2}=1\)，则\(p=2\)，

故顶点在坐标原点，开口向右的抛物线的方程为\(y^2=2px\)，即\(y^2=4x\)。

(2).求证：直线\(QN\)过定点。

分析：如果直线过定点\((m，n)\)，则直线的表达式必然应该能化为：\(y-n=k(x-m)\)类型。

设点\(M(4t^2，4t)\)，点\(N(4t_1^2，4t_1)\)，点\(M(4t_2^2，4t_2)\)，

则由题目易知直线\(MN\)的斜率存在，且\(k_{MN}=\cfrac{4t-4t_1}{4t^2-4t_1^2}=\cfrac{1}{t+t_1}\)，

从而直线\(MN\)的方程是\(y=\cfrac{1}{t+t_1}(x-4t^2)+4t\)，即\(x-(t+t_1)y+4tt_1=0\)。

同理可知，直线\(MQ\)的方程\(x-(t+t_2)y+4tt_2=0\)，直线\(NQ\)的方程\(x-(t_1+t_2)y+4t_1t_2=0\)，

又点\(A\)在直线\(MN\)上，从而有\(4tt_1=1\)，即\(t=\cfrac{1}{4t_1}\)；

点\(B\)在直线\(MQ\)上，从而有\(1+(t+t_2)+4tt_2=0\)，

即\(1+(\cfrac{1}{4t_1}+t_2)+4\times \cfrac{1}{4t_1}t_2=0\)，

化简得到\(4t_1t_2=-4(t_1+t_2)-1\)，

代入\(NQ\)的方程，得到\(x-(t_1+t_2)y-4(t_1+t_2)-1=0\)，

即\(y+4=\cfrac{1}{t_1+t_2}(x-1)\)，故直线\(NQ\)经过定点\((1，-4)\)。

• 抛物线\(y^2=4x\)上的任意点的坐标的设法一般是\((x，y)\)，本题采用\((4t^2，4t)\)，是抛物线的参数方程的一种。

• 注意直线过定点的证明思路；

• 延伸阅读：直线或函数恒过定点；