逻辑斯蒂回归和感知机的异同:
两类都是线性分类器;
损失函数两者不同:逻辑斯蒂回归使用极大似然(对数损失函数),感知机使用的是均方损失函数(即错误点到分离平面的距离,最小化这个值)
逻辑斯蒂比感知机的优点在于对于激活函数的改进。
前者为sigmoid function,后者为阶跃函数。这就导致LR是连续可导,而阶跃函数则没有这个性质。
LR使得最终结果有了概率解释的能力(将结果限制在0-1之间),sigmoid为平滑函数,能够得到更好的分类结果,而step function为分段函数,对于分类的结果处理比较粗糙,非0即1,而不是返回一个分类的概率。
逻辑斯蒂回归为什么不能用均方损失作为损失函数
首先设想一下,目标函数为 ,并不是不可以求解,那为什么不用呢?
知乎大神解决了我的疑惑:
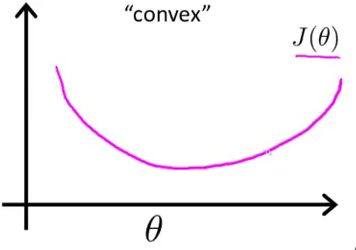
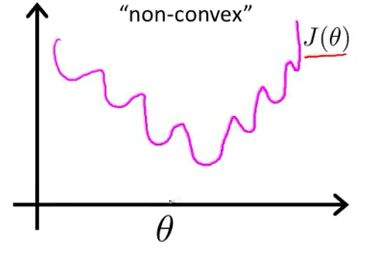
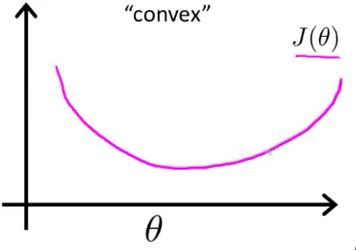
如果用最小二乘法,目标函数就是 ,是非凸的,不容易求解,会得到局部最优。
最小二乘作为损失函数的函数曲线:
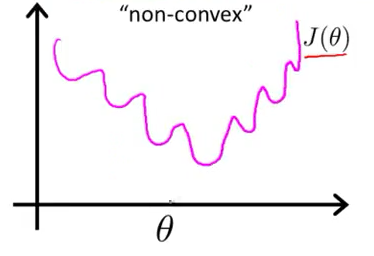
最小二乘作为逻辑回归模型的损失函数,theta为待优化参数
如果用最大似然估计,目标函数就是对数似然函数: ,是关于
的高阶连续可导凸函数,可以方便通过一些凸优化算法求解,比如梯度下降法、牛顿法等。
最大似然作为损失函数的函数曲线(最大似然损失函数后面给出):