逻辑斯蒂回归和感知机的异同:
两类都是线性分类器;
损失函数两者不同:逻辑斯蒂回归使用极大似然(对数损失函数),感知机使用的是均方损失函数(即错误点到分离平面的距离,最小化这个值)
逻辑斯蒂比感知机的优点在于对于激活函数的改进。
前者为sigmoid function,后者为阶跃函数。这就导致LR是连续可导,而阶跃函数则没有这个性质。
LR使得最终结果有了概率解释的能力(将结果限制在0-1之间),sigmoid为平滑函数,能够得到更好的分类结果,而step function为分段函数,对于分类的结果处理比较粗糙,非0即1,而不是返回一个分类的概率。
逻辑斯蒂回归为什么不能用均方损失作为损失函数呢:
首先设想一下,目标函数为 ,并不是不可以求解,那为什么不用呢?
知乎大神解决了我的疑惑:
如果用最小二乘法,目标函数就是 ,是非凸的,不容易求解,会得到局部最优。
最小二乘作为损失函数的函数曲线:
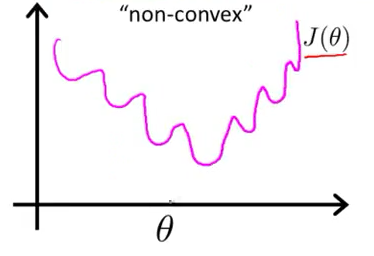
最小二乘作为逻辑回归模型的损失函数,theta为待优化参数
如果用最大似然估计,目标函数就是对数似然函数: ,是关于
的高阶连续可导凸函数,可以方便通过一些凸优化算法求解,比如梯度下降法、牛顿法等。
最大似然作为损失函数的函数曲线(最大似然损失函数后面给出):
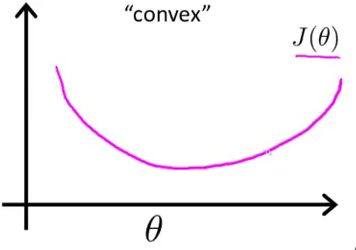
再来附加一个大神的推导:
面来推一下逻辑回归中最大损失函数到底是怎么来的,因为我看到很多地方只是说了一下用到最大似然的方法,就直接给出了最终的形式,还看到有书里面过程搞错了,也给出了最终的正确形式。
既然是最大似然,我们的目标当然是要最大化似然概率了:
对于二分类问题有:
用一个式子表示上面这个分段的函数为:(记得写成相乘的形式)
代入目标函数中,再对目标函数取对数,则目标函数变为:
如果用 来表示
,则可用
来表示
,再将目标函数max换成min,则目标函数变为:
这样就得到最终的形式了!
作者:临熙
链接:https://www.zhihu.com/question/65350200/answer/266277291
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
逻辑斯蒂回归中的极大似然是什么?极大似然,对数损失函数,交叉熵之间的区别联系:
逻辑斯蒂回归使用的是极大似然就相当于最小化负的似然函数,从损失函数的角度来看就变成了对数损失
极大似然和交叉熵之间的表现形式一样。好神奇,有空继续补充