离散周期信号傅里叶级数 — Fourier Series of Discrete-Time Periodic Signals

连续信号通常是数学领域里的理论研究对象，而现实生活中我们遇到的信号往往是离散的，且计算机只能处理有限长度的离散信号。所以为了让傅立叶分析解决实际问题，有必要将其推广到离散信号领域。【阅读本文前，建议先了解连续周期信号傅里叶级数】

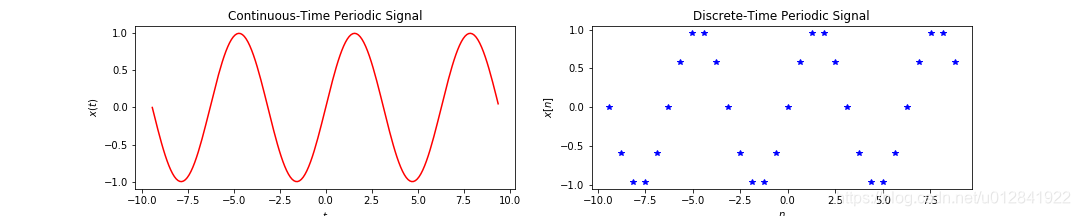
连续周期信号和离散周期信号如上图：左图为连续周期正弦波 $x(t)=x(t+T)$，其中周期 $T=2\pi$；右图为左图正弦波的周期离散采样， $x[n]=x[n+N]$，其中周期 $N=10$。

和连续周期信号傅立叶级数基于一样的猜想，离散周期信号傅立叶级数是想寻得一组不同振幅、不同频率和不同相位的正弦离散函数以表达某离散周期信号。即：
$x[n] = C + \sum_{k=1}^{\infty}a_{k}\sin(kw_{0}n) + \sum_{k=1}^{\infty}b_{k}\cos(kw_{0}n)$
其中 $w_{0}=\frac{2\pi}{N}$。根据欧拉公式 $e^{ix}=\cos(x)+i\sin(x)$得：
$\begin{cases} \cos(x) = \frac{e^{ix}+e^{-ix}}{2} \\ \sin(x) = \frac{e^{ix}-e^{-ix}}{2i} \end{cases}$

因此，上式可推导为：
$\begin{aligned} & x[n] = C + \sum_{k=1}^{\infty}(a_{k}\frac{e^{ikw_{0}n}-e^{-ikw_{0}n}}{2i} + b_{k}\frac{e^{ikw_{0}n}+e^{-ikw_{0}n}}{2}) \\ & = C + \sum_{k=1}^{\infty}(\frac{ia_{k}-b_{k}}{2}e^{ikw_{0}n} + \frac{-ia_{k}-b_{k}}{2}e^{-ikw_{0}n}) \\ \end{aligned}$
令 $A_{k} = \frac{ia_{k}-b_{k}}{2}$和 $B_{k} = \frac{-ia_{k}-b_{k}}{2}$，得到 $x[n]的傅立叶级数复数形式的表达式$：
$\begin{aligned} & x[n] = Ce^{i0w_{0}n} + \sum_{k=1}^{\infty}A_{k}e^{ikw_{0}n} + \sum_{k=1}^{\infty}B_{k}e^{-ikw_{0}n} \\ & = \sum_{k=-1}^{-\infty}B_{-k}e^{ikw_{0}n} + Ce^{i0w_{0}n} + \sum_{k=1}^{\infty}A_{k}e^{ikw_{0}n} \\ & = \sum_{k=-\infty}^{\infty}D_{k}e^{ikw_{0}n} \end{aligned}$

我们接着观察该级数中的单项 $e^{ikw_{0}n}$：
$\phi_{k}[n] = e^{ikw_{0}n} = e^{ik\frac{2\pi}{N}n}, n=0,\pm1,\pm2, \dots$
先说结论： $\phi_{k}[n]=\phi_{k+rN}[n]$，其中 $k=0,\pm1,\pm2, \dots$、 $r=0,1,2,\dots$、 $N$为离散信号 $x[n]$的变化周期。证明过程如下：
$\begin{aligned} & \phi_{k+rN}[n] = e^{i(k+rN)\frac{2\pi}{N}n}=e^{ik\frac{2\pi}{N}n}e^{ir{2\pi}n} = e^{ik\frac{2\pi}{N}n}(e^{i{2\pi}})^{rn} \\ & = e^{ik\frac{2\pi}{N}n}(\cos(2\pi) +i\sin(2\pi))^{rn} \\ & = e^{ik\frac{2\pi}{N}n}(1)^{rn} \\ & = e^{ik\frac{2\pi}{N}n} = \phi_{k}[n] \end{aligned}$

因此，得到离散周期信号 $x[n]$的傅立叶级数如下：
$x[n] = \sum_{k=<N>}^{}X_{k}e^{ik\frac{2\pi}{N}n}$

给出： $\sum_{n=<N>}^{}e^{ik\frac{2\pi}{N}n} = \begin{cases} N, & k=0, \pm{N}, \pm{2N}, \dots \\ 0, & otherwise \end{cases}$ 令 $S = \sum_{n=<N>}^{}e^{ik\frac{2\pi}{N}n}$，证明过程如下： $S(1^{\frac{k}{N}}-1) = e^{ik\frac{2\pi}{N}}S-S = e^{ik\frac{2\pi}{N}N} - e^{ik\frac{2\pi}{N}0} = e^{ik{2\pi}} - 1=1^{k}-1 = 0$ 由上式可知，当 $k \neq 0, \pm{N}, \pm{2N}, \dots$时： $(1^{\frac{k}{N}}-1) \neq 0 且 S = \sum_{n=<N>}^{}e^{ik\frac{2\pi}{N}n} = 0$ 当 $k = 0, \pm{N}, \pm{2N}, \dots$时： $S = \sum_{n=<N>}^{}e^{ik\frac{2\pi}{N}n} = \sum_{n=<N>}^{}(e^{i2\pi} )^{\frac{k}{N}n} = \sum_{n=<N>}^{}(1)^{rn} = N, r = 0,\pm1,\pm2,\dots$

现在，对离散周期信号 $x[n]$每时刻的信号求和，并乘以 $e^{-ir\frac{2\pi}{N}n}$得：
$\sum_{n=<N>}^{} x[n] e^{-ir\frac{2\pi}{N}n} = \sum_{n=<N>}^{} \sum_{k=<N>}^{}X_{k}e^{i(k-r)\frac{2\pi}{N}n} = \sum_{k=<N>}^{} X_{k} \sum_{n=<N>}^{}e^{i(k-r)\frac{2\pi}{N}n}$
由上面给出的公式可以得出，当 $k-r=0$时， $\sum_{n=<N>}^{}e^{i(k-r)\frac{2\pi}{N}n} = N$；当 $k-r \neq 0$时， $\sum_{n=<N>}^{}e^{i(k-r)\frac{2\pi}{N}n} = 0$。所以：
$\sum_{n=<N>}^{} x[n] e^{-ir\frac{2\pi}{N}n} = \sum_{k=<N>}^{} X_{k} \sum_{n=<N>}^{}e^{i(k-r)\frac{2\pi}{N}n} = X_{r} N$
即：
$X_{r} = \frac{1}{N} \sum_{n=<N>}^{} x[n] e^{-ir\frac{2\pi}{N}n}$

至此，我们已经得到离散周期信号 $x[n]$的傅立叶级数（如下）：
$x[n] = \sum_{k=<N>}^{}X_{k}e^{ik\frac{2\pi}{N}n}$
其中， $X_{k} = \frac{1}{N} \sum_{n=<N>}^{} x[n] e^{-ik\frac{2\pi}{N}n}$。