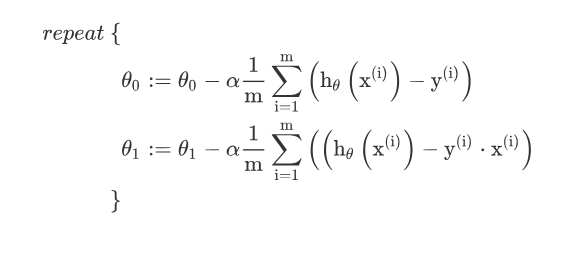版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/flyfish1986/article/details/86909160
作者:邵盛松
本文中描述的高中教科书是 人民教育出版社B版,高中教科书 《数学 选修 1-2》的第一章《“回归”一词的由来》22页
英国的统计学家弗朗西斯·高尔顿(Francis Galton,1822—1911)用统计方法研究两个变量之间关系。他研究父母身高与子女身高之间的关系,“回归”这个词由他引入的。
假设你是一个老板,想到其他城市再开一家分店,你拥有一份城市人口数对应收益的数据,问当一个城市有8 百万人,那么这家分店收益是多少?
人口(百万)
收益(亿元)
1
6
2
5
3
7
4
10
回归公式
高中教科书《数学2 必修》中的《直线的方程》74页点斜式方程
k
=
y
2
−
y
1
x
2
−
x
1
k = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } }
k = x 2 − x 1 y 2 − y 1
y
2
−
y
1
=
k
(
x
2
−
x
1
)
y_2 - y _ { 1 } = k \left( x_2 - x _ { 1 } \right)
y 2 − y 1 = k ( x 2 − x 1 ) 斜截式方程
y
=
k
x
+
b
y = k x + b
y = k x + b 两点式方程
y
−
y
1
y
2
−
y
1
=
x
−
x
1
x
2
−
x
1
(
x
1
≠
x
2
,
y
1
≠
y
2
)
\frac { y - y _ { 1 } } { y _ { 2 } - y _ { 1 } } = \frac { x - x _ { 1 } } { x _ { 2 } - x _ { 1 } } (x _ { 1 } \neq { x _ { 2 } },y _ { 1 } \neq { y _ { 2 } })
y 2 − y 1 y − y 1 = x 2 − x 1 x − x 1 ( x 1 ̸ = x 2 , y 1 ̸ = y 2 ) 一般式
x
,
y
x,y
x , y
A
x
+
B
y
+
C
=
0
(
(
A
2
+
B
2
≠
0
)
)
\mathrm { Ax } + \mathrm { By } + \mathrm { C } = 0 (\left( A ^ { 2 } + B ^ { 2 } \neq 0 \right))
A x + B y + C = 0 ( ( A 2 + B 2 ̸ = 0 ) )
斜率 (图片来自wiki)
k
=
tan
θ
=
y
2
−
y
1
x
2
−
x
1
=
Δ
y
Δ
x
k = \tan \theta = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } = \frac { \Delta y } { \Delta x }
k = tan θ = x 2 − x 1 y 2 − y 1 = Δ x Δ y
导数
在3Blue1Brown的《微积分的本质 - 02 - 导数的悖论》详细介绍了导数的意义
d
t
dt
d t
d
t
dt
d t
d
s
ds
d s
v
(
t
)
v(t)
v ( t )
d
s
d
t
=
s
(
t
+
d
t
)
−
s
(
t
)
d
t
\frac{ds}{dt}=\frac{s(t+dt)-s(t)}{dt}
d t d s = d t s ( t + d t ) − s ( t )
=
lim
h
→
0
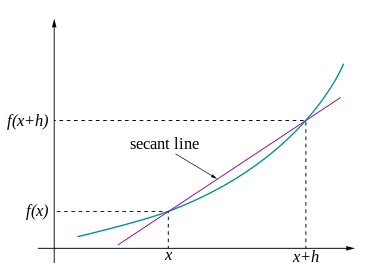
f
(
x
+
h
)
−
f
(
x
)
h
= \lim _ { h \rightarrow 0 } \frac { f ( x + h ) - f ( x ) } { h }
= h → 0 lim h f ( x + h ) − f ( x )
当极限存在就说通了。经过计算得出来的数就成了导数,实际书上或者其他地方只要能看到的,画的切线都是“最佳近似”的切线。“计算”可以精确,“画”只能最佳近似。
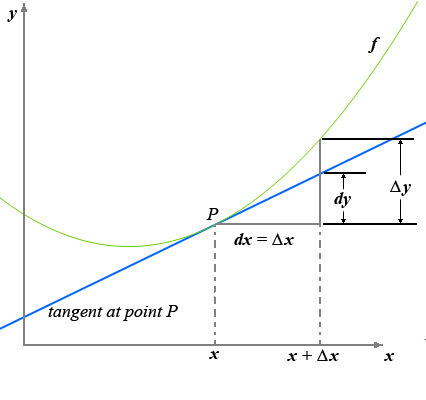
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
Δ
y
Δ
x
f ^ { \prime } ( x ) = \lim _ { \Delta x \rightarrow 0 } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } = \lim _ { \Delta x \rightarrow 0 } \frac { \Delta y } { \Delta x }
f ′ ( x ) = Δ x → 0 lim Δ x f ( x + Δ x ) − f ( x ) = Δ x → 0 lim Δ x Δ y
林群在上海交大报告《微积分降到最低点》中举了一个很简单的例子说明什么是导数
微积分之首是导数,擒贼先擒王。导数是什么?
91
10
=
9
+
0.1
\frac { 91 } { 10 } = 9 + 0.1
1 0 9 1 = 9 + 0 . 1
若四舍五入,右边剩下整数9,简化做了除法,回到
x
2
x^2
x 2
(
x
+
h
)
2
−
x
2
h
=
?
\frac { ( x + h ) ^ { 2 } - x ^ { 2 } } { h } = ?
h ( x + h ) 2 − x 2 = ?
x
x
x
h
h
h
(
x
+
h
)
2
−
x
2
h
=
2
x
+
h
\frac { ( x + h ) ^ { 2 } - x ^ { 2 } } { h } = 2 x + h
h ( x + h ) 2 − x 2 = 2 x + h
这等式是纯代数,无论
h
h
h
h
→
0
h \rightarrow 0
h → 0
2
x
+
0
2x+0
2 x + 0
x
2
x^2
x 2
(
x
2
)
′
=
2
x
\left( x ^ { 2 } \right) ^ { \prime } = 2 x
( x 2 ) ′ = 2 x
总结他的理解方式是 导数时差商的简化
字母变更下
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta(x)=\theta_0+\theta_1x
h θ ( x ) = θ 0 + θ 1 x
h 表示 hypothesis(假设),是一个函数,从x 到 y 的函数映射整个步骤
1 预测函数(Hypothesis)
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_{\theta}(x)=\theta_{0}+\theta_{1}x
h θ ( x ) = θ 0 + θ 1 x
2 参数(Parameters)
θ
0
,
θ
1
\theta_{0},\theta_{1}
θ 0 , θ 1
3 代价函数 (Cost Function),有的地方称为损失函数(Loss Function) 或者 误差函数(Error Function)
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
h
θ
x
(
i
)
−
y
(
i
)
)
2
J(\theta_{0},\theta_{1}) = \frac{1}{2m}\sum_{i=1}^{m} (h_\theta x^{(i)}-y^{(i)})^2
J ( θ 0 , θ 1 ) = 2 m 1 i = 1 ∑ m ( h θ x ( i ) − y ( i ) ) 2
4 目的(Goal)
(
θ
0
,
θ
1
)
=
min
θ
0
,
θ
1
J
(
θ
0
,
θ
1
)
(\theta_{0},\theta_{1})=\min_{\theta_{0},\theta_{1}} J(\theta_{0},\theta_{1})
( θ 0 , θ 1 ) = θ 0 , θ 1 min J ( θ 0 , θ 1 ) 可视化理解
θ
0
=
0
\theta_0=0
θ 0 = 0
#假设有三组数据,数据分别为(1,1),(2,2),(3,3)
x=np.array([1,2,3])
y=np.array([1,2,3])
#预测1
y1=0.5*x
y2=1*x
y3=-0.5*x
print( (1/(2*len(x)) )* sum(np.power(y1-y,2))) #0.58
print( (1/(2*len(x)) )* sum(np.power(y2-y,2))) #0
print( (1/(2*len(x)) )* sum(np.power(y3-y,2))) #5.25
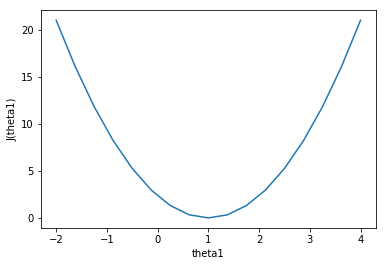
#画图 看看是J(theta1)什么样子的
#a=np.linspace(-2,2,9)#[-2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. ]
theta1=np.linspace(-2,4,17)
j=np.array([])
for i in theta1:
y_=i*x
b= (1/(2*len(x)) )* sum(np.power(y_-y,2))
j=np.append(j,b)
print(j)
plt.xlabel('theta1')
plt.ylabel('J(theta1)')
plt.plot(theta1,j)
如果有多个特征,不仅仅是人口
x
1
x_1
x 1
x
2
x_2
x 2
x
3
x_3
x 3
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
⋯
+
θ
n
x
n
=
θ
T
x
h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\dots+\theta_nx_n=\theta^Tx
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n = θ T x
θ
T
x
=
[
θ
1
θ
2
.
.
.
θ
n
]
[
x
1
x
2
.
.
.
x
n
]
=
∑
i
=
1
n
θ
i
x
i
=
h
θ
(
x
)
\theta^T x = \left[ \begin{matrix} \theta _ 1 \\\\ \theta _ 2 \\\\ ...\\\\ \theta _ n \\\\ \end{matrix} \right] \left[ \begin{matrix} x _ 1 & x _ 2 & ... & x _ n \end{matrix} \right] = \sum_{i=1}^n\theta _ i x _ i = h_\theta(x)
θ T x = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ θ 1 θ 2 . . . θ n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ [ x 1 x 2 . . . x n ] = i = 1 ∑ n θ i x i = h θ ( x )
[
1
,
2
3
,
4
5
,
6
]
T
=
[
1
,
3
,
5
2
,
4
,
6
]
{\begin{bmatrix}1,2\\3,4\\5,6\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1,3,5\\2,4,6\end{bmatrix}}
⎣ ⎡ 1 , 2 3 , 4 5 , 6 ⎦ ⎤ T = [ 1 , 3 , 5 2 , 4 , 6 ]
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
,
m
为
样
本
数
J(\theta)=\frac{1}{2m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2,\quad {m 为样本数}
J ( θ ) = 2 m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) 2 , m 为 样 本 数
矩阵形式
J
(
θ
)
=
1
2
m
(
X
θ
−
y
)
T
(
X
θ
−
y
)
J(\theta)=\frac{1}{2m}(X\theta-y)^T(X\theta-y)
J ( θ ) = 2 m 1 ( X θ − y ) T ( X θ − y ) 梯度下降
柯西将极限的定义引入了微积分,很创新。因为微积分的创造者们没有把一件事说明白,他用新的概念把这件事说明白了。问题变了,思维方式就变了,之前的人的问题是什么什么是多少,他的问题是如何定义“什么什么”的问题。他定义的框架把微积分的严谨度向前迈了一大步,所以问什么样的问题最重要。微积分的现代体系就是他建的。
数学有些地方又是借鉴物理知识,可以在后面的深度学习部分看到。从芝诺用不是数学的语言-大白话描述它,到现在都2500多年了。中国的先人们发现的什么什么定理领先西方多少多少年,到了明朝后期比较尴尬了,19世纪末期清代的李善兰把这个知识引入到中国。别人是先进的,那就无论好坏对错全盘吸收,然后持续积累改进迭代。如果后人把问题再变了,那又会离“微积分真理”又进了一步。人的语言可以表达不存在的东西,因相信而这不存在东西也就变得存在。
说梯度的时候,还得理解方向导数,偏导数。
z
=
f
(
x
,
y
)
z = f ( x , y )
z = f ( x , y )
(
x
0
,
y
0
)
(x_0,y_0)
( x 0 , y 0 )
x
x
x
f
x
′
(
x
0
,
y
0
)
=
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
,
y
0
)
−
f
(
x
0
,
y
0
)
Δ
x
f _ { x } ^ { \prime } \left( x _ { 0 } , y _ { 0 } \right) = \lim _ { \Delta x \rightarrow 0 } \frac { f \left( x _ { 0 } + \Delta x , y _ { 0 } \right) - f \left( x _ { 0 } , y _ { 0 } \right) } { \Delta x }
f x ′ ( x 0 , y 0 ) = Δ x → 0 lim Δ x f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 )
(
x
0
,
y
0
)
(x_0,y_0)
( x 0 , y 0 )
y
y
y
f
y
′
(
x
0
,
y
0
)
=
lim
Δ
y
→
0
f
(
x
0
,
y
0
+
Δ
y
)
−
f
(
x
0
,
y
0
)
Δ
y
f _ { y } ^ { \prime } \left( x _ { 0 } , y _ { 0 } \right) = \lim _ { \Delta y \rightarrow 0 } \frac { f \left( x _ { 0 } , y _ { 0 } + \Delta y \right) - f \left( x _ { 0 } , y _ { 0 } \right) } { \Delta y }
f y ′ ( x 0 , y 0 ) = Δ y → 0 lim Δ y f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 )
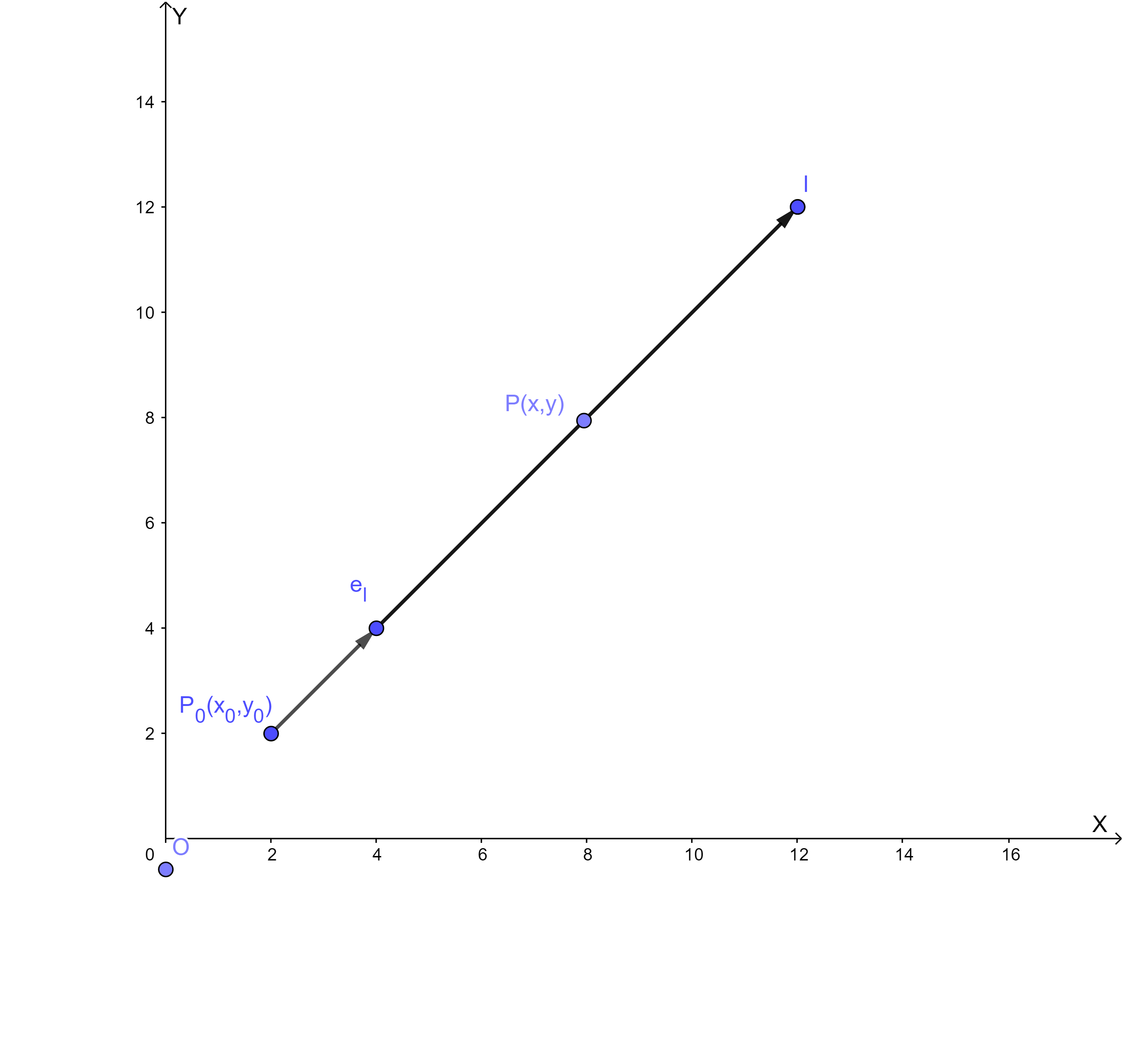
下面用数学语言来描述方向导数,用数学语言作为标杆,优点严谨,强逻辑,不产生歧义,缺点不易懂。之后我用大白话说明是什么问题。多本教科书均有定义,这里采用 同济大学《高等数学 第七版 下册》103页的《方向导数与梯度》
设
l
l
l
x
O
y
xOy
x O y
P
0
(
x
0
,
y
0
)
P_0(x_0,y_0)
P 0 ( x 0 , y 0 )
e
l
=
(
cos
α
,
cos
β
)
e_l=(\cos \alpha,\cos \beta)
e l = ( cos α , cos β )
l
l
l
l
l
l
x
=
x
0
+
t
cos
α
y
=
y
0
+
t
cos
β
t
⩾
0
\begin{array} { c } { x = x _ { 0 } + t \cos \alpha } \\ { y = y _ { 0 } + t \cos \beta } \\ { t \geqslant 0 } \end{array}
x = x 0 + t cos α y = y 0 + t cos β t ⩾ 0
设函数
z
=
f
(
x
,
y
)
z=f(x,y)
z = f ( x , y )
P
0
(
x
0
,
y
0
)
P_0(x_0,y_0)
P 0 ( x 0 , y 0 )
U
(
P
0
)
U(P_0)
U ( P 0 )
P
(
x
0
+
t
c
o
s
α
,
y
0
+
t
c
o
s
β
)
P(x_{0}+tcos\alpha,y_{0}+tcos\beta)
P ( x 0 + t c o s α , y 0 + t c o s β )
l
l
l
P
∈
U
(
P
0
)
P\in U(P_{0})
P ∈ U ( P 0 )
f
(
x
0
+
t
c
o
s
α
,
y
0
+
t
c
o
s
β
)
−
f
(
x
0
,
y
0
)
{f(x_{0}+tcos\alpha,y_{0}+tcos\beta)-f(x_{0},y_{0})}
f ( x 0 + t c o s α , y 0 + t c o s β ) − f ( x 0 , y 0 )
P
P
P
P
0
P_0
P 0
∣
P
P
0
∣
=
t
|PP_0|=t
∣ P P 0 ∣ = t
f
(
x
0
+
t
c
o
s
α
,
y
0
+
t
c
o
s
β
)
−
f
(
x
0
,
y
0
)
t
\frac{f(x_{0}+tcos\alpha,y_{0}+tcos\beta)-f(x_{0},y_{0})}{t}
t f ( x 0 + t c o s α , y 0 + t c o s β ) − f ( x 0 , y 0 )
当
P
P
P
l
l
l
P
0
(
即
t
→
0
+
)
P_{0}(即t\rightarrow0^{+})
P 0 ( 即 t → 0 + )
f
(
x
,
y
)
f(x,y)
f ( x , y )
P
0
P_0
P 0
∂
f
∂
l
∣
(
x
0
,
y
0
)
=
lim
t
→
0
+
f
(
x
0
+
t
c
o
s
α
,
y
0
+
t
c
o
s
β
)
−
f
(
x
0
,
y
0
)
t
‘
\frac{\partial f}{\partial l} \mid_{(x_{0},y_{0})}=\lim_{t \rightarrow 0^{+}}\frac{f(x_{0}+tcos\alpha,y_{0}+tcos\beta)-f(x_{0},y_{0})}{t}`
∂ l ∂ f ∣ ( x 0 , y 0 ) = t → 0 + lim t f ( x 0 + t c o s α , y 0 + t c o s β ) − f ( x 0 , y 0 ) ‘
图片来自wiki
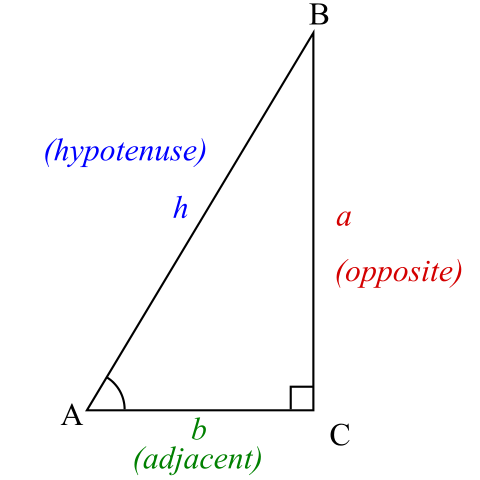
直角三角形的两条直角边长分别是a和b,斜边长是h,数学语言是
a
2
+
b
2
=
h
2
a ^ { 2 } + b ^ { 2 } = h ^ { 2 }
a 2 + b 2 = h 2
sin
cos
\sin \cos
sin cos
sin
A
=
opposite(对边)
hypotenuse(斜边)
\sin A = \frac { \text { opposite(对边) } } { \text { hypotenuse(斜边) } }
sin A = hypotenuse( 斜边 ) opposite( 对边 )
cos
A
=
adjacent(邻边)
hypotenuse(斜边)
\cos A = \frac { \text { adjacent(邻边) } } { \text { hypotenuse(斜边) } }
cos A = hypotenuse( 斜边 ) adjacent( 邻边 )
tan
A
=
sin
A
cos
A
\tan A = \frac { \sin A } { \cos A }
tan A = cos A sin A
单位向量
e
l
=
(
cos
α
,
cos
β
)
e_l=(\cos \alpha,\cos \beta)
e l = ( cos α , cos β )
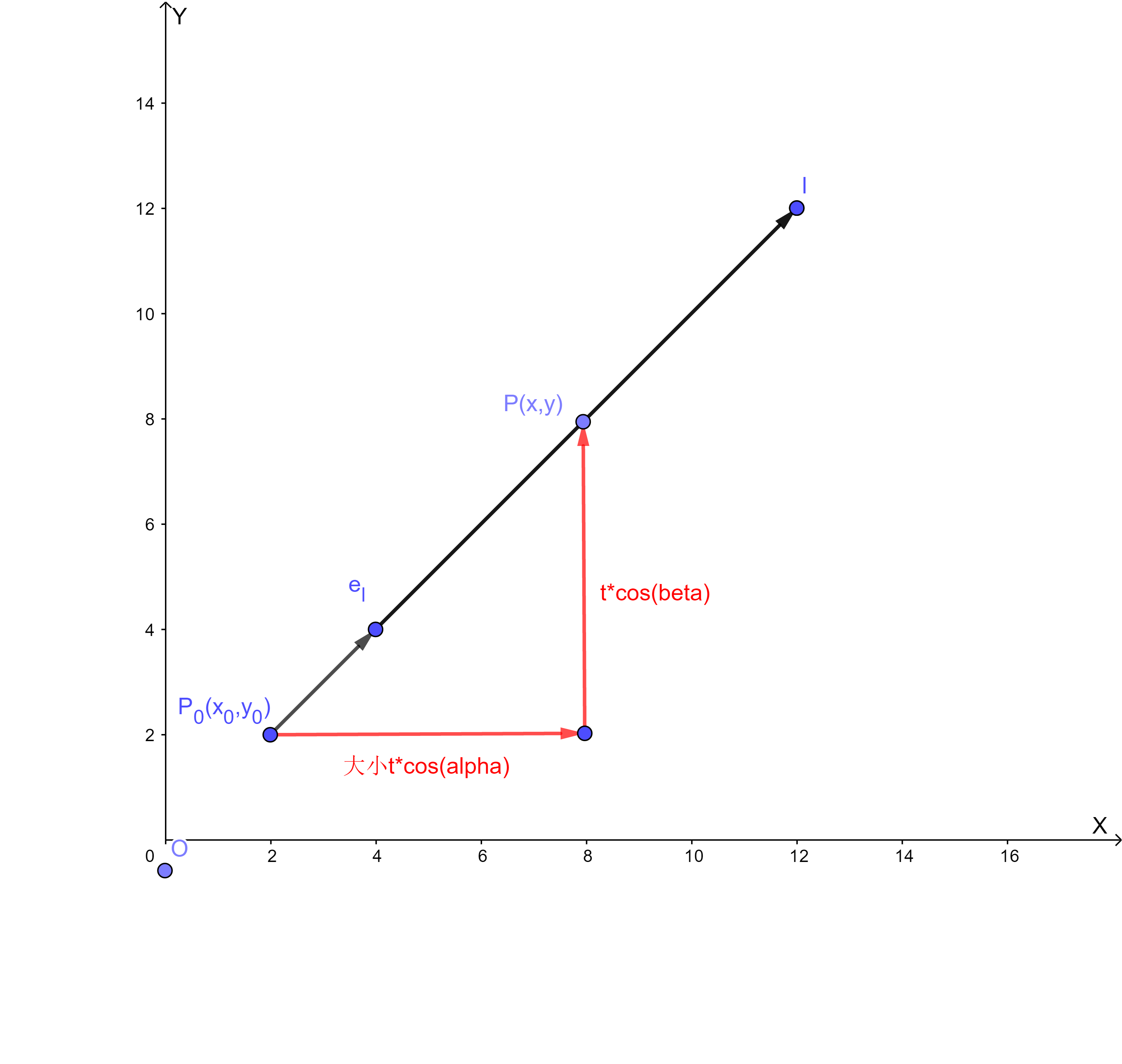
这就是上面提到的单位向量
e
l
e_l
e l
(
cos
α
,
cos
β
)
(\cos \alpha,\cos \beta)
( cos α , cos β )
e
l
e_l
e l
t
∗
c
o
s
(
a
l
p
h
a
)
=
t
∗
c
o
s
(
α
)
=
Δ
x
t*cos(alpha)=t*cos(\alpha)=\Delta x
t ∗ c o s ( a l p h a ) = t ∗ c o s ( α ) = Δ x
t
∗
c
o
s
(
b
e
t
a
)
=
t
∗
c
o
s
(
β
)
=
Δ
y
t*cos(beta)=t*cos(\beta)=\Delta y
t ∗ c o s ( b e t a ) = t ∗ c o s ( β ) = Δ y
ρ
=
∣
P
P
0
∣
=
Δ
x
2
+
Δ
y
2
Δ
z
=
f
(
x
+
Δ
x
,
y
+
Δ
y
)
−
f
(
x
,
y
)
∂
f
∂
l
=
lim
ρ
→
0
f
(
x
+
Δ
x
,
y
+
Δ
y
)
−
f
(
x
,
y
)
ρ
\rho = \left| P P _ { 0 } \right| = \sqrt { \Delta x ^ { 2 } + \Delta y ^ { 2 } } \ \\ \Delta z = f ( x + \Delta x , y + \Delta y ) - f ( x , y ) \\ \frac { \partial f } { \partial l } = \lim _ { \rho \rightarrow 0 } \frac { f ( x + \Delta x , y + \Delta y ) - f ( x , y ) } { \rho }
ρ = ∣ P P 0 ∣ = Δ x 2 + Δ y 2
Δ z = f ( x + Δ x , y + Δ y ) − f ( x , y ) ∂ l ∂ f = ρ → 0 lim ρ f ( x + Δ x , y + Δ y ) − f ( x , y )
方向导数就像我们给地球定义了东西南北,正南正北刮的就像偏导数,地球上的风是可以按照任意方向刮的,就像方向导数。
t
a
n
6
0
∘
=
3
tan60 ^ { \circ }=\sqrt { 3 }
t a n 6 0 ∘ = 3
t
a
n
4
5
∘
=
1
tan45 ^ { \circ }=1
t a n 4 5 ∘ = 1
t
a
n
3
0
∘
=
3
3
tan30 ^ { \circ }=\frac { \sqrt { 3 } } { 3 }
t a n 3 0 ∘ = 3 3
t
a
n
0
∘
=
0
tan0 ^ { \circ }=0
t a n 0 ∘ = 0
梯度
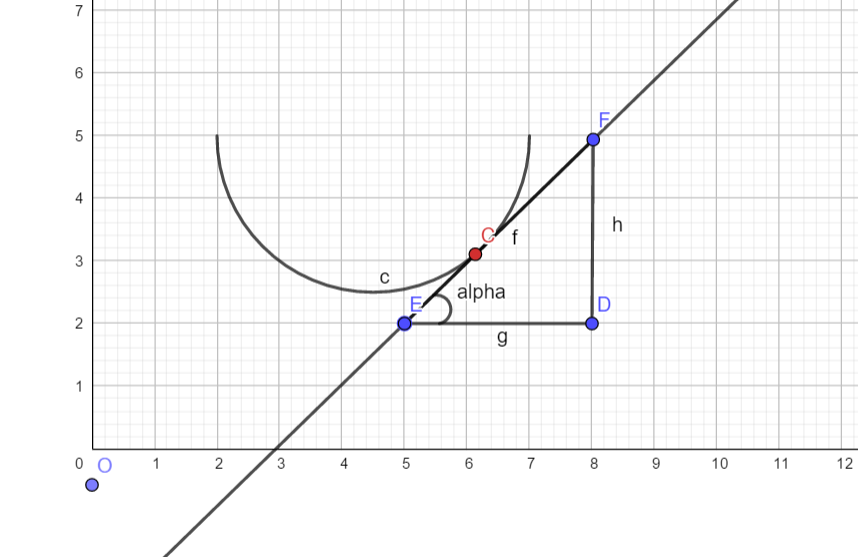
解释什么是向量的模?
A
(
x
1
,
y
1
)
B
(
x
2
,
y
2
)
A \left( x _ { 1 } , y _ { 1 } \right) B \left( x _ { 2 } , y _ { 2 } \right)
A ( x 1 , y 1 ) B ( x 2 , y 2 )
∣
A
B
⃗
∣
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
| \vec { \mathbf { A B } } | = \sqrt { \left( \boldsymbol { x } _ { 2 } - \boldsymbol { x } _ { \mathbf { 1 } } \right) ^ { 2 } + \left( \boldsymbol { y } _ { 2 } - \boldsymbol { y } _ { \mathbf { 1 } } \right) ^ { 2 } }
∣ A B
∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2
欧式距离 ,在机器学习中叫2-范数
∣
a
⃗
∣
=
(
x
,
y
)
| \vec { \boldsymbol { a } } | =( x , y )
∣ a
∣ = ( x , y )
∣
a
⃗
∣
=
x
2
+
y
2
| \vec { \boldsymbol { a } } | = \sqrt { \boldsymbol { x } ^ { 2 } + \boldsymbol { y } ^ { 2 } }
∣ a
∣ = x 2 + y 2
∇
f
(
x
0
,
y
0
)
\nabla f(x_0,y_0)
∇ f ( x 0 , y 0 )
gradf
(
x
,
y
)
=
(
∂
f
∂
x
)
2
+
(
∂
f
∂
y
)
2
\operatorname { grad f } ( x , y ) = \sqrt { \left( \frac { \partial f } { \partial x } \right) ^ { 2 } + \left( \frac { \partial f } { \partial y } \right) ^ { 2 } }
g r a d f ( x , y ) = ( ∂ x ∂ f ) 2 + ( ∂ y ∂ f ) 2
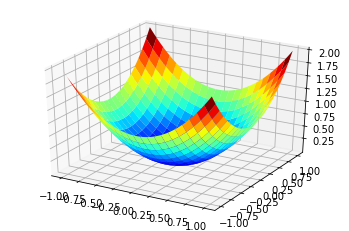
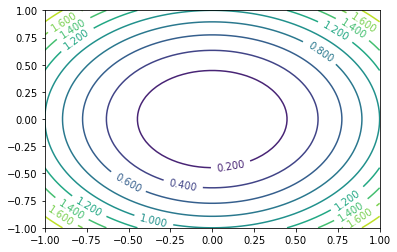
以二元z=f(x,y)这样的曲面用等值线表示
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return (x**2+y**2)
n = 64
x = np.linspace(-1, 1, n)
y = np.linspace(-1, 1, n)
#画原图
fig = plt.figure()
x1,y1 = np.meshgrid(x,y)
pic1=fig.add_subplot(111,projection='3d')
pic1.plot_surface(x1,y1,f(x1,y1),rstride=3,cstride=3,cmap=plt.cm.jet)
plt.show()
#画等值线
fig = plt.figure()
x2, y2 = np.meshgrid(x, y)
t = plt.contour(x2, y2, f(x2, y2), 10)
plt.clabel(t, inline=True, fontsize=10)
plt.show()
原图等值线
泰勒公式
用切线近似的表示一个弧
近似公式
f
(
x
)
≈
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
f ( x ) \approx f \left( x _ { 0 } \right) + f ^ { \prime } \left( x _ { 0 } \right) \left( x - x _ { 0 } \right)
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 )
f
(
x
)
≈
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
+
a
2
(
x
−
x
0
)
2
f ( x ) \approx f \left( x _ { 0 } \right) + f ^ { \prime } \left( x _ { 0 } \right) \left( x - x _ { 0 } \right) + a _ { 2 } \left( x - x _ { 0 } \right) ^ { 2 }
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + a 2 ( x − x 0 ) 2
n次多项式近似的表示f(x)
P
(
x
)
=
a
0
+
a
1
(
x
−
x
0
)
+
a
2
(
x
−
x
0
)
2
+
⋯
+
a
n
(
x
−
x
0
)
n
P ( x ) = a _ { 0 } + a _ { 1 } \left( x - x _ { 0 } \right) + a _ { 2 } \left( x - x _ { 0 } \right) ^ { 2 } + \cdots + a _ { n } \left( x - x _ { 0 } \right) ^ { n }
P ( x ) = a 0 + a 1 ( x − x 0 ) + a 2 ( x − x 0 ) 2 + ⋯ + a n ( x − x 0 ) n
P
n
(
x
)
=
P
(
x
0
)
+
P
′
(
x
0
)
(
x
−
x
0
)
+
P
′
′
(
x
0
)
2
!
(
x
−
x
0
)
2
+
⋯
+
P
(
n
)
(
x
0
)
n
!
(
x
−
x
0
)
n
\begin{aligned} P _ { n } ( x ) = & P \left( x _ { 0 } \right) + P ^ { \prime } \left( x _ { 0 } \right) \left( x - x _ { 0 } \right) + \frac { P ^ { \prime \prime } \left( x _ { 0 } \right) } { 2 ! } \left( x - x _ { 0 } \right) ^ { 2 } + \cdots + \frac { P ^ { ( n ) } \left( x _ { 0 } \right) } { n ! } \left( x - x _ { 0 } \right) ^ { n } \end{aligned}
P n ( x ) = P ( x 0 ) + P ′ ( x 0 ) ( x − x 0 ) + 2 ! P ′ ′ ( x 0 ) ( x − x 0 ) 2 + ⋯ + n ! P ( n ) ( x 0 ) ( x − x 0 ) n
算法
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
α
是
学
习
率
\theta_j := \theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta) \quad {\alpha 是学习率}
θ j : = θ j − α ∂ θ j ∂ J ( θ ) α 是 学 习 率
r
e
p
e
a
t
u
n
t
i
l
c
o
n
v
e
r
g
e
n
c
e
{
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
0
,
θ
1
)
}
\begin{aligned} & repeat\ until\ convergence \{ \\ & \theta _ { j } : = \theta _ { j } - \alpha \frac { \partial } { \partial \theta _ { j } } J \left( \theta _ { 0 } , \theta _ { 1 } \right) \\ &\}\\ \end{aligned}
r e p e a t u n t i l c o n v e r g e n c e { θ j : = θ j − α ∂ θ j ∂ J ( θ 0 , θ 1 ) }
求代价函数的导数
∂
∂
θ
j
J
(
θ
0
θ
1
)
=
∂
∂
θ
j
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
\frac { \partial } { \partial \theta _ { j } } J \left( \theta _ { 0 } \theta _ { 1 } \right) = \frac { \partial } { \partial \theta _ { j } } \frac { 1 } { 2 m } \sum _ { i = 1 } ^ { m } \left( h _ { \theta } \left( x ^ { ( i ) } \right) - y ^ { ( i ) } \right) ^ { 2 }
∂ θ j ∂ J ( θ 0 θ 1 ) = ∂ θ j ∂ 2 m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) 2
j=0
∂
∂
θ
0
J
(
θ
0
θ
1
)
=
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
\frac { \partial } { \partial \theta _ { 0 } } J \left( \theta _ { 0 } \theta _ { 1 } \right) = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left( h _ { \theta } \left( x ^ { ( i ) } \right) - y ^ { ( i ) } \right)
∂ θ 0 ∂ J ( θ 0 θ 1 ) = m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) )
∂
∂
θ
1
J
(
θ
0
θ
1
)
=
1
m
∑
i
=
1
m
(
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
⋅
x
(
i
)
)
\frac { \partial } { \partial \theta _ { 1 } } J \left( \theta _ { 0 } \theta _ { 1 } \right) = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left( \left( h _ { \theta } \left( x ^ { ( i ) } \right) - y ^ { ( i ) } \right) \cdot x ^ { ( i ) } \right)
∂ θ 1 ∂ J ( θ 0 θ 1 ) = m 1 i = 1 ∑ m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) )
算法变更为
$$
\end{aligned}
import matplotlib.pyplot as plt
import numpy as np
import matplotlib
zhfont = matplotlib.font_manager.FontProperties(fname='C:\Windows\Fonts\simsun.ttc')
#theta0需要和1相乘,所以加了一列1
def getDataSet():
dataset_x = np.array([[1,1,1,1],[1,2,3,4]]).T
y = np.array([[6],[5],[7],[10]])
print(dataset_x)
print(y)
return dataset_x,y
def getCost(dataset_x, y ,theta):
temp = np.power((dataset_x*theta.T) - y,2)
return 1/(2*len(dataset_x)*sum(temp))
'''
theta: 需要更新的theta值
alpha: 学习速率
iters:迭代次数
'''
def gradientDescent(dataset_x, y ,theta, alpha, iters):
temp = np.mat(np.zeros(theta.shape))
cost = np.zeros(iters)
parameters = int (theta.shape[1])
for i in range(iters):
error = dataset_x*theta.T - y
for j in range(parameters):
term = np.multiply(error,dataset_x[:,j])
temp[0,j] = theta[0,j] - alpha / len(dataset_x) * sum(term)
theta = temp
cost[i] = getCost(dataset_x,y,theta)
return theta,cost
if __name__ == '__main__':
dataset_x,y = getDataSet()
alpha = 0.01
theta = np.mat(np.array([0,0]))
print(theta)
dataset_x = np.mat(dataset_x)
y = np.mat(y)
print(dataset_x)
print(y)
iters = 100
theta,cost = gradientDescent(dataset_x,y,theta,alpha,iters)
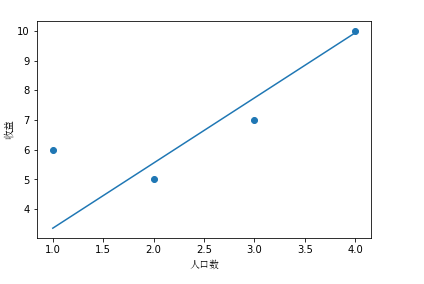
x = np.linspace(dataset_x[:,1].min(),dataset_x[:,1].max(),100)
h = theta[0,0] + (theta[0,1] * x)
plt.scatter(np.array(dataset_x[:,1]),np.array(y[:,0]))
plt.xlabel('人口数',fontproperties=zhfont)
plt.ylabel('收益',fontproperties=zhfont)
plt.plot(x,h)
L1-norm(LASSO回归)
J
(
θ
)
=
1
2
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
(
i
)
)
2
+
λ
∑
j
=
1
n
∣
θ
j
∣
λ
>
0
J(\theta) = \frac{1}{2}\sum^m_{i=1}(h_{\theta}(x^{i}) - y^{(i)})^2 + \lambda\sum^n_{j=1} |\theta_j| \ \ \ \lambda > 0
J ( θ ) = 2 1 i = 1 ∑ m ( h θ ( x i ) − y ( i ) ) 2 + λ j = 1 ∑ n ∣ θ j ∣ λ > 0 L2-norm(Ridge回归,岭回归)
J
(
θ
)
=
1
2
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
(
i
)
)
2
+
λ
∑
j
=
1
n
θ
j
2
λ
>
0
J(\theta) = \frac{1}{2}\sum^m_{i=1}(h_{\theta}(x^{i}) - y^{(i)})^2 + \lambda\sum^n_{j=1} \theta_j^2 \ \ \ \lambda > 0
J ( θ ) = 2 1 i = 1 ∑ m ( h θ ( x i ) − y ( i ) ) 2 + λ j = 1 ∑ n θ j 2 λ > 0
同时引入L1-norm和L2-norm(弹性网络ElasitcNet)
J
(
θ
)
=
1
2
∑
i
=
1
m
(
h
θ
(
x
i
−
y
(
i
)
)
)
2
+
λ
(
p
∑
j
=
1
n
θ
j
2
+
(
1
−
p
)
∑
j
=
1
n
∣
θ
j
∣
)
λ
>
0
&
&
p
∈
[
0
,
1
]
J(\theta) = \frac{1}{2}\sum^m_{i=1}(h_{\theta}(x^{i} - y^{(i)}))^2 + \lambda(p\sum^n_{j=1} \theta_j^2 +(1-p)\sum^n_{j=1} |\theta_j| )\ \ \ \lambda > 0 \&\& p \in [0,1]
J ( θ ) = 2 1 i = 1 ∑ m ( h θ ( x i − y ( i ) ) ) 2 + λ ( p j = 1 ∑ n θ j 2 + ( 1 − p ) j = 1 ∑ n ∣ θ j ∣ ) λ > 0 & & p ∈ [ 0 , 1 ]