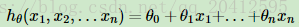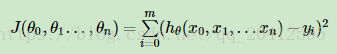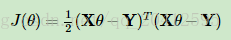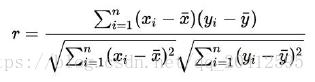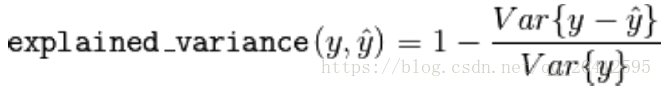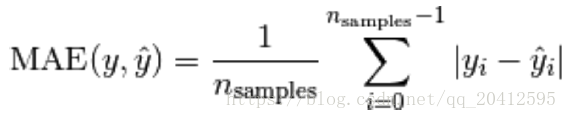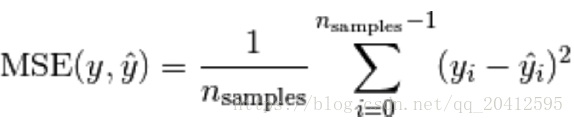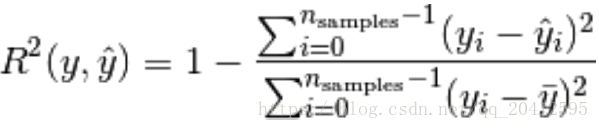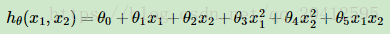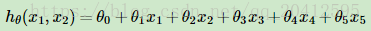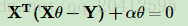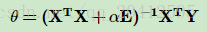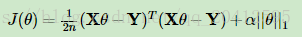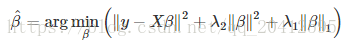【机器学习算法】【8】--多元线性回归分析理论详解

前言：当影响因变量的因素是多个时候，这种一个变量同时与多个变量的回归问题就是多元回归，分为：多元线性回归和多元非线性回归。线性回归(Linear regressions)和逻辑回归(Logistic regressions)是人们学习算法的第一个预测模型。因此它们很常见，还有许多分析人员认为它们是仅有的回归模型，部分分析师认为它们是所有回归模型中最重要的。事实上有无数的回归模型都能被使用，每种形式的回归模型都有它独特且重要的应用场景。在这篇文章里以简单的方式解释最常用的7种回归模型，通过这篇文章，对回归模型有一种广泛性的了解，取而代之的是希望能在每个场景合适的使用linear / logistic regression。

一、回归分析(Regression Analysis)定义与分类

回归分析（Regression Analysis）是一种统计学上分析数据的方法，目的在于了解两个或多个变数间是否相关、相关方向与强度，并建立数学模型以便观察特定变数来预测研究者感兴趣的变数。更具体的来说，回归分析可以帮助人们了解在只有一个自变量变化时因变量的变化量。一般来说，通过回归分析我们可以由给出的自变量估计因变量的条件期望。回归分析是建立因变数 Y（或称依变数，反应变数）与自变数 X（或称独变数，解释变数）之间关系的模型。

回归分析的主要算法包括：

线性回归(Linear Regression)
逻辑回归（Logistic regressions）
多项式回归(Polynomial Regression)
逐步回归(Step Regression)
岭回归(Ridge Regression)
套索回归(Lasso Regression)
弹性网回归(ElasticNet)

为什么使用回归分析？

如上所述，回归分析是评估两个或更多变量之间的关系。让我们使用一个简单的例子进行理解：

你想基于当前的经济状况去评估公司的销售额的增长，公司最近的数据表明在当前的经济条件下出现2到5倍的增长，利用这个发现，我们能基于当前或过去的信息来预测公司未来的销售情况。

这有使用回归分析的几点好处：
1.它表明了因变量和独立变量之间的重要关系；
2.它表明的是多个独立变量对因变量影响的强度。

回归分析还使我们能比较变量在不同程度上影响，如价格变动对促销活动的影响。这样有利于市场研究员／数据分析师／数据科学家在建立模型的时候排除并评估出最好的变量。

二、七种回归算法

1）线性回归(Linear Regression)

这里就忽略一元线性回归了，直接讲多元线性回归，原理都是一样的。对于n维特征的样本数据，如果我们决定使用线性回归，那么对应的模型是这样的：

这个表示可以简化，我们增加一个特征x0=1，这样

进一步用矩阵形式表达更加简洁如下： $h_{\theta }(X)=X\cdot \theta$

其中，假设函数 $h_{\theta }(X)$ 为mx1的向量,θ为nx1的向量，里面有n个代数法的模型参数。X为mxn维的矩阵。m代表样本的个数，n代表样本的特征数。

得到了模型，我们需要求出需要的损失函数，一般线性回归我们用均方误差作为损失函数。损失函数的代数法表示如下：

进一步用矩阵形式表达损失函数：

我们常用的有两种方法来求损失函数最小化时候的θθ参数：一种是梯度下降法，一种是最小二乘法。

如果采用梯度下降法，则θ的迭代公式是这样的：

$\theta =\theta -\alpha X^{T}(\theta X-Y)$

如果采用最小二乘法，则θ的结果公式如下：

$\theta =(X^{T}X)^{-1}X^{T}Y$

当然线性回归，还有其他的常用算法，比如牛顿法和拟牛顿法，这里不详细描述。

注意，在业务上对数据的拟合，要注意多重共线性的问题以及对回归方程的检验。

回归方程的拟合优度：

多重判定系数：(Multiple coefficient of determination)

线性关系的检验：统计学中F统计量（还有t检验量）

步骤：
（1）：提出假设

（2）：计算检验的统计量F.

（2）’：计算检验的统计量t

（3）：作出统计决策。

多重共线性----这是回归任务中比较常见的额问题，要引起高度重视

在多元线性回归模型经典假设中，其重要假定之一是回归模型的解释变量之间不存在线性关系，也就是说，解释变量X1，X2，...，Xk中的任何一个都不能是其他解释变量的线性组合。如果违背这一假定，即线性回归模型中某一个解释变量与其他解释变量间存在线性关系，就称线性回归模型中存在多重共线性。多重共线性违背了解释变量间不相关的古典假设，将给普通最小二乘法带来严重后果。

造成多重共线性的原因有一下几种：

解释变量都享有共同的时间趋势
一个解释变量是另一个的滞后，二者往往遵循一个趋势
由于数据收集的基础不够宽，某些解释变量可能会一起变动
某些解释变量间存在某种近似的线性关系

判别：

回归系数的正负号与预期的相反
某些重要的解释变量t值低，而R方不低
当一不太重要的解释变量被删除后，回归结果显著变化
模型中各对自变量之间显著相关
容忍度(tolerance) 与方差扩大因子(variance inflation factor, VIF).

容忍度：某个变量的容忍度等于 1 减去该自变量为因变量而其他k−1个自变量为预测变量时所得到的线性回归模型的判定系数。即1−R2i。容忍度越小，多重共线性越严重。通常认为容忍度小于 0.1 时，存在严重的多重共线性。
方差扩大因子：容忍度的倒数。因此，VIF越大，多重共线性越严重，一般认为VIF的值大于10时，存在严重的多重共线性。

检验:

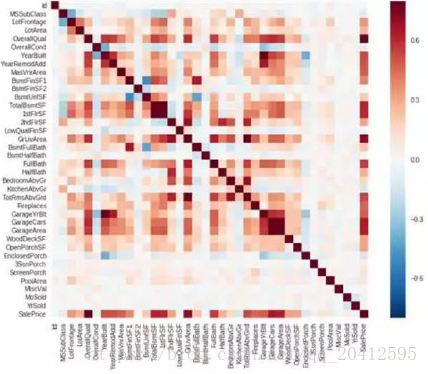
相关性分析，相关系数高于0.8，表明存在多重共线性；但相关系数低，并不能表示不存在多重共线性
VIF检验
条件系数检验

对X变量探索两两之间的相关性（相关矩阵）

这里在顺带总结一下相关分析的问题：

相关分析与回归分析都是研究变量相互关系的分析方法
相关分析是回归分析的基础和前提，而回归分析则是认识变量之间相关程度的具体形式。

根据相关关系的方向划分：正相关和负相关
根据相互关系的表现形式划分：线性相关、非线性相关、不相关

根据相互关系的强弱划分：强相关、弱相关

线性相关性度量：皮尔逊相关系数

　皮尔森相关系数是一种最简单的，能帮助理解特征和响应变量之间关系的方法，该方法衡量的是变量之间的线性相关性，结果的取值区间为[-1，1]，-1表示完全的负相关，+1表示完全的正相关，0表示没有线性相关。

Pearson Correlation速度快、易于计算，经常在拿到数据(经过清洗和特征提取之后的)之后第一时间就执行。Scipy的 pearsonr 方法能够同时计算相关系数和p-value.

Pearson相关系数的一个明显缺陷是，作为特征排序机制，他只对线性关系敏感。如果关系是非线性的，即便两个变量具有一一对应的关系，Pearson相关性也可能会接近0。例如：

x = np.random.uniform(-1, 1, 100000)
print pearsonr(x, x**2)[0]
-0.00230804707612

另外，如果仅仅根据相关系数这个值来判断的话，有时候会具有很强的误导性，如 Anscombe’s quartet ，最好把数据可视化出来，以免得出错误的结论。

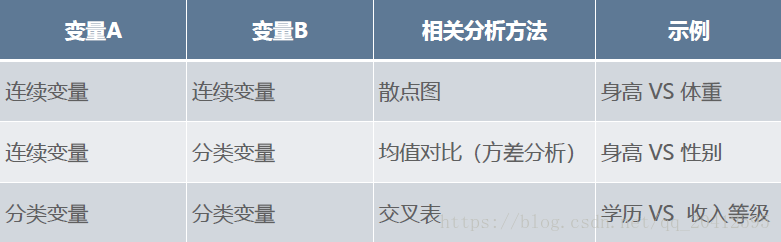
不同类型的变量的相关分析方法也不同

常用的回归模型评估指标

解释方差（ Explained variance score）
绝对平均误差（Mean absolute error）
均方误差（Mean squared error）
决定系数（R² score）

#解释方差（ Explained variance score）
from sklearn.metrics import explained_variance_score
explained_variance_score(y_true, y_pred)

#绝对平均误差（Mean absolute error）
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_true, y_pred)

#均方误差（Mean squared error）
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred)

#决定系数（R² score）
from sklearn.metrics import r2_score
r2_score(y_true, y_pred)

解决方法：参考博文

增加数据(这个在实际中难度较大)
对模型施加某些约束条件
删除一个或几个共线变量（常用的方法）
将模型适当变形，改变解释变量的形式， 改变解释变量的形式是解决多重共线性的一种简易方法，例如对于横截面数据采用相对数变量，对于时间序列数据采用增量型变量。；
主成分回归：主成分分析作为多元统计分析的一种常用方法在处理多变量问题时具有其一定的优越性，其降维的优势是明显的，主成分回归方法对于一般的多重共线性问题还是适用的，尤其是对共线性较强的变量之间。（PCA之后，结果可能会变好，但模型此时已经不好做出解释了）
逐步回归分析：逐步回归（Stepwise Regression）是一种常用的消除多重共线性、选取“最优”回归方程的方法。（下面会讲到）

sklearn中线性回归的参数：

class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)

Parameters:

Parameters:	fit_intercept : boolean, optional, default True whether to calculate the intercept for this model. If set to False, no intercept will be used in calculations (e.g. data is expected to be already centered). normalize : boolean, optional, default False This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use `sklearn.preprocessing.StandardScaler` before calling `fit` on an estimator with `normalize=False`. copy_X : boolean, optional, default True If True, X will be copied; else, it may be overwritten. n_jobs : int, optional, default 1 The number of jobs to use for the computation. If -1 all CPUs are used. This will only provide speedup for n_targets > 1 and sufficient large problems.
Attributes:	coef_ : array, shape (n_features, ) or (n_targets, n_features) Estimated coefficients for the linear regression problem. If multiple targets are passed during the fit (y 2D), this is a 2D array of shape (n_targets, n_features), while if only one target is passed, this is a 1D array of length n_features. intercept_ : array Independent term in the linear model.

fit_intercept : boolean, optional, default True

whether to calculate the intercept for this model. If set to False, no intercept will be used in calculations (e.g. data is expected to be already centered).

normalize : boolean, optional, default False

This parameter is ignored when fit_intercept is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use sklearn.preprocessing.StandardScaler before calling fit on an estimator with normalize=False.

copy_X : boolean, optional, default True

If True, X will be copied; else, it may be overwritten.

n_jobs : int, optional, default 1

The number of jobs to use for the computation. If -1 all CPUs are used. This will only provide speedup for n_targets > 1 and sufficient large problems.

Attributes:

coef_ : array, shape (n_features, ) or (n_targets, n_features)

Estimated coefficients for the linear regression problem. If multiple targets are passed during the fit (y 2D), this is a 2D array of shape (n_targets, n_features), while if only one target is passed, this is a 1D array of length n_features.

intercept_ : array

Independent term in the linear model.

2）逻辑回归（Logistic regressions）

这里不做过多阐述，详见机器学习算法系列

3）多项式回归(Polynomial Regression)

多项式回归是线性回归的推广：

如果这里不仅仅是x的一次方，比如增加二次方，那么模型就变成了多项式回归。这里写一个只有两个特征的p次方多项式回归的模型：

我们令 $x_{0}=1,x_{1}=x_{1},x_{2}=x_{2},x_{3}=x_{1}^{2},x_{4}=x_{2}^{2},x_{5}=x_{1}x_{2}$ ,这样我们就得到了下式：

可以发现，我们又重新回到了线性回归，这是一个五元线性回归，可以用线性回归的方法来完成算法。对于每个二元样本特征(x1,x2),我们得到一个五元样本特征 $(1,x_{1},x_{2},x_{1}^{2},x_{2}^{2},x_{1}x_{2})$ ，这其中包含着映射函数的过程，这里不作出过深的阐述了，通过这个改进的五元样本特征，我们重新把不是线性回归的函数变回线性回归。

附注：线性回归的推广还有另一种形式

上面是我们对样本特征端做了推广，这里我们对于特征y做推广。比如我们的输出Y不满足和X的线性关系，但是lnY 和X满足线性关系，模型函数如下： $lny=X\theta$

注意，多项式回归sklearn中没有现成的算法可以调用，但我们理解了多项式回归的原理之后，是可以分步来操作的

Python中的多项式回归实现

1.第一步--特征转换（sklearn中有现成的算法）：先构造x特征的多项式组合：组合前x1,x2，设置degree（例如2），组合
后的特征： $(1,x_{1},x_{2},x_{1}^{2},x_{2}^{2},x_{1}x_{2})$

在机器学习中，通过增加一些输入数据的非线性特征来增加模型的复杂度通常是有效的。一个简单通用的办法是使用多项式特征，这可以获得特征的更高维度和互相间关系的项。这在 PolynomialFeatures 中实现:

class sklearn.preprocessing.PolynomialFeatures(degree=2, interaction_only=False, include_bias=True)

>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X                                                 
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)                             
array([[  1.,   0.,   1.,   0.,   0.,   1.],
       [  1.,   2.,   3.,   4.,   6.,   9.],
       [  1.,   4.,   5.,  16.,  20.,  25.]])

2.第二步：调用线性回归算法针对组合特征构建回归模型（sklearn中有现成的算法）

sklearn.linear_model.LinearRegression，直接用模型拟合转换后的数据

4)逐步回归(Step Regression)

是一种多元回归模型进行变量筛选的方法，筛选尽量少的变量来获得最大化预测能力。与平时所说的 regression analysis 不太相同，stepwise regression 可以算是一种 feature extraction 的方法。

有三种方法:

向前选择法
向后剔除法
逐步回归法

向前选择从零模型（即只含常数项的模型）出发，每一步向模型中增加一个X变量：

首先选取一个X变量，它与Y变量的相关系数的绝对值最大。
其次，在模型中增加一个X变量，使得增加的X变量具有最大的F统计量值。
依次下去，直到某一步，若尚未在模型中的每一个X变量对应的F统计量值都小于某一个预先给定的值，则停止X变量选择过程

向后法和向前法实施过程正好相反。它是从全模型（即包含所有自变量的模型）出发，每一步从模型中剔除一个变量：

选择当前模型中的所有X变量对应的F统计量最小的那个，然后剔除掉
停止准则是：若在某一步，在当前模型中的每一个X变量对应的F统计量值都大于某个预先给定的临界值则停止剔除过程。

逐步回归是上述两种方法的结合：

假设利用向前法已经选择了两个X变量进入当前模型。下一步不是继续使用向前法选择尚未在模型中的变量，而是对当前模型中的X变量做检验，看看当前模型中的每一个自变量是否显著，不显著的变量从模型中剔除（同向后剔除法）（这样做的原因是，向前法第二步选入的变量可能使第一步选入的变量变得不再显著）。
继续使用向前法选择尚未在模型中的X变量，然后再用向后法对当前模型做检验...依次下去。停止准则是：若在某一步，当前模型中的每一个变量都是显著的，而尚未在模型中的每一个变量都是不显著的。

我记得，逐步回归在《机器学习实战》中有讲到，并附有案例代码，这里我就略过了。感兴趣的话也可以自己上网查一下。

5)岭回归(Ridge Regression)

为了防止模型的过拟合，我们在建立线性模型的时候经常需要加入正则化项。一般有L1正则化和L2正则化。

线性回归的L2正则化通常称为Ridge回归，它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项。具体Ridge回归的损失函数表达式如下：

其中α为常数系数，需要进行调优。 $||\theta||_{2}^{2}$ 为L2范数。Ridge回归在不抛弃任何一个特征的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但和Lasso回归比，这会使得模型的特征留的特别多，模型解释性差。

Ridge回归的求解比较简单，一般用最小二乘法。这里给出用最小二乘法的矩阵推导形式，和普通线性回归类似。

令J(θ)的导数为0，得到下式：

整理即可得到最后的θθ的结果：

Ridge回归是当数据受多重共线性（自相关变量高度相关）时常使用的技术。

要点
* 该回归的假设与最小二乘回归相同，除非不假设数据集正态性；
* 它收缩系数的值，但不会达到零，这表明没有特征选择特征；
* 这是一个正则化方法，并使用l2正则化。

class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)¶

6)套索回归(Lasso Regression)

线性回归的L1正则化通常称为Lasso回归，它和一般线性回归的区别是在损失函数上增加了一个L1正则化的项，L1正则化的项有一个常数系数α来调节损失函数的均方差项和正则化项的权重，具体Lasso回归的损失函数表达式如下：

Lasso回归可以使得一些特征的系数变小，甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能力。Lasso回归的求解办法一般有坐标轴下降法（coordinate descent）和最小角回归法（ Least Angle Regression）.

要点
* 该回归的假设与最小二乘回归相同，除非不假设正态性；
* 它将系数收缩为零（正好为零），这有助于特征选择；
* 这是一个正则化方法，使用l1正则化；
* 如果一批预测变量是高度相关，则Lasso只挑选其中一个，并将其他缩减为零。

class sklearn.linear_model.Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')

7).弹性网回归 ElasticNet Regression

ElasticNet是Lasso和Ridge回归技术的混合模型。它是用L1和L2作为正则化训练的。当有多个相关的特征时，Elastic-net是有用的，Lasso可能随机选择其中一个，Elastic-net很可能选择两个。

在Lasso和Ridge之间折衷的实际优点是它允许Elastic-Net继承一些Ridge的稳定性。

要点
* 它鼓励在高度相关变量之间的群效应；
* 对所选变量的数量没有限制；
* 它可能遭受双倍收缩率。

class sklearn.linear_model.ElasticNet(alpha=1.0, l1_ratio=0.5, fit_intercept=True, normalize=False, precompute=False, max_iter=1000, copy_X=True, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')¶

三、如何正确的选择回归模型？

在多种类型的回归模型中，重要的是基于独立和因变量的类型、数据的维度和数据的一些其他基本特征来选择最适合的技术。以下是选择正确回归模型的关键因素：

数据探索是建立预测模型的必要组成部分。它应该是你选择正确的模型之前的第一步，如识别变量的关系和影响；
为了比较不同模型的拟合程度，我们可以分析不同的指标，如参数的重要性统计、R平方、调整r平方、AIC、BIC和误差项。另一个是Mallow的Cp标准。这本质上是通过将模型与所有可能的子模型（或仔细选择它们）进行比较来检查模型中的可能偏差；
交叉验证是评估用于预测的模型的最佳方式。这里您将数据集分为两组（训练集和验证集）。观测值和预测值之间的简单均方差给出一个预测精度的指标；
如果您的数据集有多个混杂变量，您不应选择用自动模型选择的方法，因为您不想同时将它们放在一个模型中；
这也将取决于你的目标。与高度统计学显着的模型相比，一个相对不强大的模型更容易实现；
回归正则化方法（Lasso，Ridge和ElasticNet）在具有高维度和多重共线性的数据集变量上效果更好。