机器学习-线性回归理论推导-最小二乘法理论推导

其他 2019-03-22 13:50:53 阅读次数: 0

机器学习-线性回归理论推导-最小二乘法理论推导

0.概述

在统计学中，线性回归（Linear regression）是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。 ——维基百科
从最简单的只有一个自变量的简答回归来看：
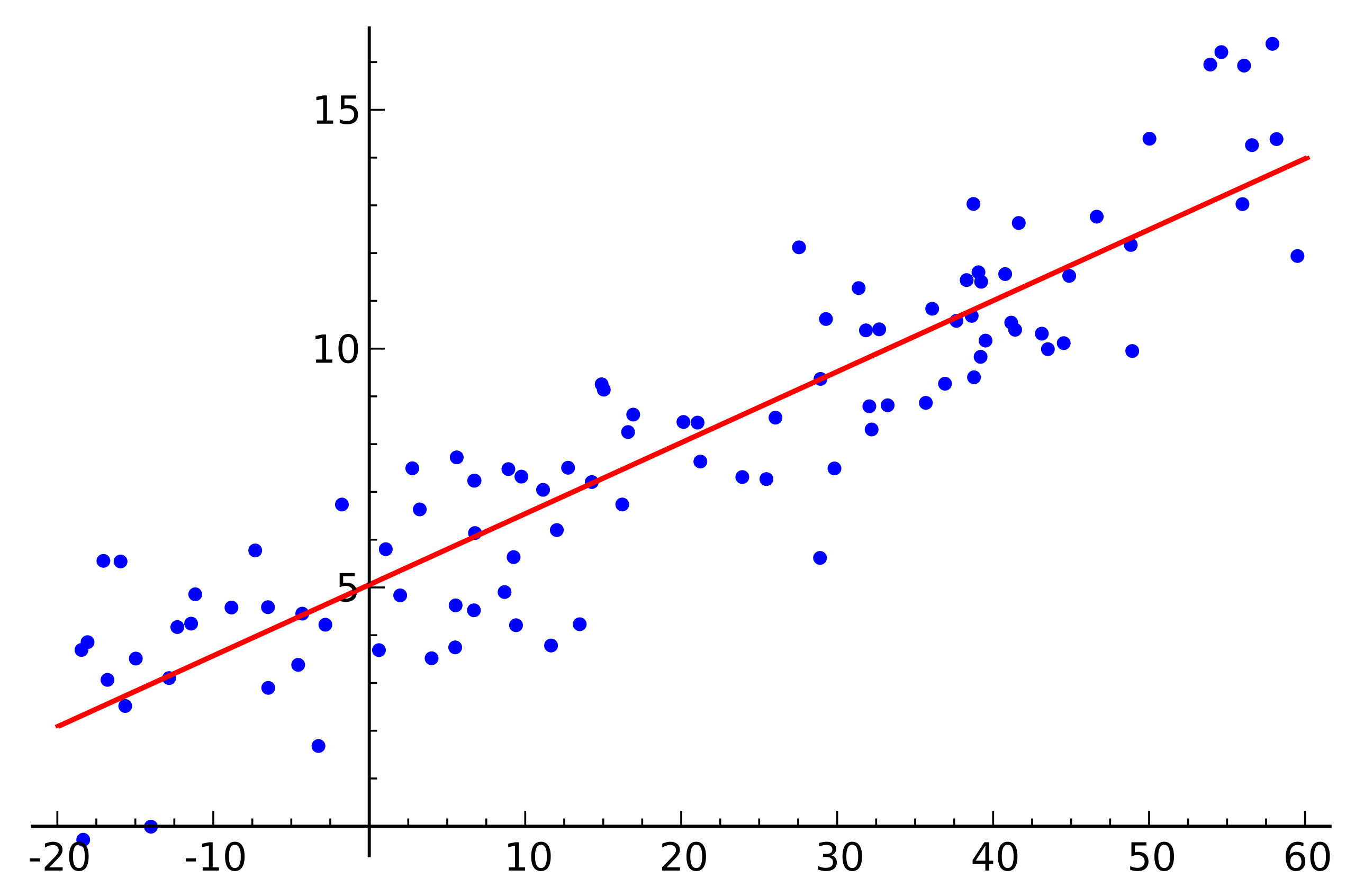
线性回归示意图
蓝点为实际样本，红线为线性预测函数，对于任意给定新的样本自变量即可按照线性预测函数进行因变量 y y 的预测。直观理想情况下，样本"应该是"均匀分布在预测函数两侧，红色预测函数从蓝色样本"居中"位置穿过去。
下面进行从理论实现对上述"直观感觉"的推导

1.线性回归理论推导

  1. 预备定理
    1. 中心极限定理
      设随机变量 X 1 , X 2 , … , X n X_1,X_2,\dots,X_n 互相独立，服从同一分布，并且具有相同的期望 μ \mu 和方差 σ 2 \sigma^2 ,则随机变量
      Y n = ∑ i = 1 n X i − n μ n σ Y_n=\frac{\sum_{i=1}^nX_i - n\mu}{\sqrt{n}\sigma}
      的分布收敛到标准正态分布，即高斯分布。
      转化一下，即可得到 ∑ i = 1 n X i \sum_{i=1}^nX_i 收敛到正态分布 N ( n μ , n σ 2 ) N(n\mu, n\sigma^2)
      简言之，当样本量足够大时，样本均值的分布慢慢变成正态分布
    2. 极大似然估计
      设总体分布为 f ( x , θ ) f(x,\theta) ， X 1 , X 2 , … , X n X_1,X_2,\dots,X_n 为该总体采样得到的样本。因为 X 1 , X 2 , … , X n X_1,X_2,\dots,X_n 独立同分布，因此，对于联合密度函数
      L ( X 1 , X 2 , … , X n ; θ 1 , θ 2 , … , θ k ) = ∏ i = 1 n f ( X i ; θ 1 , θ 2 , … , θ k ) L(X_1, X_2, \dots, X_n; \theta_1, \theta_2, \dots, \theta_k)=\prod_{i=1}^{n}f(X_i; \theta_1, \theta_2, \dots, \theta_k)
      上式中， θ \theta 被看作固定但待求解的参数；反过来，因为样本已经存在，可以看成 X 1 , X 2 , … , X n X_1,X_2,\dots,X_n 是固定的， L ( x , θ ) L(x, \theta) 是关于 θ \theta 的函数，即似然函数。
      求 θ \theta 的值，使得似然函数取极大值，这种方法就是极大似然估计
  2. 线性回归数学定义
    对于 n n 维空间(或者可以通俗的描述为 n n 维特征)的 m m 个样本，每个样本对应一个因变量 y y ，即有 m m 个样本数据如下
    ( x 1 1 , x 2 1 , … , x n 1 , y 1 ) , ( x 1 2 , x 2 2 , … , x n 2 , y 2 ) , … , ( x 1 m , x 2 m , … , x n m , y m ) (x_{1}^{1},x_{2}^{1},\dots,x_{n}^{1},y^{1}),(x_{1}^{2},x_{2}^{2},\dots,x_{n}^{2},y^{2}),\dots,(x_{1}^{m},x_{2}^{m},\dots,x_{n}^{m},y^{m})
    在上面样本的基础之上，任意给定一个新样本 ( x 1 x , x 2 x , … , x n x ) (x_{1}^{x},x_{2}^{x},\dots,x_{n}^{x}) ，如何求得该样本对应的 y x y^x 呢？如果 y y 是连续的，这就是一个回归问题，如果 y y 是离散的，就是一个分类问题，本文暂讨论回归情况。
    (对于本文初自变量只有一维的情况，线性回归目的是求得一条直线( y = a x + b y=ax+b )的方程，需要确定的量有斜率( a a )和截距( b b )两个。同理对于n维度自变量的情况，线性回归需要求得的是直线的推广——超平面的方程。此时待确定的依然是斜率和截距两个变量，但此时斜率维数变为 n n 维)
    对于上述 m m 个样本，给出线性回归的模型如下
    h θ ( x 1 , x 2 , … , x n ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta(x_{1},x_{2},\dots,x_{n})=\theta_0+\theta_{1}x_{1}+\theta_{2}x_{2}+\dots+\theta_{n}x_{n}
    其中， θ 0 \theta_0 为截距， θ i ( i = 1 , 2 , … , n ) \theta_i(i=1,2,\dots,n) 唯一确定"斜率"(注：超平面使用更多的是法向量，与"斜率"是垂直关系)。为了更加表述更加简洁，我们在截距项上增加一个 x 0 x_0 ，并且令 x 0 = 1 x_0=1 ，上述线性回归模型可以全等写成
    h θ ( x 1 , x 2 , … , x n ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta(x_{1},x_{2},\dots,x_{n})=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\dots+\theta_{n}x_{n}
    即
    h θ ( x 1 , x 2 , … , x n ) = ∑ i = 1 n θ i x i h_\theta(x_{1},x_{2},\dots,x_{n})=\sum_{i=1}^{n}\theta_{i}x_{i}
    进一步，采用矩阵表示
    h θ ( X ⃗ ) = θ ⃗ T X ⃗ h_{\theta}(\vec X)=\vec\theta^\mathrm{T} \vec X
    其中， X ⃗ \vec X 为 m × n m\times n 维矩阵， m m 为样本个数， n n 为样本维数(同特征数)， θ ⃗ T \vec\theta^\mathrm{T} 为 n × 1 n\times 1 维向量， h θ ( X ⃗ ) h_{\theta}(\vec X) 为 m × 1 m\times 1 维因变量。
  3. 线性回归推导-误差分布
    对于上述已经给定的样本点
    ( x 1 1 , x 2 1 , … , x n 1 , y 1 ) , ( x 1 2 , x 2 2 , … , x n 2 , y 2 ) , … , ( x 1 m , x 2 m , … , x n m , y m ) (x_{1}^{1},x_{2}^{1},\dots,x_{n}^{1},y^{1}),(x_{1}^{2},x_{2}^{2},\dots,x_{n}^{2},y^{2}),\dots,(x_{1}^{m},x_{2}^{m},\dots,x_{n}^{m},y^{m})
    它们是在所求线性回归 h θ ( X ⃗ ) = θ ⃗ T X ⃗ h_{\theta}(\vec X)=\vec\theta^\mathrm{T} \vec X 的"附近"，并不一定在所求的线性回归超平面上。因此，我们将已有的 m m 个样本点代入线性回归方程中时，会产生一个上下浮动的误差(扰动)，记为 ε \varepsilon 。将所有样本点代入回归方程，得到
    Y ⃗ = θ ⃗ T X ⃗ + ε ⃗ \vec Y=\vec\theta^\mathrm{T} \vec X+\vec \varepsilon
    其中， ε ⃗ \vec \varepsilon 是 m × 1 m \times 1 维向量，分别代表 m m 个样本相对于线性回归方程的上下浮动程度(误差)。
    敲黑板！ 上式中的误差 ε ⃗ \vec \varepsilon 是独立同分布的，由中心极限定理，误差分布服从均值为0，方差为某定值的正态分布，记方差为 σ 2 \sigma^2 。
  4. 线性回归推导-最大似然与最小二乘
    对于上面方程
    Y ⃗ = θ ⃗ T X ⃗ + ε ⃗ \vec Y=\vec\theta^\mathrm{T} \vec X+\vec \varepsilon
    即
    ε ⃗ = Y ⃗ − θ ⃗ T X ⃗ \vec \varepsilon=\vec Y-\vec\theta^\mathrm{T} \vec X
    对每个样本分开，有
    ε j = y j − θ ⃗ T x ⃗ j \varepsilon_j=y_j-\vec\theta^\mathrm{T} \vec x_j
    其中 j ∈ ( 1 , 2 , … , m ) j\in(1,2,\dots,m) ， x ⃗ j \vec x_j 为 1 × n 1\times n 维向量(第 j j 个样本自变量取值)， y j y_j 为第 j j 个样本因变量取值， ε j \varepsilon_j 为第 j j 个样本的误差， θ ⃗ \vec \theta 为 n × 1 n\times 1 维向量。
    由上面中心极限定理，误差分布服从均值为0，方差为 σ 2 \sigma^2 的正态分布，按照整体分布的概率密度函数进行展开
    即
    p ( ε j ) = 1 2 π σ exp ⁡ ( − ε j 2 2 σ 2 ) p(\varepsilon_j)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{{\varepsilon_j}^2}{2\sigma^2})
    将 ε j = y j − θ ⃗ T x ⃗ j \varepsilon_j=y_j-\vec\theta^\mathrm{T} \vec x_j 代入右式，得到一个关于 θ \theta 的函数
    p ( y j ∣ x j ; θ ) = 1 2 π σ exp ⁡ ( − ( y j − θ ⃗ T x ⃗ j ) 2 2 σ 2 ) p(y_j|x_j;\theta)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2}{2\sigma^2})
    再将所有样本代入，极大似然函数为 L ( θ ) = ∏ j = 1 m p ( y j ∣ x j ; θ ) L(\theta)=\prod_{j=1}^{m}p(y_j|x_j;\theta)
    L ( θ ) = ∏ j = 1 m 1 2 π σ exp ⁡ ( − ( y j − θ ⃗ T x ⃗ j ) 2 2 σ 2 ) L(\theta)=\prod_{j=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2}{2\sigma^2})
    两边取对数，令 l ( θ ) = log ⁡ L ( θ ) l(\theta)=\log L(\theta)
    l ( θ ) = log ⁡ ∏ j = 1 m 1 2 π σ exp ⁡ ( − ( y j − θ ⃗ T x ⃗ j ) 2 2 σ 2 ) l(\theta)=\log \prod_{j=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2}{2\sigma^2})
    乘积的对数等于对数的和
    l ( θ ) = ∑ j = 1 m log ⁡ 1 2 π σ exp ⁡ ( − ( y j − θ ⃗ T x ⃗ j ) 2 2 σ 2 ) l(\theta)=\sum_{j=1}^{m}\log\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2}{2\sigma^2})
    在利用一次乘积的对数等于对数的和
    l ( θ ) = m log ⁡ 1 2 π σ − 1 σ 2 ⋅ 1 2 ∑ j = 1 m ( y j − θ ⃗ T x ⃗ j ) 2 l(\theta)=m\log\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\cdot\frac{1}{2}\sum_{j=1}^{m}{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2
    可以看出等式右边第一项为常数，第二项前面的系数 1 σ 2 \frac{1}{\sigma^2} 也为常数，对求极值点无影响。求 l ( θ ) l(\theta) 极大似然估计点，即求 − 1 2 ∑ j = 1 m ( y j − θ ⃗ T x ⃗ j ) 2 -\frac{1}{2}\sum_{j=1}^{m}{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2 的极大值点，去掉负号，即求 1 2 ∑ j = 1 m ( y j − θ ⃗ T x ⃗ j ) 2 \frac{1}{2}\sum_{j=1}^{m}{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2 的极小值点，令
    J ( θ ) = 1 2 ∑ j = 1 m ( y j − θ ⃗ T x ⃗ j ) 2 J(\theta)=\frac{1}{2}\sum_{j=1}^{m}{(y_j-\vec\theta^\mathrm{T} \vec x_j)}^2
    将 h θ ( x j ) = θ ⃗ T x ⃗ j h_\theta(x_j)=\vec\theta^\mathrm{T} \vec x_j 代入
    J ( θ ) = 1 2 ∑ j = 1 m ( y j − h θ ( x j ) ) 2 J(\theta)=\frac{1}{2}\sum_{j=1}^{m}{(y_j-h_\theta(x_j))}^2
    上式第一项 y j y_j 为样本实际函数值，第二项 h θ ( x j ) h_\theta(x_j) 为线性回归预测值，现在目的就是求这两个值的差的平方最小值。这就是最小二乘法的由来，原理很简单
    目 标 函 数 = ∑ ( 样 本 值 − 预 测 函 数 值 ) 2 目标函数=\sum(样本值-预测函数值)^2
    其中，样本值就是实际观测样本的函数值，预测函数值就是线性回归函数值，目标函数就是机器学习中的损失函数。我们的求解目的就是求得使目标函数最小的线性回归函数值，也就完成了线性回归中 θ ⃗ \vec \theta 的求解。

2.最小二乘法推导

将式
J ( θ ) = 1 2 ∑ j = 1 m ( y j − h θ ( x j ) ) 2 J(\theta)=\frac{1}{2}\sum_{j=1}^{m}{(y_j-h_\theta(x_j))}^2
改为矩阵表示
J ( θ ) = 1 2 ( X ⃗ θ ⃗ − Y ⃗ ) T ( X ⃗ θ ⃗ − Y ⃗ ) J(\theta)=\frac{1}{2}(\vec X\vec\theta-\vec Y)^\mathrm{T}(\vec X\vec\theta-\vec Y)
将转置放到括号里面
J ( θ ) = 1 2 ( θ ⃗ T X ⃗ T − Y ⃗ T ) ( X ⃗ θ ⃗ − Y ⃗ ) J(\theta)=\frac{1}{2}(\vec\theta^\mathrm{T}\vec X^\mathrm{T}-\vec Y^\mathrm{T})(\vec X\vec\theta-\vec Y)
相乘展开
J ( θ ) = 1 2 ( θ ⃗ T X ⃗ T X ⃗ θ ⃗ − θ ⃗ T X ⃗ T Y ⃗ − Y ⃗ T X ⃗ θ ⃗ + Y ⃗ T Y ⃗ ) J(\theta)=\frac{1}{2}(\vec\theta^\mathrm{T}\vec X^\mathrm{T}\vec X\vec\theta-\vec\theta^\mathrm{T}\vec X^\mathrm{T}\vec Y-\vec Y^\mathrm{T}\vec X\vec\theta+\vec Y^\mathrm{T}\vec Y)
求梯度
∇ ( J ( θ ) ) = ∇ ( 1 2 ( θ ⃗ T X ⃗ T X ⃗ θ ⃗ − θ ⃗ T X ⃗ T Y ⃗ − Y ⃗ T X ⃗ θ ⃗ + Y ⃗ T Y ⃗ ) ) \nabla(J(\theta))=\nabla(\frac{1}{2}(\vec\theta^\mathrm{T}\vec X^\mathrm{T}\vec X\vec\theta-\vec\theta^\mathrm{T}\vec X^\mathrm{T}\vec Y-\vec Y^\mathrm{T}\vec X\vec\theta+\vec Y^\mathrm{T}\vec Y))
∇ ( J ( θ ) ) = 1 2 ( 2 X ⃗ T X ⃗ θ ⃗ − X ⃗ T Y ⃗ − ( Y ⃗ T X ⃗ ) T ) \nabla(J(\theta))=\frac{1}{2}(2\vec X^\mathrm{T}\vec X\vec\theta-\vec X^\mathrm{T}\vec Y-(\vec Y^\mathrm{T}\vec X)^\mathrm{T})
最后一项转置写开
∇ ( J ( θ ) ) = 1 2 ( 2 X ⃗ T X ⃗ θ ⃗ − X ⃗ T Y ⃗ − X ⃗ T Y ⃗ ) \nabla(J(\theta))=\frac{1}{2}(2\vec X^\mathrm{T}\vec X\vec\theta-\vec X^\mathrm{T}\vec Y-\vec X^\mathrm{T}\vec Y)
合并
∇ ( J ( θ ) ) = 1 2 ( 2 X ⃗ T X ⃗ θ ⃗ − 2 X ⃗ T Y ⃗ ) \nabla(J(\theta))=\frac{1}{2}(2\vec X^\mathrm{T}\vec X\vec\theta-2\vec X^\mathrm{T}\vec Y)
∇ ( J ( θ ) ) = X ⃗ T X ⃗ θ ⃗ − X ⃗ T Y ⃗ \nabla(J(\theta))=\vec X^\mathrm{T}\vec X\vec\theta-\vec X^\mathrm{T}\vec Y
求梯度的驻点，令 ∇ ( J ( θ ) ) = 0 \nabla(J(\theta))=0 ，即
X ⃗ T X ⃗ θ ⃗ − X ⃗ T Y ⃗ = 0 \vec X^\mathrm{T}\vec X\vec\theta-\vec X^\mathrm{T}\vec Y=0
X ⃗ T X ⃗ θ ⃗ = X ⃗ T Y ⃗ \vec X^\mathrm{T}\vec X\vec\theta=\vec X^\mathrm{T}\vec Y
最终得到参数 θ \theta 的解析式
θ = ( X ⃗ T X ⃗ ) ⃗ − 1 X ⃗ T Y ⃗ \theta=(\vec X^\mathrm{T}\vec X\vec)^{-1}\vec X^\mathrm{T}\vec Y
上述推导需要用到 X ⃗ T X ⃗ \vec X^\mathrm{T}\vec X 的逆，因此要求 X ⃗ T X ⃗ \vec X^\mathrm{T}\vec X 满秩或者正定。然而现实任务中 X ⃗ T X ⃗ \vec X^\mathrm{T}\vec X 往往不是满秩的。例如有的任务会使用到大量特征，甚至特征的个数会超过样本数，此时 X ⃗ T X ⃗ \vec X^\mathrm{T}\vec X 显然不满秩。为此，引入正则项，对任意 λ > 0 \lambda>0 ， X ⃗ T X ⃗ + λ I \vec X^\mathrm{T}\vec X+\lambda I 正定， I I 为单位阵。参数解析式优化为
θ = ( X ⃗ T X ⃗ + ⃗ λ I ) − 1 X ⃗ T Y ⃗ \theta=(\vec X^\mathrm{T}\vec X\vec+\lambda I)^{-1}\vec X^\mathrm{T}\vec Y

3.为什么不使用最小二乘法

上节对最小二乘法进行了理论上的推导，得到的结果可以说是很漂亮的，但是在实际的操作中却不常使用，原因如下：

  1. X ⃗ T X ⃗ \vec X^\mathrm{T}\vec X 可能不是正定的，加入正则项可以解决；
  2. X ⃗ T X ⃗ \vec X^\mathrm{T}\vec X 在数据量很大的时候计算量特别大；
  3. 最小二乘法只适应于线性回归；
  4. 回归问题常使用的方法有梯度下降法和牛顿法以及拟牛顿法等。

4.小结

本文从最简单一维样本情况引出线性回归的概念，进而使用中心极限定理说明样本点与回归函数值之间的误差的分布是服从均值为0的正态分布。使用最大似然估计推导出最小二乘法，然后利用梯度为0求出最小二乘的驻点。最终给出线性回归参数 θ \theta 的解析式。
如有不妥，请指示正，谢谢阅读！
作者：togetlife

猜你喜欢

转载自blog.csdn.net/togetlife/article/details/88409640
今日推荐
面壁智能发布 Eurux-8x22B 开源大模型 —— 堪称「理科状元」
开源日报 | 谷歌扶持鸿蒙上位；开源Rabbit R1；Docker加持的安卓手机；微软的焦虑和野心；海尔电器把开放平台关了
中国码农的“35岁魔咒”
蘭雅 CorelDRAW 插件 2024.5.1 国际劳动节版，免费下载
Arc Browser for Windows 1.0 正式 GA
90后程序员开发视频搬运软件、不到一年获利超 700 万，结局很刑！
周排行
【转】spring中对控制反转和依赖注入的理解
tms webcore 安装和使用
java程序员进阶相关书籍
SpringMVC接受请求参数、
如何保存训练好的机器学习模型
MyEclipse、Eclipse设置项目JDK的三个地方
商超行业微信小程序开发定制一般多少钱 （行业技术人员解读）
Markdown编辑器语言——30分钟入门到到精通
Linux系统下MongoDB的简单安装与基本操作
Power Strings
每日归档
更多
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)
2024-05-03(19)
2024-05-02(0)
2024-05-01(4)
2024-04-30(1)
2024-04-29(40)
2024-04-28(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022