古典概型计算概率：钥匙乱序问题(Derangement)

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/lynn0085/article/details/83628256

在文章 古典概型事件数计算, 分房，配对，乱序 (概统1)
中学习了几种古典概型概率的计算方法，不过最后一题写得不够详细，本篇文章进行补充。

【古典概型计算概率：乱序问题(Derangement)】
【钥匙乱序】
有外形相同的n把锁和n把钥匙，每把钥匙只能打开其中的一把锁，现将锁和钥匙随机配对，每对锁和钥匙各一把，试求至少有一把锁能被所配对钥匙打开的概率。

注意，同样是配对问题，与选择手套问题不同的是，手套问题可以只选部分，本题是全选，全排序，全乱序。

至少有一把锁能配对 = 有一把锁能配对 + 有两把锁能配对 +… + 有n把锁能配对

本题如果按照古典概率去求，比较难计算，因为很多情况交集在一起，不如按照概率公式去求，
例如三个事件的情况：P(AUBUC)=P(A)+P(B)+P©-P(AB)-P(AC)-P(BC)+P(ABC)

本题，至少有一把锁能配对，可以表示成
$\bigcup_{i=1}^{n}A_{i}$

P( $\bigcup_{i=1}^{n}A_{i}$) = $\sum_{i=1}^{n}P(A_{i})$ - $\sum_{1\leqslant i< j\leqslant n}^{n}P(A_{i}A_{j})$ + $\sum_{1\leqslant i< j<k\leqslant n}^{n}P(A_{i}A_{j}A_{k})$ + … + $(-1)^{n-1}P(A_{1}A_{2}...A_{n})$

$\sum_{i=1}^{n}P(A_{i})$ = 有一把配成功 = $C_{n}^{1}$ $\frac{(n-1)!}{n!}$

其中，有一把能成功配对的概率计算是
$\ P(A_{i})$ = $\frac{(n-1)!}{n!}$，这个是怎样得到的呢？

${\color{Red}{ 首先必须要明白的是，P(A_{i}) =\frac{(n-1)!}{n!}这个事件中，}}$
${\color{Red}{ 不仅仅只是第 i 把锁独立配对成功的事件，}}$
${\color{Red}{ 它同时也包含了第 i 把锁与其他锁同时配对成功的事件，}}$
${\color{Red}{ 它代表的是凡是包含有第 i 把锁配对成功的所有事件。 }}$

${\color{Red}{ P(A_{i})包含了所有 包括第 i 把锁在内成功配对的概率。}}$

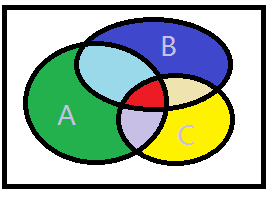
就是类似下图的样本空间的模型，假设A代表第 i 把钥匙配对成功，A的样本空间包含了与其他同时配对成功的样本。

$\sum_{i=1}^{n}P(A_{i})$ = 有一把配成功 = $C_{n}^{1}$ $\frac{(n-1)!}{n!}$

那么，假设是第 i 把配对成功，变成
$P(A_{i})$ = 有一把配成功 = $\frac{(n-1)!}{n!}$
$\frac{(n-1)!}{n!}$， 这个是怎样得出的？

举个例子，假设 有 4把锁，4把钥匙，计算第一把钥匙配对成功的概率。
下面列出所有的事件组合

锁1 — 钥1 钥1 钥1 钥1 钥1 钥1 钥2 钥2 钥2 钥2 钥2 钥2
锁2 — 钥2 钥2 钥3 钥3 钥4 钥4 钥1 钥1 钥3 钥3 钥4 钥4
锁3 — 钥3 钥4 钥2 钥4 钥2 钥3 钥3 钥4 钥2 钥4 钥2 钥3
锁4 — 钥4 钥3 钥4 钥2 钥3 钥2 钥4 钥3 钥4 钥2 钥3 钥2

锁1 — 钥3 钥3 钥3 钥3 钥3 钥3 钥4 钥4 钥4 钥4 钥4 钥4
锁2 — 钥1 钥1 钥2 钥2 钥4 钥4 钥1 钥1 钥2 钥2 钥3 钥3
锁3 — 钥3 钥4 钥1 钥4 钥1 钥2 钥2 钥3 钥1 钥3 钥1 钥2
锁4 — 钥4 钥3 钥4 钥1 钥2 钥1 钥3 钥2 钥3 钥1 钥2 钥1

由上图可以看出，4把钥匙的所有事件就是4的全排列=4！= 24。

那么第一把锁能成功配对的事件只有钥匙1排在最前面的前面那6个事件，
　　在这6个事件中，除了钥匙1以外的其他钥匙构成一个全排列，就是3！=6。
　　而且在这6个事件中，除了钥1配对成功外，还包含了1个钥1，钥2，钥3和钥4同时配对成功的1个事件。
　　除去4个同时配对成功外，还包含了有且只有钥1与钥2同时配对成功（但其他没有配对成功）1个，有且只有钥1与钥3同时配对成功有1个，有且只有钥1与钥4同时配对成功也有1个。

所以说在4把钥匙4把锁的事件中，第１把钥匙能成功配对的事件数是(4-1)！＝３！，所有事件数是4！。

$P(A_{1})$ = 第一把能配成功 = $\frac{(4-1)!}{4!}$
$P(A_{i})$ = 第 i 把能配成功 = $\frac{(4-1)!}{4!}$

推广开来，假设是n把钥匙，n把锁，
$P(A_{i})$ = 第 i 把能配成功 = $\frac{(n-1)!}{n!}$

有两把同时配对成功的总事件数还是 n!，有效事件数是 (n-2)!
概率计算是，
$P(A_{i}A_{j})$ = 有两把同时配成功 = $\frac{(n-2)!}{n!}$

所以，
$\sum_{1\leqslant i< j\leqslant n}^{n}P(A_{i}A_{j})$ = 有两把同时配成功 = $C_{n}^{2}$ $\frac{(n-2)!}{n!}$

有n把同时配成功的事件数 = $(-1)^{n-1}C_{n}^{n}*\frac{1}{n}$

最后

P( $\bigcup_{i=1}^{n}A_{i}$) = $C_{n}^{1}$ $\frac{(n-1)!}{n!}$ - $C_{n}^{2}$ $\frac{(n-2)!}{n!}$ + $C_{n}^{3}$ $\frac{(n-3)!}{n!}$ + … + $(-1)^{n-1}C_{n}^{n}*\frac{1}{n}$

= $1-\frac{1}{2!}+\frac{1}{3!} + ... +(-1)^{n-1}\frac{1}{n!}$

这个就是著名的”乱序问题“
这个问题属于著名的“乱序问题”(Derangement)。

N把锁和N把钥匙无一配对的几率是
P(N)= $\sum_{i=0}^{\infty }\frac{(-1)^{i}}{i!}$
= $\frac{1}{2!}-\frac{1}{3!} + ... +(-1)^{n}\frac{1}{n!}$= $\lim_{n->\infty}\frac{1}{e}$

至少有1把配对的概率就是1-P(N)。
当N→∞时,P(N)→( $\frac{1}{e}$)，
至少有1把配对的概率就趋于( $1-\frac{1}{e}$)

============
参考链接
古典概型事件数计算, 分房，配对，乱序 (概统1)