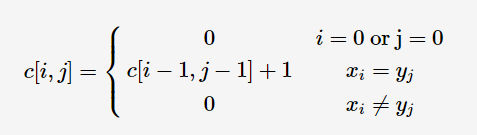学习算法（1）----动态规划（Dynamic Programming）

记一点我的心得和学习到的东西。学习了几篇博文：

https://blog.csdn.net/lz161530245/article/details/76943991 //也存在三个串的最长公共子序列代码

/* 欢迎指正与讨论 */

首先是这一句话：those who cannot remember the past are condemned to repeat it

对于动态规划我心中觉得最重要的点就是：

记录，走过的路，无论通不通，都要记录下来。

大问题化为小问题，也就是常说的，最优子结构（子结构）。

子结构设计的好，问题解决的就很舒服。走过的路一定要记录，并且继续走的时候要知道，这条路走不通，不要再走了。

硬币问题
我们有面值为1元3元5元的硬币若干枚，如何用最少的硬币凑够11元？

思路：我们最简单的知道 1元用一个1元，2元用2个1元，3元用1个3元，4元用1+3元，5元用1个5元。

那么11元或者N元，是不是可以选用1+10元、2+9元、3+8元、4+7元、5+6元中最少的呢？（1-5小于11的一半）

这样是可以的，但是这种方法，如果是11111元呢，显然略微有点多。

那么我们需要再看一下我们已有的条件，有1.3.5三种硬币，那么，所有N元，都必然是用1/3/5元组成。

那么，N=（N-1） + 1、（N-3） + 3、（N-5） + 5 。这种方法显然更舒服一些，因为 N只用 1 3 5 组成，一定是由这三种组成的。

小朋友过桥问题

在一个夜黑风高的晚上，有n（n <= 50）个小朋友在桥的这边，现在他们需要过桥，但是由于桥很窄，每次只允许不大于两人通过，他们只有一个手电筒，所以每次过桥的两个人需要把手电筒带回来，i号小朋友过桥的时间为T[i]，两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。

问题分析：首先将n个小朋友按过河时间从小到大排序，设第i个小朋友过河的时间为T[i]。假设n个小朋友过河的总时间为f(n)，

则f(1)=T[1]; f(2)=T[2];f(3)=T[2]+T[1]+T[3]。

假设有n个小朋友(n>=4)：
1,2号小朋友过河，时间为T[2]
1号小朋友回来，时间为T[1]
n-1,n号小朋友过河，时间为T[n]
2号小朋友回来，时间为T[2]
此时，河这边有1号到n-2号的所有小朋友，所以时间为f(n-2)
所以过河总时间f(n) =T[2]+T[1]+T[n]+T[2]+f(n-2)

通过以上表述我们可以得到如下递推公式：
f(1)=T[1]
f(2)=T[2]
f(3)=T[1] + T[2] + T[3]
f(n) = T[1]+2T[2]+T[n] + f(n-2); n>=4

假设有n个小朋友(n>=4)：
1号小朋友回来，时间为T[1]
1，n号小朋友过河，时间为T[n]
此时，河这边有1号到n-1号的所有小朋友，所以时间为f(n-1)
所以过河总时间f(n) =T[1]+T[n]+f(n-1)

通过以上表述我们可以得到如下递推公式：
f(1)=T[1]
f(2)=T[2]
f(3)=T[1] + T[2] + T[3]
f(n) = T[1]T[n] + f(n-1); n>=4

取两者中最小的，就是最快时间。具体代码见引用。

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
 
int main()
{
   int n;
	cin>>n;
	int *t = new int[n];
	for (int i=0;i<n;i++)
	{
		cin>>t[i];
	}
	sort(t,t+n);
	vector<int> vect(n);
	vect[0]=0;
	vect[1]=t[1];
	for (int i=2;i<n;i++)
	{
		vect[i] = min(vect[i-1]+t[0]+t[i],vect[i-2]+t[0]+t[i]+2*t[1]);
	}
	cout<<vect[n-1];
 
	return 0;
}

最长公共子序列

设串x[m],y[n] 其公共子序列是 LCS(x[0~m-1],y[0~n-1])

分析：设x={1,3,4,5,6,7,7,8},y={3,5,7,4,8,6,7,8,2}。(首先看到两个串，思考的是直接进行比较无从下手，因为存在1234 与 4321 的这种极端情况，导致一个字符比较过后不能够直接舍弃，因为还需要留存下来与所有字符比较 [从后向前看的话，4与1比较不相等，但是不能舍弃4与1因为还需要继续与剩余的其他字符比较])

既然无法一次性比较出结果，那么我们是否可以从短的串来比较？是否可以用空间来换取时间的缩短？是否可以记录足够多的数据来进行解算？ LCS(x,y)是否可以向前递推？(因为我们比较过一次之后，知道了一对字符不相等了，那么就一定要记录下来，不然就不需要算法了。)

从尾字符看起，8与2 不相等，下一步一定不是继续比较x,y的倒数第二个字符 7与8，8与2不相等只代表了这两个尾字符不匹配。

因为x的尾字符8 还要与 y的倒数第二个字符8比较。同样y的尾字符2还要与x的倒数第二个字符7比较。并且会一直比到y[0]。

但是到这里我们已经比较过8与2了，那么我们就一定要记录下来，比较过的，走过的路一定要记录下来。

那么LCS(x,y)与LCS(x-1,y-1),LCS(x-1,y),LCS(x,y-1).会不会有关系呢？关系如下图：

x与y的尾字符，8与2不相等。代表了串x与串y的LCS计算中，需要比较 串x-1与串y，串x与串y-1，两者中取长的。

也就是所谓的记录下来x与y的尾字符不相等，所以不需要再次比较两者，但是两者仍需要与其他字符比较。

若x与y的尾字符相等，那么LCS(x,y)就等于LCS(x-1,y-1)+1。因为既然尾字符相等，那么尾字符相互对应就好了不需要再次计算了，可以从两个串中一起拆除。分布的实现方法见开篇的转载链接或者自己手动推导一下。

最长公共子串，类似于最长公共子序列。转移方程：

学习算法（1）----动态规划（Dynamic Programming）

猜你喜欢