一、 自我理解
Those who cannot remember the past are condemned to repeat it.
这里的Programming不是"编程",“规划”的意思,而是“表方法”。就是计算机中有一个存储数据的集合(缓存)将计算过的东西放在缓存里,下次再做类似的计算的时候,在缓存里去看看这个结果自己是否计算过,如果计算过,则直接将这个结果拿出来用。(缓存已经计算过的东西,将中间值存起来,这也是动态规划的核心)
下面是关于动态规划的英文解释:
dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.
也就是说,动态规划一定是具备了以下三个特点:
- 把原来的问题分解成了几个相似的子问题。(强调“相似子问题”)
- 所有的子问题都只需要解决一次。(强调“只解决一次”)
- 储存子问题的解。(强调“储存”)
————————————————————————————————————————————————————————
什么是动态规划?
1、引入一个幼儿园问题
A:"1+1+1+1+1=?"
A:"上面等式的值是多少?"
B:计算:5
A:“那么上面的等式的值加上“1+”等于多少呢?”
B:6
A:"你怎么算的这么快?"
B:"只要在5的基础上加上1就行了啊。"
上面的对话看似简单却告诉了一个思想:记住求过的解来节省时间。
2、我们来看看最经典的——斐波那契数列(Fibonacci)的例子!
1, 1, 2, 3, 5, 8, 13 ,21 ...
如果我们把第n个斐波拉契数记作 Fibonacci(n),那么怎样利用动态规划来计算这个数呢?
根据动态规划的三个特点,首先,我们需要把原问题分解成几个相似的子问题。这里还蛮清晰的啦,子问题就是这两个:Fibonacci(n-1) 和 Fibonacci(n-2)。
而原问题和子问题之间的关系是:
(其中Fibonacci(0)=Fibonacci(1)=1)
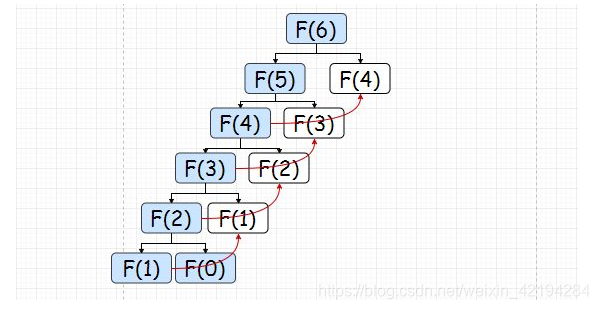
假设我们现在需要计算n=6的时候,斐波拉契的值,那么我们就需要计算他的子问题Fibonacci(5)和Fibonacci(4)。同理对于Fibonacci(5)我们需要计算Fibonacci(4)和Fibonacci(3),对于Fibonacci(4)我们需要计算Fibonacci(3)和Fibonacci(2)。这样的话,最后我们需要计算的东西如下图——由最顶向下不停的分解问题,最后往上返回结果。
显然,这是一个非常低效的方法,因为其中有大量的重复计算。并且不满足动态规划的第二个特点:“所有的子问题都只需要解决一次“。
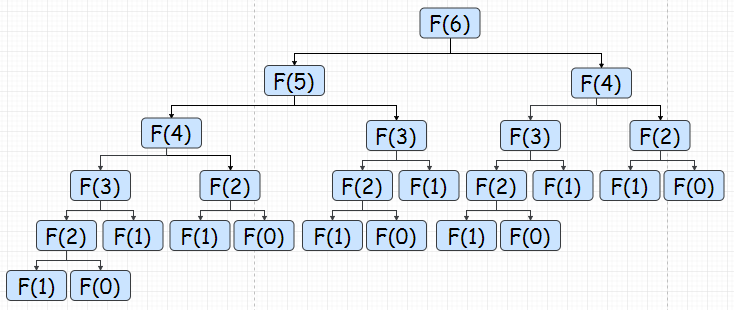
这个问题很好解决,我们只需要利用动态规划的第三个特点——”储存子问题的解“就可以了。比如,如果已经计算过Fibonacci(3),那么把结果储存起来,其他地方碰到需要求Fibonacci(3)的时候,就不需要计算,直接调用结果就行。这样做之后,蓝色表示需要进行计算的,白色表示可以直接从存储中取得结果的:
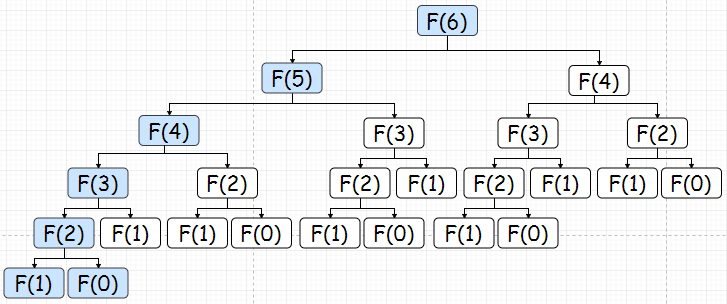
也就是如下的计算(红色箭头表示调用了储存的数据,并未进行计算):
-
也就是如下的计算(红色箭头表示调用了储存的数据,并未进行计算):
所以动态规划的核心思想就是:记住已经求过的解来节省时间。
-
动态规划算法的两种形式:1、自顶向下的备忘录法 2、自顶向上(时间复杂度和空间复杂度都是最低的)
-
package practice;
public class Fibonacci {
/**自顶向下的思考方式(递归)、动态规划(备忘录法)
*/
// public static int f(int n) {
// if(n==0) {
// return 0;
// }
// if (n==1){
// return 1;
//
// }
// return f(n-1)+f(n-2);
// }
// public static int f(int n,int []bak ) {
// if(n==0) {
// return 0;
// }
// if (n==1){
// return 1;
//
// }
// if (bak[n]!=-1) {
// return bak[n];
// }
// int result =f(n-1,bak)+f(n-2,bak);
// bak[n]=result;
// return result;
// }
/**自底向上的方法
*/
public static int f(int n) {
if(n==0) {
return 0;
}
if (n==1){
return 1;
}
int r1=0;
int r2=1;
int result =0;
for(int i=2;i<=n;i++) {
result=r1+r2;
r1=r2;
r2=result;
}
return result;
}
/**
* 自底向上
* @param args
*/
public static void main(String[] args){
int n=5;
System.out.println(f(5));
}
}二、动态规划性质浅谈
首先,动态规划和递推有些相似(尤其是线性动规),但是不同于递推的是:
递推求出的是数据,所以只是针对数据进行操作;而动态规划求出的是最优状态,所以必然也是针对状态的操作,而状态自然可以出现在最优解中,也可以不出现——这便是决策的特性(布尔性)。
其次,由于每个状态均可以由之前的状态演变形成,所以动态规划有可推导性,但同时,动态规划也有无后效性,即每个当前状态会且仅会决策出下一状态,而不直接对未来的所有状态负责,可以浅显的理解为——
Future never to do with past time,but present does.
现在决定未来,未来与过去无关。
三、扯正题——子序列问题
(一)一个序列中的最长上升子序列( LISLIS )
例:由6个数,分别是: 1 7 6 2 3 4,求最长上升子序列。
评析:首先,我们要理解什么叫做最长上升子序列:1、最长上升子序列的元素不一定相邻 2、最长上升子序列一定是原序列的子集。所以这个例子中的 LISLIS 就是:1 2 3 4,共4个
1、 n^2n2 做法
首先我们要知道,对于每一个元素来说,最长上升子序列就是其本身。那我们便可以维护一个 dpdp 数组,使得 dp[i]dp[i]表示以第 ii 元素为结尾的最长上升子序列长度,那么对于每一个 dp[i]dp[i] 而言,初始值即为 11 ;
那么dp数组怎么求呢?我们可以对于每一个 ii ,枚举在 ii 之前的每一个元素 jj ,然后对于每一个 dp[j]dp[j] ,如果元素 ii大于元素 jj ,那么就可以考虑继承,而最优解的得出则是依靠对于每一个继承而来的 dpdp 值,取 maxmax .
for(int i=1;i<=n;i++) { dp[i]=1;//初始化 for(int j=1;j<i;j++)//枚举i之前的每一个j if(data[j]<data[i] && dp[i]<dp[j]+1) //用if判断是否可以拼凑成上升子序列, //并且判断当前状态是否优于之前枚举 //过的所有状态,如果是,则↓ dp[i]=dp[j]+1;//更新最优状态 }最后,因为我们对于 dpdp 数组的定义是到i为止的最长上升子序列长度,所以我们最后对于整个序列,只需要输出 dp[n]dp[n] ( nn 为元素个数)即可。
从这个题我们也不难看出,状态转移方程可以如此定义:
下一状态最优值=最优比较函数(已经记录的最优值,可以由先前状态得出的最优值)
——即动态规划具有 判断性继承思想
2、 nlognnlogn 做法
我们其实不难看出,对于 n^2n2 做法而言,其实就是暴力枚举:将每个状态都分别比较一遍。但其实有些没有必要的状态的枚举,导致浪费许多时间,当元素个数到了 10^4-10^5104−105 以上时,就已经超时了。而此时,我们可以通过另一种动态规划的方式来降低时间复杂度:
将原来的dp数组的存储由数值换成该序列中,上升子序列长度为i的上升子序列,的最小末尾数值
这其实就是一种几近贪心的思想:我们当前的上升子序列长度如果已经确定,那么如果这种长度的子序列的结尾元素越小,后面的元素就可以更方便地加入到这条我们臆测的、可作为结果、的上升子序列中。
qwq一定要好好看注释啊!
int n; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; f[i]=0x7fffffff; //初始值要设为INF /*原因很简单,每遇到一个新的元素时,就跟已经记录的f数组当前所记录的最长 上升子序列的末尾元素相比较:如果小于此元素,那么就不断向前找,直到找到 一个刚好比它大的元素,替换;反之如果大于,么填到末尾元素的下一个q,INF 就是为了方便向后替换啊!*/ } f[1]=a[1]; int len=1;//通过记录f数组的有效位数,求得个数 /*因为上文中所提到我们有可能要不断向前寻找, 所以可以采用二分查找的策略,这便是将时间复杂 度降成nlogn级别的关键因素。*/ for(int i=2;i<=n;i++) { int l=0,r=len,mid; if(a[i]>f[len])f[++len]=a[i]; //如果刚好大于末尾,暂时向后顺次填充 else { while(l<r) { mid=(l+r)/2; if(f[mid]>a[i])r=mid; //如果仍然小于之前所记录的最小末尾,那么不断 //向前寻找(因为是最长上升子序列,所以f数组必 //然满足单调) else l=mid+1; } f[l]=min(a[i],f[l]);//更新最小末尾 } } cout<<len;Another \ \ SituationAnother Situation
但是事实上, nlognnlogn 做法偷了个懒,没有记录以每一个元素结尾的最长上升子序列长度。那么我们对于 n^2n2 的统计方案数,有很好想的如下代码(再对第一次的 dpdp 数组 dpdp 一次):
for(i = 1; i <= N; i ++){ if(dp[i] == 1) f[i] = 1 ; for(j = 1; j <= N: j ++) if(base[i] > base[j] && dp[j] == dp[i] - 1) f[i] += f[j] ; else if(base[i] == base[j] && dp[j] == dp[i]) f[i] = 0 ; if(f[i] == ans) res ++ ; }但是 nlognnlogn 呢?虽然好像也可以做,但是想的话会比较麻烦,在这里就暂时不讨论了 qwqqwq ,但笔者说这件事的目的是为了再次论证一个观点:时间复杂度越高的算法越全能
33 、输出路径
只要记录前驱,然后递归输出即可(也可以用栈的)
下面贴出 n ^ 2n2 的完整代码qwq
#include <iostream> using namespace std; const int MAXN = 1000 + 10; int n, data[MAXN]; int dp[MAXN]; int from[MAXN]; void output(int x) { if(!x)return; output(from[x]); cout<<data[x]<<" "; //迭代输出 } int main() { cin>>n; for(int i=1;i<=n;i++)cin>>data[i]; // DP for(int i=1;i<=n;i++) { dp[i]=1; from[i]=0; for(int j=1;j<i;j++) if(data[j]<data[i] && dp[i]<dp[j]+1) { dp[i]=dp[j]+1; from[i]=j;//逐个记录前驱 } } int ans=dp[1], pos=1; for(int i=1;i<=n;i++) if(ans<dp[i]) { ans=dp[i]; pos=i;//由于需要递归输出 //所以要记录最长上升子序列的最后一 //个元素,来不断回溯出路径来 } cout<<ans<<endl; output(pos); return 0; }(二)两个序列中的最长公共子序列( LCSLCS )
1、譬如给定2个序列:
1 2 3 4 5 3 2 1 4 5试求出最长的公共子序列。
qwqqwq 显然长度是 33 ,包含 3 \ \ 4 \ \ 53 4 5 三个元素(不唯一)
解析:我们可以用 dp[i][j]dp[i][j] 来表示第一个串的前 ii 位,第二个串的前j位的 LCSLCS 的长度,那么我们是很容易想到状态转移方程的:
如果当前的 A1[i]A1[i] 和 A2[j]A2[j] 相同(即是有新的公共元素) 那么
dp[ i ] [ j ] = max(dp[ i ] [ j ], dp[ i-1 ] [ j-1 ] + 1);dp[i][j]=max(dp[i][j],dp[i−1][j−1]+1);
如果不相同,即无法更新公共元素,考虑继承:
dp[ i ] [ j ] = max(dp[ i-1 ][ j ] , dp[ i ][ j-1 ]dp[i][j]=max(dp[i−1][j],dp[i][j−1]
那么代码:
#include<iostream> using namespace std; int dp[1001][1001],a1[2001],a2[2001],n,m; int main() { //dp[i][j]表示两个串从头开始,直到第一个串的第i位 //和第二个串的第j位最多有多少个公共子元素 cin>>n>>m; for(int i=1;i<=n;i++)scanf("%d",&a1[i]); for(int i=1;i<=m;i++)scanf("%d",&a2[i]); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { dp[i][j]=max(dp[i-1][j],dp[i][j-1]); if(a1[i]==a2[j]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1); //因为更新,所以++; } cout<<dp[n][m]; }22 、而对于洛谷 P1439P1439 而言,不仅是卡上面的朴素算法,也考察到了全排列的性质:
对于这个题而言,朴素算法是 n^2n2 的,会被 10^5105 卡死,所以我们可以考虑 nlognnlogn 的做法:
因为两个序列都是 1~n1 n 的全排列,那么两个序列元素互异且相同,也就是说只是位置不同罢了,那么我们通过一个 mapmap 数组将 AA 序列的数字在 BB 序列中的位置表示出来——
因为最长公共子序列是按位向后比对的,所以a序列每个元素在b序列中的位置如果递增,就说明b中的这个数在a中的这个数整体位置偏后,可以考虑纳入 LCSLCS ——那么就可以转变成 nlognnlogn 求用来记录新的位置的map数组中的 LISLIS 。
最后贴 ACAC 代码:
#include<iostream> #include<cstdio> using namespace std; int a[100001],b[100001],map[100001],f[100001]; int main() { int n; cin>>n; for(int i=1;i<=n;i++){scanf("%d",&a[i]);map[a[i]]=i;} for(int i=1;i<=n;i++){scanf("%d",&b[i]);f[i]=0x7fffffff;} int len=0; f[0]=0; for(int i=1;i<=n;i++) { int l=0,r=len,mid; if(map[b[i]]>f[len])f[++len]=map[b[i]]; else { while(l<r) { mid=(l+r)/2; if(f[mid]>map[b[i]])r=mid; else l=mid+1; } f[l]=min(map[b[i]],f[l]); } } cout<<len; return 0 }