目录
递归与动态规划之间的联系（Recursion and Dynamic Programming）：
引言：
动态规划是算法中的一个重点，我第一次碰见它是在大二下学期的学位课 ——《算法设计与分析》，无奈当时只是为了应付学校的期末考试学的非常浅，最近在B站上看到了关于动态规划算法的视频，并再次对动态规划进行学习，所以写这篇文章来对动态规划算法的重新学习进行一个记录。
分析：
递归（Recursion）：
为什么在这里要提到递归？其实递归算法和动态规划算法之间是有联系的，我们在后面分析递归实现斐波那契数列时会明确这一点。
在我之前的这篇文章C语言-8月1日-递归与动态内存管理中曾经写过关于递归的知识，在这里对递归的定义再提一遍：
程序调用自身的编程技巧称之为递归（Recursion）
递归个人认为也是一个极具数学思维的编程技巧，因为在递归的过程中包含了把一个复杂问题分解为多个规模较小的问题，还有分解完成之后将等规模的问题合并为原问题规模的过程。在之前的文章里我曾经使用递归技巧实现了斐波那契数列、杨辉三角、约瑟夫环等数学问题，在实现杨辉三角的三种主流方法（一维数组、二维数组、递归）里递归也是占用内存最小且效率最高的那一个。好了，废话不多说，我们来分析斐波那契数列。
递归斐波那契数列（Fibonnaci Sequence）：
斐波那契数列在之前的文章中已经使用递归技巧实现过并分析过函数调用的过程，这里给出代码和树状图：
斐波那契数列的递归函数：
int Fibonnaci(int n)
{
if(n == 1 || n == 2){//递归出口
return 1;
}
else{
return Fibonnaci(n - 1) + Fibonnaci(n - 2);//递归核心语句，除了第一个和第二个值任何一个值都等于它前面两个值相加的总和
}
}斐波那契数列递归形式的分析树状图：
在这张图中我们可以看到我们要求的是斐波那契数列中的第六个数字，我们将要求的第六个数字的个问题分解为要求第五个数字和第四个数字，然后又分别将求第五个数字和求第四个数字分解为求第四个数字和第三个数字与求第三个数字和第二个数字，第二个数字和第一个数字其实也就是递归出口1，所以此时第三个数字为2，第四个数字就为3，第五个数字就为5，第六个数字就为8，数字8就是最终的结果。
但是在这张树状图里，我们却进行了一个极度消耗内存空间的行为——函数调用。
如图，例如我们在已经通过第三层的左子树Fibo(4)下面的子树求出Fibo（4）的前提下，还要通过第二层右子树下面的调用进行再一次的求值，也就是说要求的值每增长一个树的规模就会放大一倍，所以基于这种方式下的递归斐波那契数列这个程序的时间复杂度就是恐怖的O(2^n).
递归与动态规划之间的联系（Recursion and Dynamic Programming）：
上面我们已经分析了常规状态下递归形式的斐波那契数列的求解方式，但是由于这种方式的时间复杂度过大，我们由此引入一个新的知识点：重叠子问题（Overlap sub-problem）
重叠子问题（Overlap sub-problem）
在斐波那契数列求解的树状图中，我们要进行多次并重复的函数调用，且调用的次数是呈指数级增长的，但是如果我们把每一次算出来的值保存起来在后面直接进行调用，例如我们需要继续按斐波那契数列的第六个树，在第四个数和第五个树已经算出来的前提下，我们直接拿出来用，复杂程度就会简单不少，且能加速整个运算过程的速度这里画一张图我们来看一下这个过程：
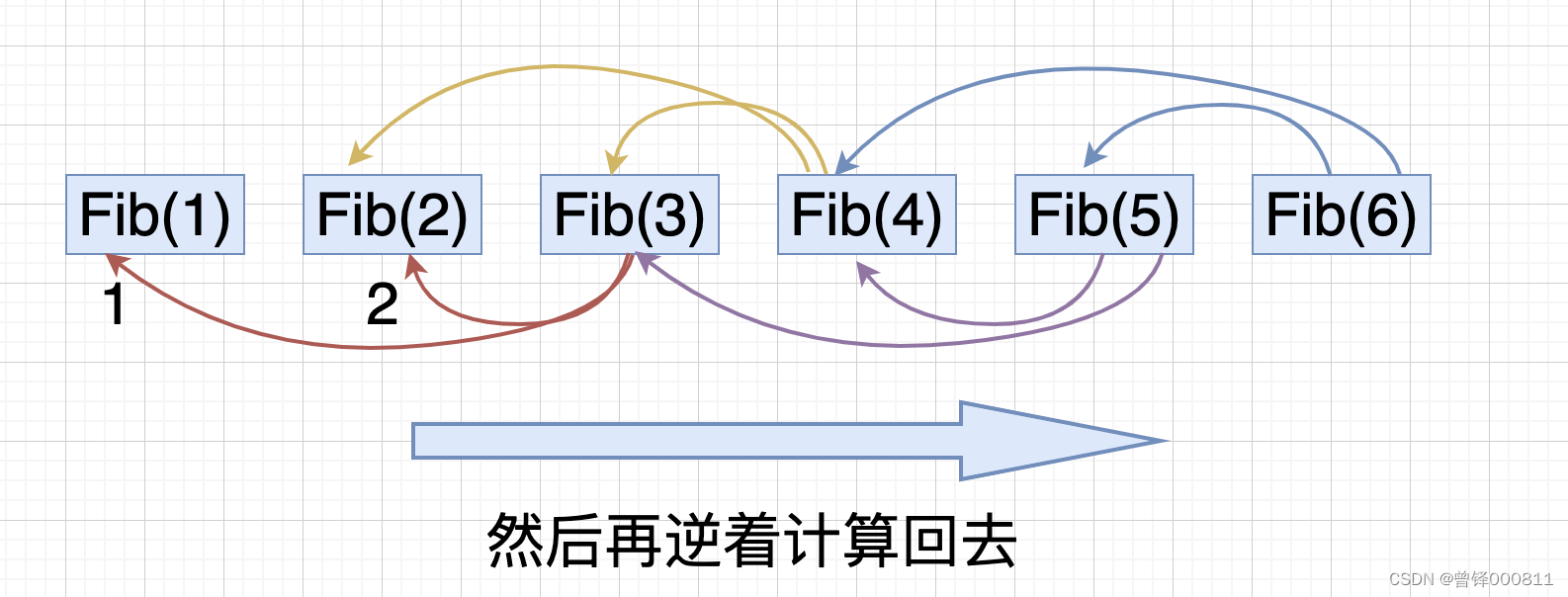
这时程序的时间复杂度就变为了：O（n）
其实重叠子问题（Overlap sub-problem）就是后面动态规划要使用到的思想。
动态规划（Dynamic Programming）：
在王晓东的《算法设计与分析》中，对动态规划是这样介绍的：动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
动态规划算法适用于解最优化问题，通常可以按以下步骤设计动态规划算法：
（1）找出最优解的性质，并刻画其结构特征。
（2）递归地定义最优值
（3）以自底向上的方式计算出最优值
（4）根据计算最优解时得到的信息，构造最优解
我们通过下面两个例子来理解这四个步骤：
动态规划最优解问题：
问题描述：
此时我们要在外面工作赚钱，下图是在不同的时间段工作可以拿到的报酬，例如我们选择工作1可以拿到的报酬是5元，但是在选择了工作1之后因为时间冲突就不能选择工作2或是工作3以此往后类推，我们现在要算出怎么安排今天的工作，能将我们所能获取到的利益进行最大化，求出最优解：
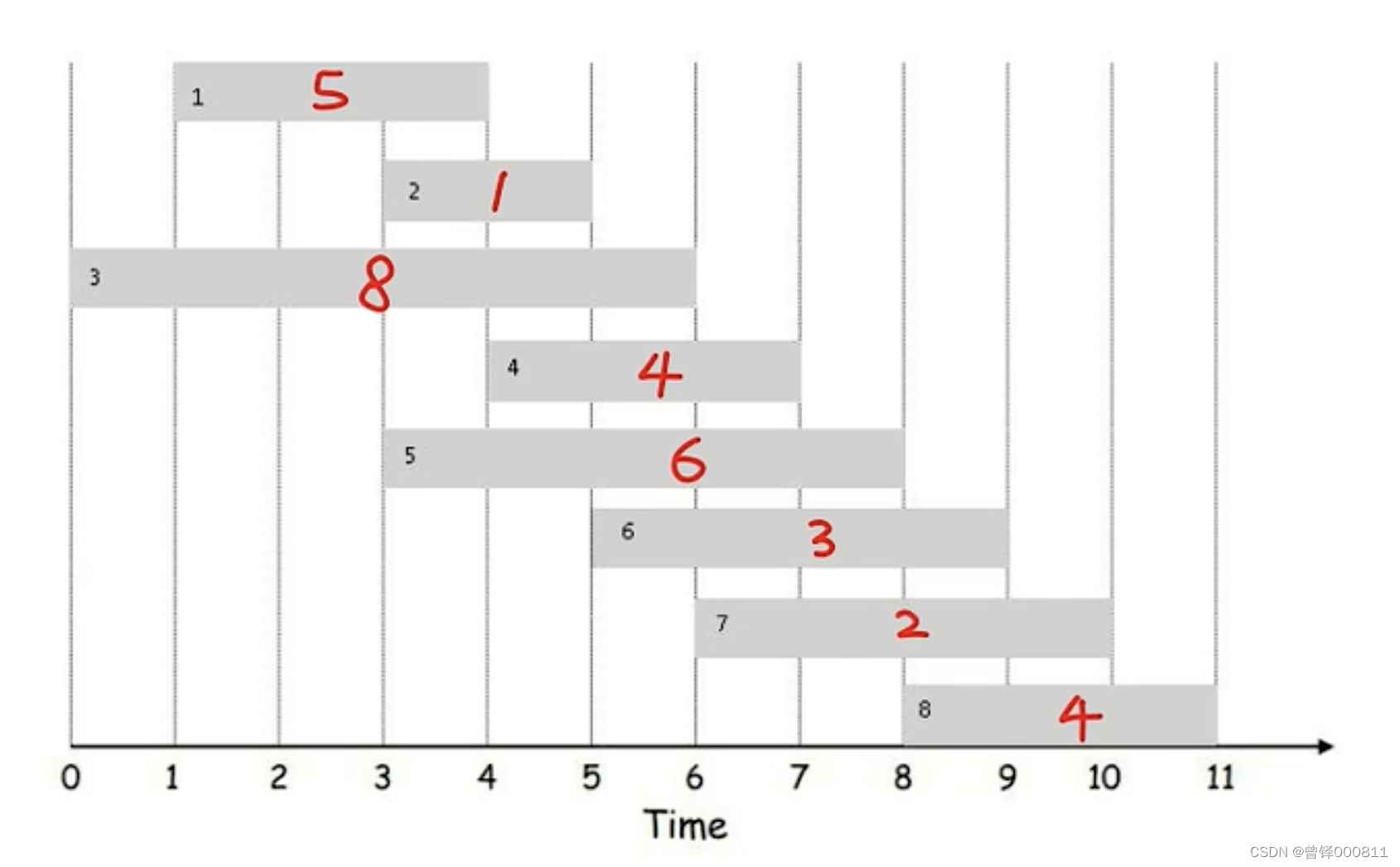
问题分析：
在这个题目中，牵扯到了一个选择问题，就是对于这个时间段的工作的选或不选问题
此时设置三个参量分别是Opt、Prev、V，前两个的意思分别对应着单词optimize(使最优化)和previous（先前的），Opt选择最优值，Prev代表这个选择之前的最优选择，V代表这个选择对应的价值。
这里举一个例子来使我们快速切入：
例如我在这里第一次瞄准工作8，我们就有了两种选择，就是选择工作8和不选工作8，可以这样表示：
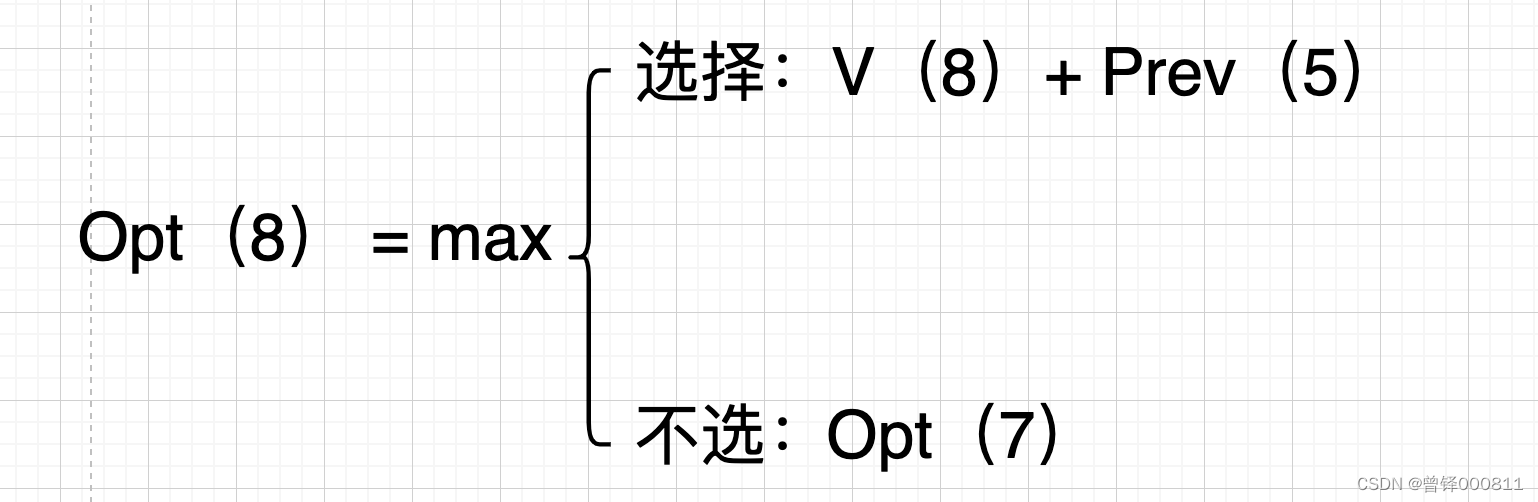
如果我们选择工作8的话，我们就要在前5份工作中找出最优值并加上工作8所能产生的收益，如果不选，我们就直接在前7份工作里面找出最优值。先来画一张图来将Prev和Opt的关系搞清楚：
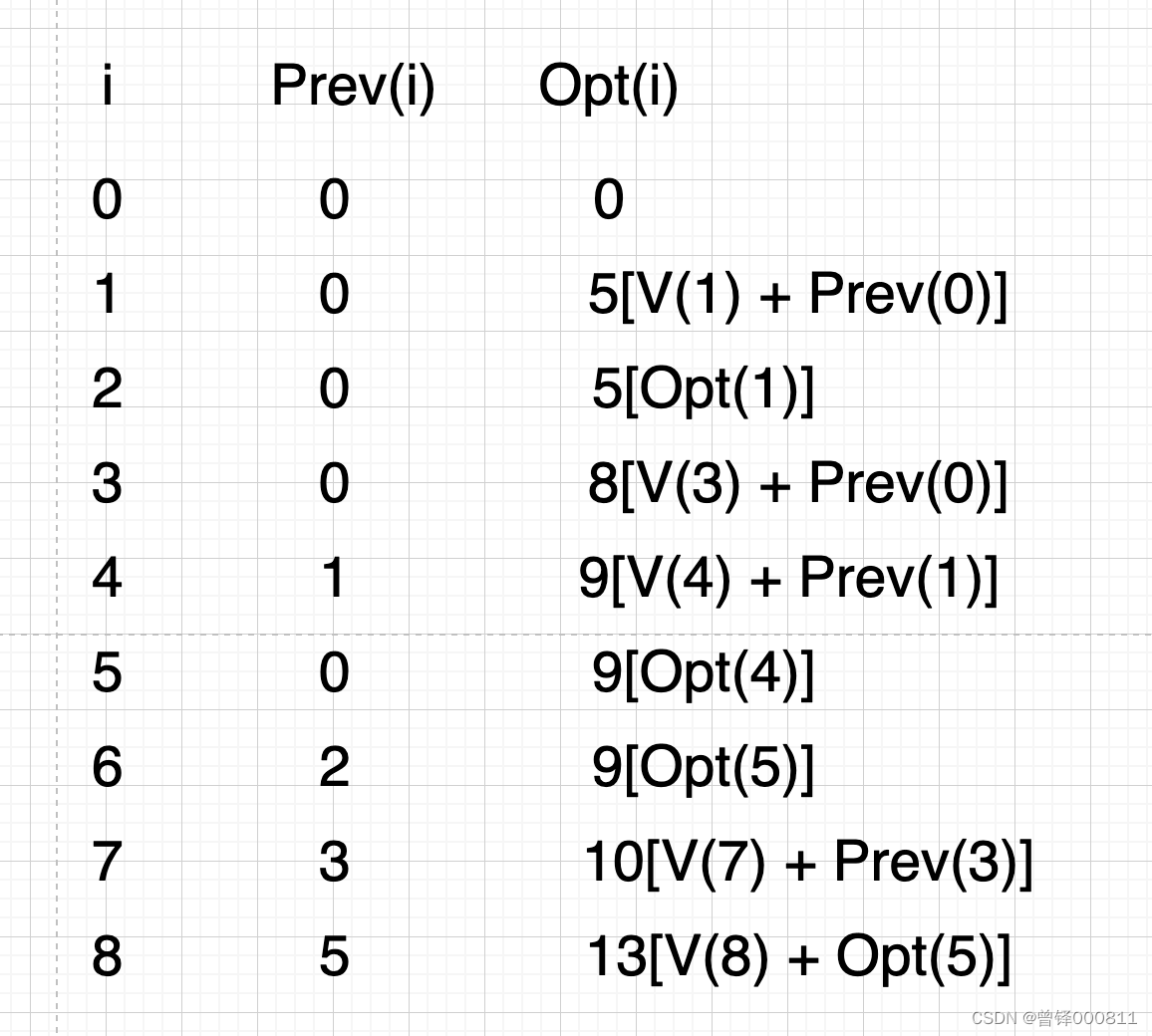
我们这样理解这张图：
当遍历至工作1时，所能产生的最大收益就是只干工作1，收益为5；
当遍历至工作2时，能产生的最大收益就是只干工作2，，收益为1；
当遍历至工作3时，能产生的最大收益就是只干工作3，收益为8；
当遍历至工作4时，能产生的最大收益是既干工作4再干工作1，收益为9；
当遍历至工作5时，能产生的最大收益就是不选工作五而是选择之前遍历至工作4的最优结果，收益为9；
当遍历至工作6时，能产生的最大收益就是不选工作六而是选择之前遍历至工作5的最优结果，收益为9；
当遍历至工作7时，能产生的最大收益就是既选择工作7再干遍历至工作3时最优结果，收益为10；
当遍历至工作8时，所能产生的最大收益就是选择了工作8再干遍历至工作5时的最优结果，在前面说过遍历至工作5的最优结果就是选了工作4再选择工作1，所以就是分别做工作1、工作4、工作8，收益为13；
综上所述，这个问题的最优解就是13。这也就是自底向上求出最优值。
不相邻数字相加和最大问题：
问题描述：
在若干个存放在数组的数字中，我们需要找出彼此不相邻的数字来使她们相加起来的和最大 ，而若干个数字就有若干种选择，例如我在这里给出7个数字均存放在0-6号下标的数组中，分别是：
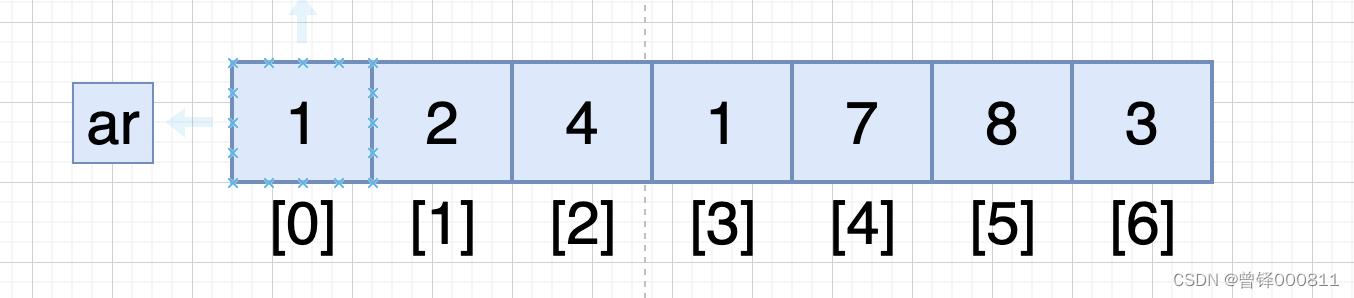
如果我在这时选择了元素4，此时他的不相邻元素就是，0号下标的1元素、4号下标的7元素、6号下标的3元素。
我们现在要做的就是要求这一个序列中所存在的不相邻元素和的最大值，而这取决于我们选择哪一个。
问题分析：
首先我们设置两个形参，分别是OPT，i，i表示第几个元素，OPT用来表示第一个元素到第i个元素的最大和值。
遍历至元素1时，此时i的值为1，也就是OPT（1），因为只有一个元素，所以最优选择只能是1，返回的就是ar[0]本身的值。
遍历至元素2时，此时i的值为2，也就是OPT（2），因为有两个元素，他们还不能相邻，所以要么选第一个要么选第二个，用式子来表达就是：ar[0] > ar[1] ? ar[0] : ar[1];
遍历至元素3时，此时i的值为3，也就是OPT（3）现在我们有两种选择，一种是我们选择元素3，选择元素3之后和元素3不相邻的有元素1，用式子来表达就是: OPT(3) = OPT(1) + ar[2] ；另一种是我们选择元素2，因为元素2没有不相邻的元素，返回的也就是元素2本身的值了，也就是ar[1]；
遍历元素4时，此时i的值为4，也就是OPT（4），现在依然有两种选择，一种是我们选择元素4，与元素4不相邻的元素有2，用式子来表达也就是：OPT(4) = OPT(2) = ar[3]；另一种是我们选择元素4的前一个元素，元素3，此时元素3有一个不相邻的元素时元素1，用式子表达也就是：OPT(3) = OPT(1) + ar[2]；
遍历至元素5时，此时i的值为5，也就是OPT(5)，现在我们如果选择元素5的话，用式子来表达也就是：OPT(5) = OPT(3) + ar[4] , 此时出现了OPT（3），我们之前已经讨论过，这就是重叠子问题（Overlap subproblem），所以我们直接将OPT（3）代入式子即可，所以OPT（5）的值就是12。当我们不选择元素5转而选择5之前的元素4时，这时式子就变成了OPT（4） = OPT(2)+ ar[3]，我们之前也讨论过OPT（2），继续代入，此时OPT（4） = 3; 很明显OPT(5) > OPT(4)，所以此时的最优选择为OPT（5），值为12。
遍历至元素6时，此时i的值为6，同样有两种选择，选择元素6用式子来表达就是：OPT(6) = OPT(4) + ar[5]，如果我们不选择元素6转而选择6之前的元素5，用式子来表达就是OPT(5) = OPT(3) + ar[4],之前已经计算过OPT(5)的值为12，OPT(4)为3，所以OPT(6)的值为3+8=11，OPT(5) > OPT(6),所以此时的最优选择为OPT(5)，值为12。
遍历至元素7时，此时i的值为7，同样有两种选择，选择元素7用式子来表达就是：OPT(7) = OPT(5) + ar[6] , 如果我们不选择元素7转而选择7之前的元素6，用式子来表达就是OPT(6) = OPT(4) + ar[5]，之前已经计算过OPT(6)的值为12，OPT(5)的值为12，所以OPT(7)的值为12 + 3 = 15，OPT (7)>OPT (6)，所以此时的最优选择为OPT(5)，值为15，这也是本题的最终解。
树状图形式分析：
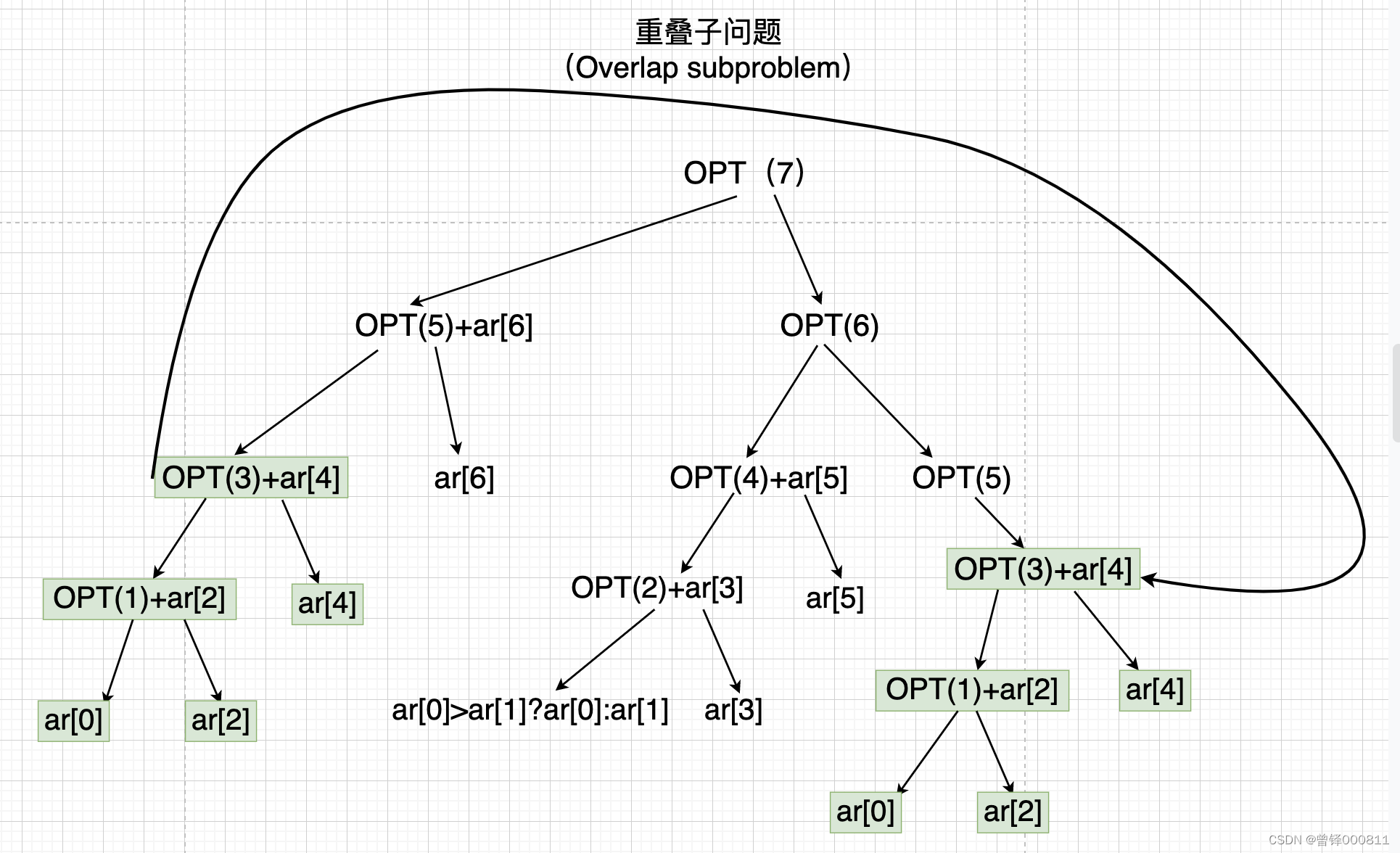
图中绿色方框框住的表达式即是重叠子问题，可以通过记忆功能相互代入以有效的降低递归的时间复杂度。
表格形式分析：
注：蓝色方框对应的是随着遍历元素个数的增加，第一个到遍历到的第i个元素的最大和值。相同的值代表的就是重叠子问题，可以互相代入，以降低程序时间复杂度。
规律总结：
此时分析过程我们已经基本清楚，现在把分析出来的规律写成方程：
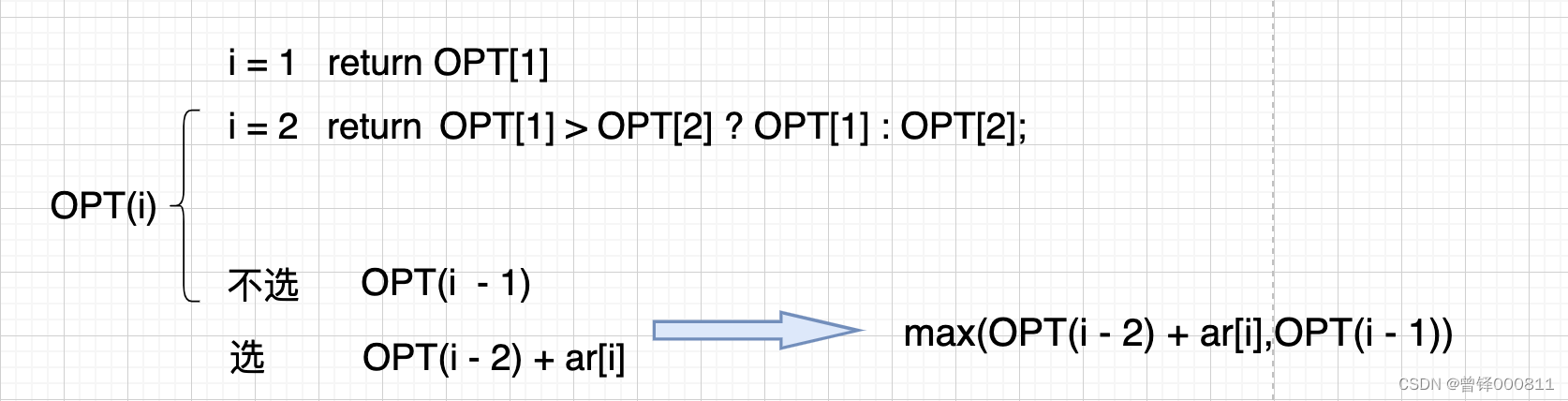
注：OPT(i - 2)和ar[i]中的两个i不一样！前者表示的是第几个元素，后者表示的是数组中元素的下标。
代码实现（递归方法）：
//动态规划（不相邻数字最大和问题）
#include<cstdio>
#include<cassert>
#include<cstdlib>
int Recursion_OPT(int *ar,int i)//递归方法
{
assert(ar != NULL);
if(i == 0){//讨论当选择第一个元素的情况
return ar[0];
}
else if(i == 1){//讨论当选择第二个元素的情况
return ar[0] > ar[1] ? ar[0] : ar[1];
}
else{//讨论其他元素的情况
int a = Recursion_OPT(ar,i - 2) + ar[i];
int b = Recursion_OPT(ar,i - 1);
return a > b ? a : b;//在两种情况中选择最大值
}
}
int main()
{
int ar[7] = {1,2,4,1,7,8,3};
printf("result = %d\n",Recursion_OPT(ar,7));//调用函数
return 0;
}运行结果：
代码实现：动态规划（重叠子问题记忆功能）
//动态规划（不相邻数字最大和问题）
#include<cstdio>
#include<cassert>
#include<cstdlib>
int DP_OPT(int *ar,int i)//动态规划方法（优化重叠子问题方式）
{
int *p = (int *)calloc(7, sizeof(int));//在堆区申请7个int类型的空间并全部初始化为0
if (i == 0) {//当选择第一个元素时，直接返回ar[0]的值
return ar[0];
} else if (i == 1) {//选择第二个元素的值时，返回ar[0]和ar[1]中较大的值
return ar[0] > ar[1] ? ar[0] : ar[1];
}
p[0] = ar[0];//将数组中的值复制给堆区申请的int类型空间（已初始化为0）
p[1] = ar[0] > ar[1] ? ar[0] : ar[1];
for (int j = 2; j <= 6; j++) {//讨论其他元素
int a = p[j - 2] + ar[j];//方程思想
int b = p[j - 1];
p[j] = a > b ? a : b;
}
return p[6];
}
int main()
{
int ar[7] = {1,2,4,1,7,8,3};
printf("result = %d\n",DP_OPT(ar,7));
return 0;
}运行结果：
两种方法的对比：
第一种方法为递归方法，没有很好的利用重叠子问题，空间的代价非常高，时间复杂度为：O（2(^n)）；
第二种方法为动态规划算法，利用了重叠子问题并相互代入，有效地将时间复杂度降为了O(n).
https://www.bilibili.com/video/BV18x411V7fm?spm_id_from=333.880.my_history.page.click&vd_source=c121339fd44664a8ecff62ce46a4724d